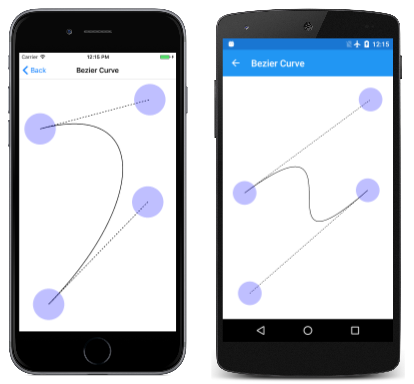
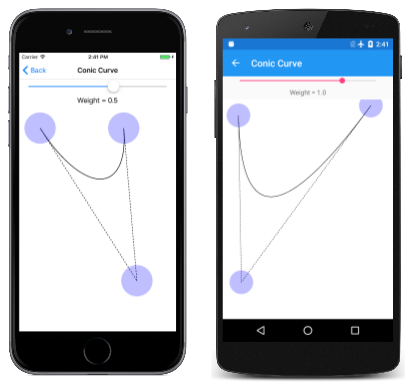
3가지 형식의 Bézier 곡선
SkiaSharp를 사용하여 입방형, 이차 및 원뿔형 베지어 곡선을 렌더링하는 방법 살펴보기
베지어 곡선은 자동차 회사 르노의 프랑스 엔지니어인 피에르 베지어(Pierre Bézier, 1910 – 1999)의 이름을 따서 명명되었으며, 자동차 바디의 컴퓨터 보조 디자인에 곡선을 사용했습니다.
Bézier 곡선은 대화형 디자인에 적합한 것으로 알려져 있습니다. 즉, 곡선이 무한하거나 다루기 힘든 특이점이 없으므로 일반적으로 심미적으로 만족합니다.

컴퓨터 기반 글꼴의 문자 윤곽선은 일반적으로 베지어 곡선으로 정의됩니다.
Bézier 곡선에 대한 Wikipedia 문서에는 몇 가지 유용한 배경 정보가 포함되어 있습니다. 베지어 곡선이라는 용어는 실제로 비슷한 곡선의 패밀리를 나타냅니다. SkiaSharp는 입방형, 이차 및 원뿔형이라고 하는 세 가지 유형의 베지어 곡선을 지원합니다. 원뿔형은 합리적 이차라고도합니다.
입방형 베지어 곡선
입방형은 대부분의 개발자가 베지어 곡선의 주제가 올 때 생각하는 베지어 곡선의 유형입니다.
세 SKPoint 개의 매개 변수가 있는 메서드를 사용하거나 별도의 yx 매개 변수와 매개 변수가 있는 오버로드를 사용하여 CubicTo 개체에 CubicTo 입방형 3차원 곡선 SKPath 을 추가할 수 있습니다.
public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)
public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)
곡선은 윤곽선의 현재 지점에서 시작됩니다. 전체 입방형 베지어 곡선은 4포인트로 정의됩니다.
- 시작점: 윤곽선의 현재 지점 또는 호출되지 않은 경우
MoveTo(0, 0) - 첫 번째 제어점:
point1호출 중CubicTo - 두 번째 제어점:
point2호출 중CubicTo - 끝점:
point3호출 중CubicTo
결과 곡선은 시작점에서 시작하여 끝점에서 끝납니다. 곡선은 일반적으로 두 제어점을 통과하지 않습니다. 대신 제어점은 자석처럼 작동하여 곡선을 향해 당깁니다.
입방형 베지어 곡선에 대한 느낌을 얻는 가장 좋은 방법은 실험입니다. 이는 .에서 InteractivePage파생되는 베지어 곡선 페이지의 용도입니다. BezierCurvePage.xaml 파일은 및 TouchEffect을 SKCanvasView 인스턴스화합니다. BezierCurvePage.xaml.cs 코드 숨김 파일은 생성자에 4개의 TouchPoint 개체를 만듭니다. PaintSurface 이벤트 처리기는 네 개의 TouchPoint 개체를 기반으로 Bézier 곡선을 렌더링하는 방법을 만들고SKPath, 제어점에서 끝점으로 점선이 있는 탄젠트 선을 그립니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[2].Center.X,
touchPoints[2].Center.Y,
touchPoints[3].Center.X,
touchPoints[3].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
여기서 실행 중입니다.
수학적으로 곡선은 입방 다항식입니다. 곡선은 최대 3포인트에서 직선과 교차합니다. 시작점에서 곡선은 항상 시작점에서 첫 번째 제어점까지 직선과 같은 방향으로 탄젠트됩니다. 끝점에서 곡선은 항상 두 번째 제어점에서 끝점까지 직선과 같은 방향으로 탄젠트됩니다.
입방형 베지어 곡선은 항상 4포인트를 연결하는 보행 사분면으로 제한됩니다. 이를 공록 선체라고합니다. 제어점이 시작점과 끝점 사이의 직선에 놓이면 Bézier 곡선이 직선으로 렌더링됩니다. 그러나 세 번째 스크린샷에서 알 수 있듯이 곡선 자체도 교차할 수 있습니다.
경로 윤곽은 여러 개의 연결된 입방형 베지어 곡선을 포함할 수 있지만, 다음 세 점이 콜린어(즉, 직선에 있음)인 경우에만 두 입방형 베지어 곡선 간의 연결이 매끄럽습니다.
- 첫 번째 곡선의 두 번째 제어점
- 첫 번째 곡선의 끝점이며 두 번째 곡선의 시작점이기도 합니다.
- 두 번째 곡선의 첫 번째 제어점
SVG 경로 데이터에 대한 다음 문서에서는 부드러운 연결 Bézier 곡선의 정의를 용이하게 하는 기능을 검색합니다.
입방형 베지어 곡선을 렌더링하는 기본 매개 변수 수식을 아는 것이 유용한 경우도 있습니다. 0에서 1 사이의 t의 경우 매개 변수 수식은 다음과 같습니다.
x(t) = (1 – t)5x + 3t(1 – t)²x + 3t²(1 – t)x
y(t) = (1 – t)5y + 3t(1 – t)²y + 3t²(1 – t)y y 1 + t
3의 가장 높은 지수는 이것이 입방 다항식임을 확인합니다. 0이면 점이 t 시작점인 (x, y)이고 t , 1이면 점이 끝점인 (x, y)임을 쉽게 확인할 수 있습니다. 시작점(낮은 값의 t경우)에 가까우면 첫 번째 제어점(x, y)이 강력한 효과를 발휘하고, 끝점('t'의 높은 값) 근처에 두 번째 제어점(x 으로, y y 은)이 강한 효과를 줍니다.
원형 호에 대한 베지어 곡선 근사치
때로는 베지어 곡선을 사용하여 원호를 렌더링하는 것이 편리합니다. 입방형 베지어 곡선은 원호를 쿼터 원까지 아주 잘 근사화할 수 있으므로 연결된 4개의 베지어 곡선은 전체 원을 정의할 수 있습니다. 이 근사값은 25년 전에 게시된 두 문서에서 설명합니다.
Tor Dokken, et al, "곡률 연속 베지어 곡선에 의한 원의 좋은 근사치", 컴퓨터 보조 기하학적 디자인 7 (1990), 33-41.
마이클 Goldapp, "입방 다항식에 의해 원형 아크의 근사치," 컴퓨터 보조 기하학적 디자인 8 (1991), 227-238.
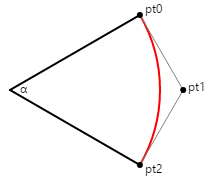
다음 다이어그램은 레이블이 pt1pt2지정된 pto4개의 점과 pt3 원형 호를 근사하는 3차원 곡선(빨간색으로 표시됨)을 정의하는 방법을 보여 줍니다.
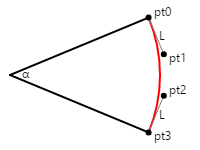
시작점과 끝점에서 제어점에 이르는 선은 원과 베지어 곡선에 대한 탄젠트이며 길이는 L입니다. 위에서 인용한 첫 번째 문서는 길이 L이 다음과 같이 계산되면 베지어 곡선이 원형 호를 가장 잘 근사화한다는 것을 나타냅니다.
L = 4 × tan(α / 4) / 3
이 그림에서는 45도 각도를 보여 주므로 L은 0.265와 같습니다. 코드에서 해당 값은 원의 원하는 반지름을 곱합니다.
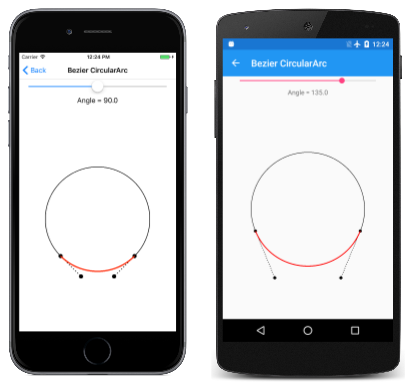
베지어 서큘러 아크 페이지에서는 베지어 곡선을 정의하여 최대 180도까지의 각도에 대한 원호를 근사화할 수 있습니다. BezierCircularArcPage.xaml 파일은 각도를 선택하기 위해 및 a Slider 를 인스턴스화 SKCanvasView 합니다. PaintSurface BezierCircularArgPage.xaml.cs 코드 숨김 파일의 이벤트 처리기는 변환을 사용하여 점(0, 0)을 캔버스의 중심으로 설정합니다. 비교를 위해 해당 지점을 중심으로 원을 그린 다음, Bézier 곡선의 두 제어점을 계산합니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 3;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate length of control point line
float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the end points
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point3 = new SKPoint(radius * sin, radius * cos);
// Find the control points
SKPoint point0Normalized = Normalize(point0);
SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
-length * point0Normalized.X);
SKPoint point3Normalized = Normalize(point3);
SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
length * point3Normalized.X);
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);
// Draw the Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.CubicTo(point1, point2, point3);
canvas.DrawPath(path, redStroke);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
시작점과 끝점(point0 및 point3)은 원에 대한 일반적인 매개 변수 수식을 기반으로 계산됩니다. 원은 (0, 0) 가운데에 있기 때문에 이러한 점들은 원의 중심에서 둘레까지 방사형 벡터로 처리될 수도 있습니다. 제어점은 원에 탄젠트된 선에 있으므로 이러한 방사형 벡터에 대한 직각입니다. 다른 벡터에 대한 직각의 벡터는 단순히 X 및 Y 좌표가 교환된 원래 벡터이며 그 중 하나는 음수로 만들어집니다.
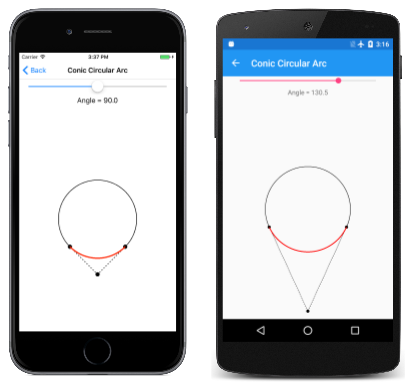
다양한 각도로 실행되는 프로그램은 다음과 같습니다.
세 번째 스크린샷을 자세히 살펴보면 각도가 180도일 때 베지어 곡선이 반원에서 벗어나는 것을 볼 수 있지만, iOS 화면에는 각도가 90도일 때 쿼터 서클에 잘 맞는 것으로 보입니다.
쿼터 원이 다음과 같이 방향을 지정하면 두 제어점의 좌표를 계산하는 것이 매우 쉽습니다.
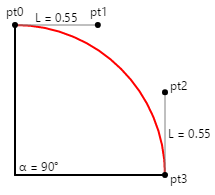
원의 반경이 100 이면 L 은 55이고 기억하기 쉬운 숫자입니다.
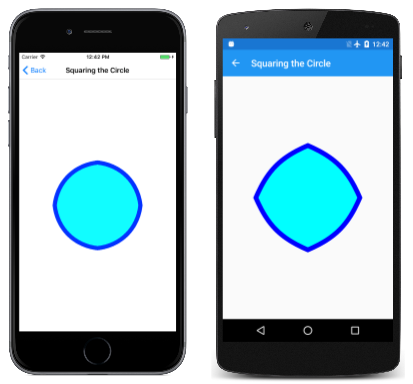
원 제곱 페이지는 원과 정사각형 사이의 그림에 애니메이션 효과를 낸다. 원은 클래스에서 이 배열 정의 SquaringTheCirclePage 의 첫 번째 열에 좌표가 표시되는 4개의 베지어 곡선으로 근사치입니다.
public class SquaringTheCirclePage : ContentPage
{
SKPoint[,] points =
{
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() },
{ new SKPoint( 55, 100), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 55), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 0), new SKPoint( 125, 0), new SKPoint() },
{ new SKPoint( 100, -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 0, -100), new SKPoint( 0, -125), new SKPoint() },
{ new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, 0), new SKPoint( -125, 0), new SKPoint() },
{ new SKPoint(-100, 55), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( -55, 100), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() }
};
...
}
두 번째 열에는 영역이 원 영역과 거의 같은 사각형을 정의하는 네 개의 베지어 곡선의 좌표가 포함됩니다. (지정된 원과 같은 정확한 영역으로 사각형을 그리는 것은 원을 제곱하는 클래식에서 해결할 수 없는 기하학적 문제입니다.) 베지어 곡선으로 사각형을 렌더링하는 경우 각 곡선의 두 제어점은 동일하며 시작점과 끝점이 있는 콜린어이므로 Bézier 곡선은 직선으로 렌더링됩니다.
배열의 세 번째 열은 애니메이션의 보간된 값에 대한 것입니다. 이 페이지는 타이머를 16밀리초로 설정하고 처리기는 해당 속도로 호출됩니다 PaintSurface .
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));
// Interpolate
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 3 / 3); // 0 to 1 every 3 seconds
t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2; // 0 to 1 to 0 sinusoidally
for (int i = 0; i < 13; i++)
{
points[i, 2] = new SKPoint(
(1 - t) * points[i, 0].X + t * points[i, 1].X,
(1 - t) * points[i, 0].Y + t * points[i, 1].Y);
}
// Create the path and draw it
using (SKPath path = new SKPath())
{
path.MoveTo(points[0, 2]);
for (int i = 1; i < 13; i += 3)
{
path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
}
path.Close();
canvas.DrawPath(path, cyanFill);
canvas.DrawPath(path, blueStroke);
}
}
점이 부비동으로 진동하는 값을 t기준으로 보간됩니다. 보간된 점들은 연결된 4개의 베지어 곡선을 구성하는 데 사용됩니다. 실행 중인 애니메이션은 다음과 같습니다.
이러한 애니메이션은 원형 호와 직선으로 렌더링될 수 있을 만큼 알고리즘적으로 유연한 곡선이 없으면 불가능합니다.
또한 베지어 무한대 페이지는 베지어 곡선의 기능을 활용하여 원호를 근사화합니다. 클래스의 PaintSurface 처리기는 BezierInfinityPage 다음과 같습니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.MoveTo(0, 0); // Center
path.CubicTo( 50, -50, 95, -100, 150, -100); // To top of right loop
path.CubicTo( 205, -100, 250, -55, 250, 0); // To far right of right loop
path.CubicTo( 250, 55, 205, 100, 150, 100); // To bottom of right loop
path.CubicTo( 95, 100, 50, 50, 0, 0); // Back to center
path.CubicTo( -50, -50, -95, -100, -150, -100); // To top of left loop
path.CubicTo(-205, -100, -250, -55, -250, 0); // To far left of left loop
path.CubicTo(-250, 55, -205, 100, -150, 100); // To bottom of left loop
path.CubicTo( -95, 100, -50, 50, 0, 0); // Back to center
path.Close();
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
그래프 용지에 이러한 좌표를 그리는 것이 좋은 연습일 수 있습니다. 무한대 기호는 점(0, 0)을 중심으로 하며, 두 루프의 중심은 (-150, 0) 및 (150, 0) 및 반경 100입니다. 일련의 CubicTo 명령에서 –95 및 –205의 값을 사용하는 제어점의 X 좌표(해당 값은 -150 더하기 및 마이너스 55), 205 및 95(150 plus 및 minus 55), 오른쪽 및 왼쪽의 경우 250 및 –250을 볼 수 있습니다. 유일한 예외는 무한대 기호가 가운데에서 교차하는 경우입니다. 이 경우 제어점에는 50과 –50의 조합으로 좌표가 있으므로 중심 근처의 곡선을 곧게 펴야 합니다.
무한대 기호는 다음과 같습니다.
Arc를 그리는 세 가지 방법 문서에서 Arc Infinity 페이지에서 렌더링한 무한대 기호보다 중앙으로 다소 매끄럽습니다.
4차원 베지어 곡선
4차원 3차원 곡선에는 제어점이 하나뿐이며, 곡선은 시작점, 제어점 및 끝점의 세 가지 지점으로 정의됩니다. 파라메트릭 수식은 가장 높은 지수가 2라는 점을 제외하고 입방형 베지어 곡선과 매우 유사하므로 곡선은 이차 다항식입니다.
x(t) = (1 – t)²x + 2t(1 – t)x + t²x
y(t) = (1 – t)²y + 2t(1 – t)y + t²y
경로에 이차 Bézier 곡선을 추가하려면 별도의 좌표와 y 함께 x 메서드 또는 QuadTo 오버로드를 사용합니다QuadTo.
public void QuadTo (SKPoint point1, SKPoint point2)
public void QuadTo (Single x1, Single y1, Single x2, Single y2)
메서드는 현재 위치에서 제어점으로 커 point1 브를 point2 추가합니다.
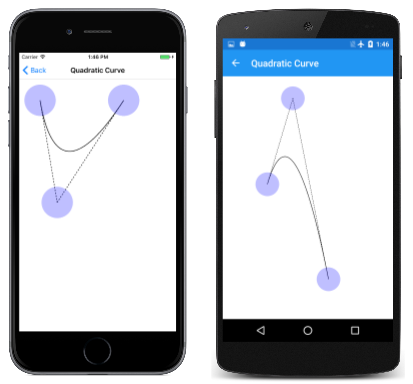
3개의 터치 포인트만 있는 것을 제외하고는 베지어 곡선 페이지와 매우 유사한 4차원 곡선 페이지를 사용하여 4차원 베지어 곡선을 실험할 수 있습니다. QuadraticCurve.xaml.cs 코드 숨김 파일의 PaintSurface처리기는 다음과 같습니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with quadratic Bezier
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.QuadTo(touchPoints[1].Center,
touchPoints[2].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
여기서는 다음을 실행합니다.
점선은 시작점 및 끝점의 곡선에 탄젠트되고 제어점에서 충족됩니다.
일반 도형의 곡선이 필요한 경우 이차 베지어는 좋지만 두 개보다는 하나의 제어점만 사용하는 것이 좋습니다. 이차 베지어는 다른 곡선보다 더 효율적으로 렌더링되므로 Skia에서 내부적으로 타원형 호를 렌더링하는 데 사용됩니다.
그러나 이차 베지어 곡선의 모양은 타원형이 아니기 때문에 타원형 호를 근사화하기 위해 여러 이차 베지어가 필요합니다. 이차 베지어는 대신 포물선의 세그먼트입니다.
코닉 베지어 곡선
합리적 이차 베지어 곡선이라고도 하는 원뿔형 베지어 곡선은 베지어 곡선 제품군에 비교적 최근에 추가된 곡선입니다. 이차 베지어 곡선과 마찬가지로 합리적인 이차 베지어 곡선에는 시작점, 끝점 및 하나의 제어점이 포함됩니다. 그러나 합리적인 이차 베지어 곡선에도 가중치 값이 필요합니다. 파라메트릭 수식에는 비율이 포함되기 때문에 합리적 이차라고 합니다.
X 및 Y에 대한 매개 변수 수식은 동일한 분모를 공유하는 비율입니다. 다음은 0에서 1 사이의 t에 대한 분모의 수식과 w의 가중치 값입니다.
d(t) = (1 – t)² + 2wt(1 – t) + t²
이론적으로 합리적 이차에는 세 개의 개별 가중치 값이 포함될 수 있으며, 이 값은 세 개의 용어 각각에 대해 하나씩 포함될 수 있지만 중간 기간에는 하나의 가중치 값으로 단순화할 수 있습니다.
X 및 Y 좌표에 대한 매개 변수 수식은 중간 용어에 가중치 값도 포함하고 식을 분모로 나눈다는 점을 제외하고 이차 베지에 대한 매개 변수 수식과 유사합니다.
x(t) = ((1 – t)²x + 2wt(1 – t)x + t² ÷x
y(t) = ((1 – t)²y + 2wt(1 – t)y + t²y)) ÷ d(t)
합리적 이차 베지어 곡선은 하이퍼볼라, 포물선, 줄임표 및 원과 같은 원뿔형 섹션의 세그먼트를 정확하게 나타낼 수 있기 때문에 원뿔형이라고도 합니다.
경로에 합리적 이차 Bézier 곡선을 추가하려면 메서드 또는 ConicTo 오버로드를 별도의 x 좌표와 y 함께 사용합니다ConicTo.
public void ConicTo (SKPoint point1, SKPoint point2, Single weight)
public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)
최종 weight 매개 변수를 확인합니다.
원뿔형 곡선 페이지에서 이러한 곡선을 실험할 수 있습니다. ConicCurvePage 클래스는 InteractivePage에서 파생됩니다. ConicCurvePage.xaml 파일은 –2에서 2 사이의 가중치 값을 선택하도록 인스턴스화 Slider 합니다. ConicCurvePage.xaml.cs 코드 숨김 파일은 세 개의 TouchPoint 개체를 만들고 처리 PaintSurface 기는 단순히 탄젠트 선을 사용하여 결과 곡선을 제어점에 렌더링합니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with conic curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ConicTo(touchPoints[1].Center,
touchPoints[2].Center,
(float)weightSlider.Value);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
여기서 실행 중입니다.
당신이 볼 수 있듯이, 제어점은 무게가 높을 때 더 그것을 향해 곡선을 당기는 것 같다. 가중치가 0이면 곡선이 시작점에서 끝점까지 직선이 됩니다.
이론적으로 음수 가중치가 허용되고 곡선이 제어점에서 멀리 구부러집니다. 그러나 가중치가 –1 이하이면 매개 변수 수식의 분모가 t의 특정 값에 대해 음수가 됩니다. 이러한 이유로 음수 가중치는 메서드에서 ConicTo 무시됩니다. 원뿔형 곡선 프로그램을 사용하면 음수 가중치를 설정할 수 있지만 실험에서 볼 수 있듯이 음의 가중치는 가중치 0과 동일한 효과를 가지며 직선이 렌더링됩니다.
제어점과 가중치를 파생하는 것은 반원까지 원호를 그리는 방법을 사용하는 ConicTo 것이 매우 쉽습니다(포함 안 됨). 다음 다이어그램에서는 시작점과 끝점의 탄젠트 선이 제어점에서 만난다.
삼각을 사용하여 원의 중심에서 제어점의 거리를 확인할 수 있습니다. 원의 반경은 α 각도의 절반 코사인으로 나뉩니다. 시작점과 끝점 사이에 원호를 그리려면 가중치를 각도의 절반인 동일한 코사인으로 설정합니다. 각도가 180도이면 탄젠트 선이 충족되지 않으며 무게는 0입니다. 그러나 180도 미만의 각도의 경우 수학이 잘 작동합니다.
원뿔형 원형 호 페이지에서 이를 보여 줍니다. ConicCircularArc.xaml 파일은 각도를 선택하기 위해 인스턴스화합니다Slider. PaintSurface ConicCircularArc.xaml.cs 코드 숨김 파일의 처리기는 제어점과 가중치를 계산합니다.
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 4;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the points and weight
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point1 = new SKPoint(0, radius / cos);
SKPoint point2 = new SKPoint(radius * sin, radius * cos);
float weight = cos;
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);
// Draw the conic
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.ConicTo(point1, point2, weight);
canvas.DrawPath(path, redStroke);
}
}
볼 수 있듯이 빨간색으로 표시된 경로와 참조를 위해 표시되는 기본 원 사이에 ConicTo 는 시각적 차이가 없습니다.
그러나 각도를 180도로 설정하면 수학이 실패합니다.
이론상(매개 변수 수식 기반)에서 원이 동일한 점과 가중치의 음수 값을 사용하여 다른 호출 ConicTo 로 완료될 수 있기 때문에 음수 가중치를 지원하지 않는 것은 불행한 ConicTo 일입니다. 이렇게 하면 0도와 180도 사이의 각도에 따라 두 개의 ConicTo 곡선으로 전체 원을 만들 수 있습니다.