변환에 대한 매트릭스 표현
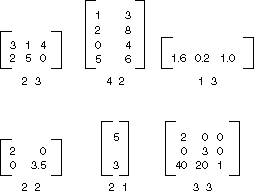
m×n 행렬은 m개 행과 n개 열로 정렬된 숫자 집합입니다. 다음 그림에서는 여러 행렬을 보여줍니다.
개별 요소를 추가하여 동일한 크기의 두 행렬을 추가할 수 있습니다. 다음 그림에서는 행렬 추가의 두 가지 예를 보여줍니다.
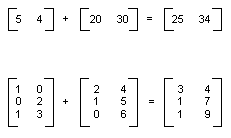
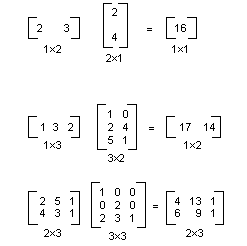
m×n 행렬을 n×p 행렬로 곱할 수 있으며, 결과는 m×p 행렬입니다. 첫 번째 행렬의 열 수는 두 번째 행렬의 행 수와 같아야 합니다. 예를 들어, 4×2 행렬을 2×3 행렬을 곱하여 4×3 행렬을 생성할 수 있습니다.
평면의 점과 행렬의 행과 열을 벡터로 생각할 수 있습니다. 예를 들어, (2, 5)는 두 개의 구성 요소가 있는 벡터이고 (3, 7, 1)은 세 개의 구성 요소가 있는 벡터입니다. 두 벡터의 점 곱은 다음과 같이 정의됩니다.
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
예를 들어, (2, 3) 및 (5, 4)의 점 곱은 (2)(5) + (3)(4) = 22입니다. (2, 5, 1) 및 (4, 3, 1)의 점 곱은 (2)(4) + (5)(3) + (1)(1) = 24입니다. 두 벡터의 점 곱은 다른 벡터가 아닌 숫자입니다. 또한 두 벡터의 구성 요소 수가 동일한 경우에만 점 제품을 계산할 수 있습니다.
A(i, j)가 행렬 A의 i번째 행과 j번째 열에 있는 항목이 되도록 합니다. 예를 들어, A(3, 2)는 행렬 A에서 세 번째 행과 두 번째 열에 있는 항목입니다. A, B 및 C가 행렬이고 AB = C라고 가정합니다. C의 항목은 다음과 같이 계산됩니다.
C(i, j) = (A의 행 i) • (B의 열 j)
다음 그림에서는 행렬 곱하기의 몇 가지 예를 보여줍니다.
평면의 점을 1×2 행렬로 생각하면 해당 점을 2×2 행렬에 곱하여 점을 변환할 수 있습니다. 다음 그림에서는 점(2, 1)에 적용된 여러 변환을 보여줍니다.
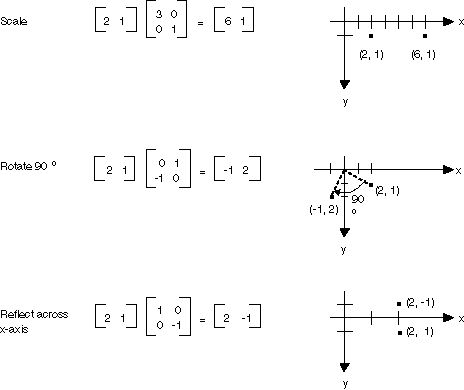
앞의 그림에 표시된 모든 변환은 선형 변환입니다. 이동과 같은 특정 다른 변환은 선형이 아니며, 2×2 행렬을 곱한 것으로 표현할 수 없습니다. 점(2, 1)으로 시작하고, 90도 회전하고, x 방향으로 3단위를 이동하고, y 방향으로 4단위를 이동하려는 경우를 가정해 보겠습니다. 행렬 곱하기와 행렬 더하기를 차례로 사용하여 이 작업을 수행할 수 있습니다.
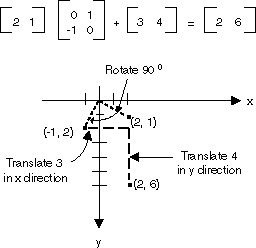
선형 변환(2×2 행렬 곱하기) 후 이동(1×2 행렬 더하기)을 아핀 변환이라고 합니다. 행렬 쌍(선형 파트용 하나와 이동용 하나)에 아핀 변환을 저장하는 방법이 대체는 전체 변환을 3×3 행렬에 저장하는 것입니다. 이 작업을 수행하려면 평면의 점이 더미 3번째 좌표가 있는 1×3 행렬에 저장되어야 합니다. 일반적인 기술은 모든 세 번째 좌표를 1이 되도록 하는 것입니다. 예를 들어 점(2, 1)은 행렬 [2 1 1]로 표시됩니다. 다음 그림에서는 단일 3×3 행렬로 곱하기로 표현된 아핀 변환(90도 회전, x 방향으로 3단위, y 방향으로 4단위 이동)을 보여줍니다.
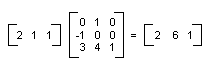
앞의 예제에서 점(2, 1)은 점(2, 6)에 매핑됩니다. 3×3 행렬의 세 번째 열에는 0, 0, 1의 숫자가 포함됩니다. 이것은 항상 아핀 변환의 3×3 행렬에 대한 경우입니다. 중요한 숫자는 열 1과 2의 6개 숫자입니다. 행렬의 왼쪽 위 2×2 부분은 변환의 선형 부분을 나타내고, 세 번째 행의 처음 두 항목은 이동을 나타냅니다.
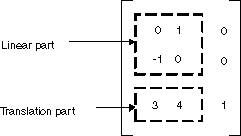
GDI+에서는 아핀 변환을 Matrix 개체에 저장할 수 있습니다. 아핀 변환을 나타내는 행렬의 세 번째 열은 항상 (0, 0, 1)이므로, Matrix 개체를 생성할 때 처음 두 열의 6개 숫자만 지정합니다. Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) 문은 선행 그림에 표시된 행렬을 생성합니다.
복합 변형
복합 변환은 변환 시퀀스이며, 순서대로 되어 있습니다. 다음 목록의 행렬 및 변환을 고려합니다.
| 행렬 | 변환 |
|---|---|
| 행렬 A | 90도 회전 |
| 행렬 B | x 방향에서 2 배율로 크기 조정 |
| 행렬 C | y 방향으로 3단위 이동 |
행렬 [2 1 1]로 표시되는 점 (2, 1)로 시작하고 A, B, C를 순서대로 곱하면 점 (2, 1)이 나열된 순서대로 세 가지 변환을 거칩니다.
[2 1 1]ABC = [-2 5 1]
복합 변환의 세 부분을 별도의 세 행렬에 저장하는 대신, A, B 및 C를 함께 곱하여 전체 복합 변환을 저장하는 단일 3×3 행렬을 가져올 수 있습니다. ABC = D라고 가정합니다. 그런 다음 D를 곱한 점은 A, B, C를 곱한 점과 동일한 결과를 제공합니다.
[2 1 1]D = [-2 5 1]
다음 그림에서는 행렬 A, B, C 및 D를 보여줍니다.
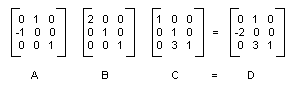
복합 변환의 행렬이 개별 변환 행렬을 곱하여 형성될 수 있다는 사실은 모든 아핀 변환 시퀀스를 단일 Matrix 개체에 저장할 수 있음을 의미합니다.
주의
복합 변환의 순서는 중요합니다. 일반적으로, 회전, 스케일링, 이동 순서는 스케일링, 회전, 이동 순서와 같지 않습니다. 마찬가지로, 행렬 곱하기 순서도 중요합니다. 일반적으로 ABC는 BAC와 동일하지 않습니다.
Matrix 클래스는 복합 변환을 빌드하기 위한 여러 메서드, Multiply, Rotate, RotateAt, Scale, Shear 및 Translate를 제공합니다. 다음 예제에서는 먼저 30도 회전한 다음, y 방향으로 배율 2로 스케일링한 다음, x 방향으로 5 단위를 이동하는 복합 변환의 행렬을 만듭니다.
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
다음 그림은 행렬을 보여줍니다.

참고 항목
.NET Desktop feedback
