자습서: Q#에서 양자 난수 생성기 구현

아티클
01/13/2025

이 자습서에서는 양자 역학의 특성을 활용하여 난수를 생성하는 기본 양자 프로그램을 Q# 작성하는 방법을 알아봅니다.

이 자습서에서는 다음을 수행합니다.

프로그램을 만듭니다 Q# .
프로그램의 주요 구성 요소를 검토합니다 Q# .
문제의 논리를 정의합니다.
클래식 연산과 양자 연산을 결합하여 문제를 해결합니다.
큐빗 및 중첩을 사용하여 양자 난수 생성기를 빌드합니다.

팁

양자 컴퓨팅 과정을 가속화하려면 Azure Quantum 웹 사이트의 고유한 기능인 Azure Quantum을 사용하여 코드를 확인하세요. 여기서는 기본 제공 Q# 샘플 또는 사용자 고유 Q# 의 프로그램을 실행하고, 프롬프트에서 새 Q# 코드를 생성하고, 한 번의 클릭으로 웹용 VS Code에서 코드를 열고 실행하고, Copilot에게 양자 컴퓨팅에 대한 질문을 할 수 있습니다.

필수 조건

Azure Quantum의 Copilot에서 코드 샘플을 실행하려면 다음을 수행합니다.
- Microsoft(MSA) 전자 메일 계정입니다.
Visual Studio Code에서 코드 샘플을 개발하고 실행하려면 다음을 수행합니다.
- 최신 버전의 Visual Studio Code 또는 웹에서 VS Code를 엽니다.
- Azure Quantum Development Kit 확장의 최신 버전입니다. 설치 세부 정보는 QDK 확장설정을 참조하세요.
- Jupyter Notebook을 사용하려면 Pythonqsharp해야 합니다. 이렇게 하려면 터미널을 열고 다음 명령을 실행합니다.
```
$ pip install --upgrade  qsharp
```

문제 정의

일반 컴퓨터에서는 난수가 아니라 의사 난수를 생성합니다. 의사 난수 생성기는 시드라고 하는 일부 초기값을 기준으로 결정적 숫자 시퀀스를 생성합니다. 임의 값을 보다 정확하게 근사하기 위해 이 시드는 CPU 클록의 현재 시간인 경우가 많습니다.

반면에 양자 컴퓨터는 진정한 난수를 생성할 수 있습니다. 이는 중첩된 큐비트 측정이 확률론적 과정이기 때문입니다. 측정 결과는 임의이며 결과를 예측할 수 있는 방법이 없습니다. 이것이 양자 난수 생성기의 기본 원칙입니다.

큐비트는 중첩에 있을 수 있는 양자 정보의 단위입니다. 측정할 때 큐비트는 0 상태 또는 1 상태일 수 있습니다. 하지만 측정 전 큐비트 상태는 측정값이 0 또는 1일 수 있는 확률을 나타냅니다.

먼저 기저 상태(예: 0)의 큐비트로 시작합니다. 난수 생성기의 첫 번째 단계는 Hadamard 연산을 사용하여 큐비트를 동일한 중첩에 배치하는 것입니다. 이 상태를 측정하면 각 결과의 확률이 50%인 0 또는 1이 실제로 임의 비트가 됩니다.

중첩에서 큐비트를 측정한 후에 얻을 수 있는 것을 알 수 있는 방법은 없으며, 결과는 코드가 호출될 때마다 다른 값입니다. 하지만 이 동작을 사용하여 더 큰 난수를 생성하려면 어떻게 해야 하나요?

프로세스를 4번 반복하여 다음과 같은 이진수 시퀀스를 생성한다고 가정하겠습니다.

$${0, 1, 1, 0}$$

이러한 비트를 비트 문자열로 연결하거나 결합하면 더 큰 숫자를 형성할 수 있습니다. 이 예제에서 비트 시퀀스 ${0110}$는 10진수 6과 같습니다.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

이 프로세스를 여러 번 반복하면 여러 비트를 결합하여 큰 숫자를 구성할 수 있습니다. 이 방법을 사용하면 해커가 측정 시퀀스의 결과를 확인할 수 없도록 할 수 있으므로 보안 암호로 사용할 숫자를 만들 수 있습니다.

난수 생성기 논리 정의

난수 생성기의 논리를 간략하게 설명해 보겠습니다.

max를 생성하려는 최대 수로 정의합니다.
생성해야 하는 임의 비트의 수를 정의합니다. 이 작업은 비트 수를 계산하여 수행됩니다. nBits정수를 최대 max로 표현해야 합니다.
길이가 nBits인 임의 비트 문자열을 생성합니다.
비트 문자열이 max보다 큰 숫자를 나타내는 경우 3단계로 돌아갑니다.
그렇지 않으면 프로세스가 완료된 것입니다. 생성된 숫자를 정수로 반환합니다.

예를 들어 max를 12로 설정하겠습니다. 즉, 12는 암호로 사용하려는 가장 큰 숫자입니다.

0에서 12 사이의 숫자를 나타내려면 ${\lfloor ln(12) / ln(2) + 1 \rfloor}$, 즉 4비트가 필요합니다. 모든 정수를 사용하고 이를 나타내는 데 필요한 비트 수를 반환하는 기본 제공 함수 BitSizeI를 사용할 수 있습니다.

${13_{\ decimal}}$에 해당하는 비트 문자열 ${1101_{\ binary}}$를 생성한다고 가정하겠습니다. 13은 12보다 크므로 프로세스를 반복합니다.

다음으로 ${6_{\ decimal}}$에 해당하는 비트 문자열 ${0110_{\ binary}}$를 생성합니다. 6은 12보다 작으므로 프로세스는 완료된 것입니다.

양자 난수 생성기는 숫자 6을 암호로 반환합니다. 적은 수의 값은 가능한 모든 암호를 시도하여 쉽게 해독할 수 있기 때문에 실제로는 더 큰 숫자를 최댓값으로 설정합니다. 실제로 암호 추측 또는 해독을 어렵게 하기 위해 ASCII 코드를 사용하여 이진을 텍스트로 변환하고 숫자, 기호, 대/소문자를 사용하여 암호를 생성할 수 있습니다.

임의 비트 생성기 작성

첫 번째 단계는 임의 Q# 비트를 생성하는 작업을 작성하는 것입니다. 이 작업은 난수 생성기의 구성 요소 중 하나가 됩니다.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

이제 새 코드를 살펴보겠습니다.

입력을 GenerateRandomBit 사용하지 않고 형식 Result값을 생성하는 작업을 정의합니다. Result 형식은 측정 결과를 나타내며 두 가지 가능한 값은 Zero 또는 One입니다.
키워드를 사용하여 단일 큐비트를 할당합니다 use . 할당되면 큐비트는 항상 |0> 상태입니다.
이 H 작업을 사용하여 큐비트를 동일한 중첩에 배치합니다.
이 연산을 M 사용하여 큐비트를 측정하고 측정된 값(Zero 또는 One)을 반환합니다.
이 Reset 작업을 사용하여 큐비트를 |0> 상태로 다시 설정합니다.

H 연산을 사용하여 큐비트를 중첩 상태로 전환하고 M 연산으로 측정하면 코드가 호출될 때마다 다른 결과 값이 반환됩니다.

블로흐 구를 사용하여 코드 시각화 Q#

블로흐 구에서 북극은 클래식 값 0 을 나타내고 남극은 고전 값 1을 나타냅니다. 모든 중첩은 구의 점(화살표로 표시됨)으로 나타낼 수 있습니다. 화살표의 끝이 극에 가까울수록 측정 시 큐비트가 해당 극에 할당된 클래식 값으로 축소할 확률이 높습니다. 예를 들어 다음 그림에서 빨간색 화살표로 표현되는 큐비트 상태는 측정될 경우 0 값을 제공할 확률이 높습니다.

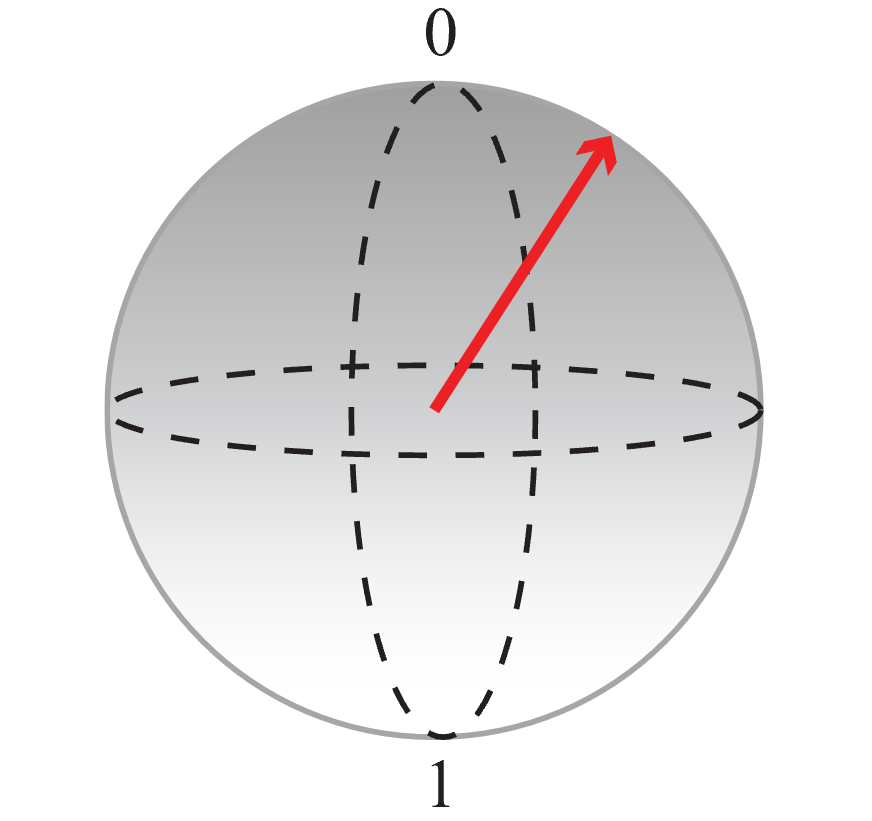
이 표현을 사용하여 코드가 하는 일을 시각화할 수 있습니다.

먼저 |0> 상태에서 초기화된 큐비트로 시작하고 작업을 적용 H 하여 0과 1의 확률이 같은 중첩을 만듭니다.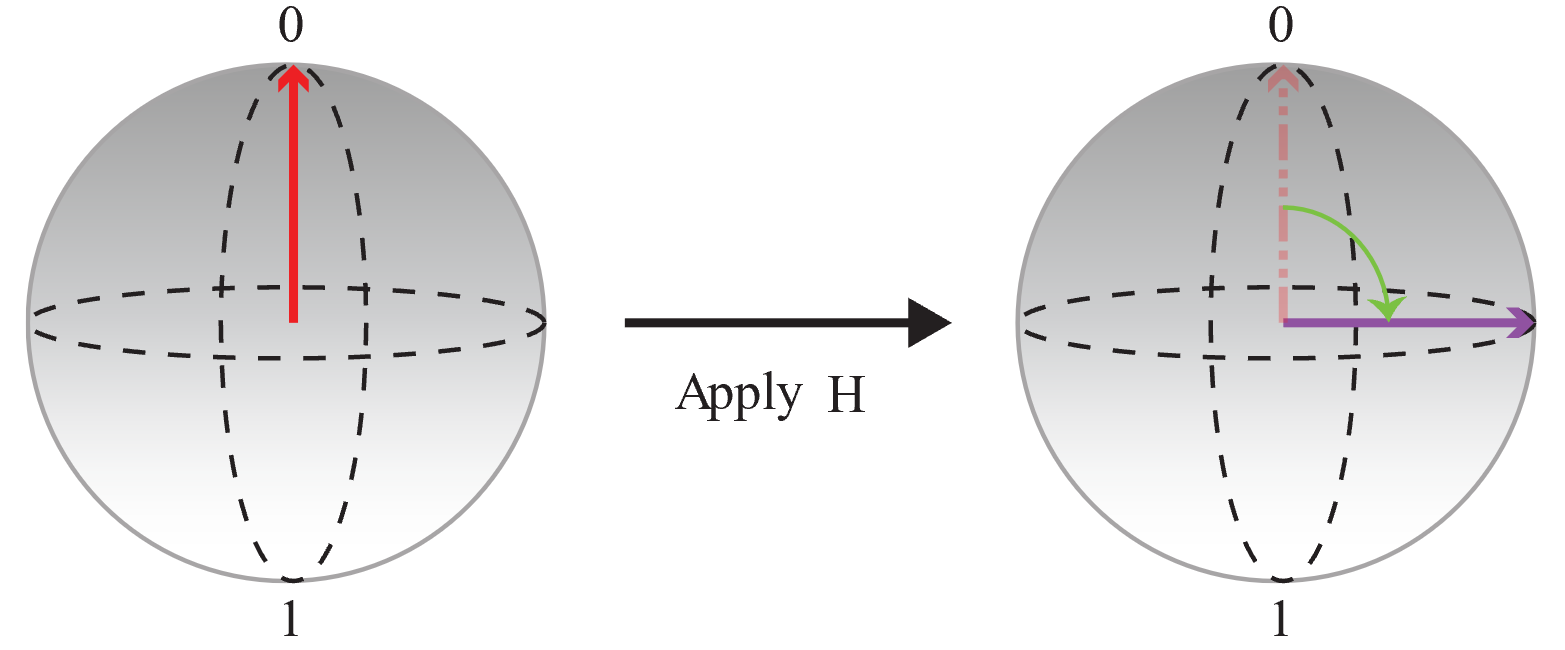
그런 다음, 큐비트를 측정하고 출력을 저장합니다.

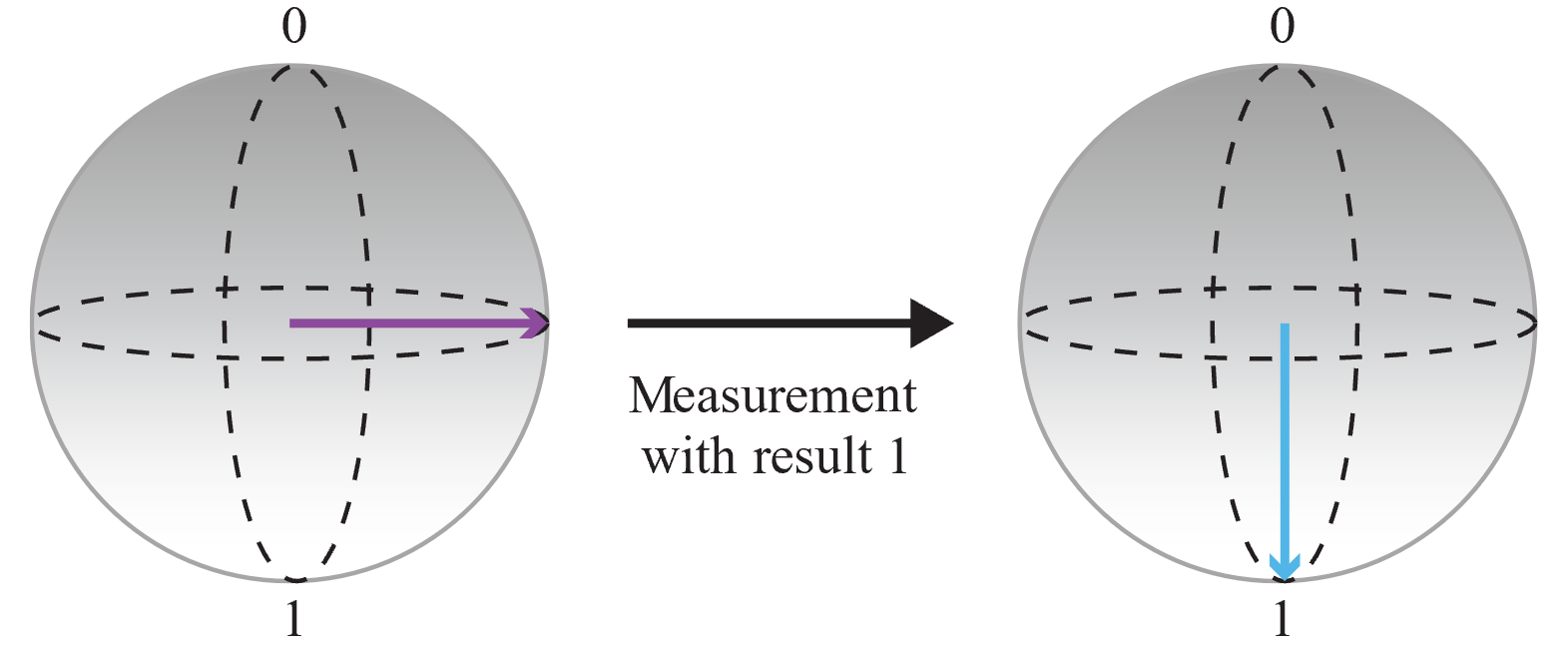
측정 결과는 임의이고 0과 1을 측정할 확률은 동일하므로 완전히 임의 비트를 얻었습니다. 이 연산을 여러 번 호출하여 정수를 만들 수 있습니다. 예를 들어 이 연산을 세 번 호출하여 세 개의 임의 비트를 얻으면 임의의 3비트 숫자(즉, 0~7 사이의 임의 숫자)를 빌드할 수 있습니다.

전체 난수 생성기 작성

먼저 표준 라이브러리에서 Q# 프로그램으로 필요한 네임스페이스를 가져와야 합니다. Q# 컴파일러는 많은 일반적인 함수 및 작업을 자동으로 로드합니다. 그러나 전체 난수 생성기의 경우 두 Q# 네임스페이스의 몇 가지 추가 함수와 연산Microsoft.Quantum.MathMicrosoft.Quantum.Convert이 필요합니다.
```
import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;
```
다음으로 작업을 정의합니다 GenerateRandomNumberInRange . 이 작업은 GenerateRandomBit 작업을 반복적으로 호출하여 비트 문자열을 생성합니다.
```
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
```
잠시 새 코드를 검토해 보겠습니다.
- 최대 max까지의 정수를 표현하는 데 필요한 비트 수를 계산해야 합니다. 네임스페이 BitSizeI 스의 함수는 Microsoft.Quantum.Math 정수를 나타내는 데 필요한 비트 수로 변환합니다.
- SampleRandomNumberInRange 작업은 for 루프를 사용하여 max보다 작거나 같은 값을 생성할 때까지 난수를 생성합니다. for 루프는 다른 프로그래밍 언어의 for 루프와 정확히 동일하게 작동합니다.
- bits 변수는 변경 가능한 변수입니다. 변경 가능한 변수는 계산 중에 변경될 수 있는 변수입니다. set 지시문을 사용하여 변경 가능한 변수의 값을 변경할 수 있습니다.
- 기본 ResultArrayAsInt 네임스페이스의 함수는 Microsoft.Quantum.Convert 비트 문자열을 양의 정수로 변환합니다.
마지막으로 프로그램에 진입점을 추가합니다. 기본적으로 Q# 컴파일러는 작업을 찾고 Main 해당 작업을 처리하기 시작합니다. 작업을 호출 GenerateRandomNumberInRange 하여 0에서 100 사이의 난수를 생성합니다.
```
operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}
```
let 지시문은 계산 도중 변경되지 않는 변수를 선언합니다. 여기서는 최대값을 100으로 정의합니다.

작업에 대한 Main 자세한 내용은 진입점을 참조 하세요.
난수 생성기의 전체 코드는 다음과 같습니다.

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

난수 생성기 프로그램 실행

Azure Quantum의 Copilot 및 Visual Studio Code에서 독립 실행형 Q# 애플리케이션으로 또는 Python 호스트 프로그램을 사용하여 프로그램을 실행할 수 있습니다.

Azure Quantum의 Copilot를 무료로 사용하여 코드를 테스트 Q# 할 수 있습니다. MICROSOFT(MSA) 전자 메일 계정만 있으면 됩니다. Azure Quantum의 Copilot에 대한 자세한 내용은 Azure Quantum 탐색을 참조하세요.

브라우저에서 Azure Quantum 에서 Copilot를 엽니다.

다음 코드를 복사하여 코드 편집기에 붙여넣습니다.

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

실행할 샷 수를 선택하고 실행을 선택합니다.
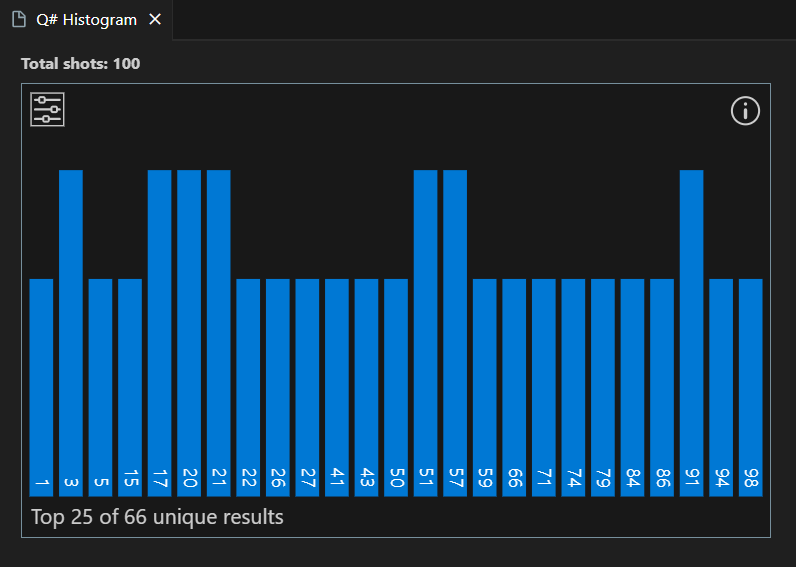
결과는 히스토그램 및 결과 필드에 표시됩니다.
코드 설명을 선택하여 코드를 설명하라는 메시지를 코필로트에게 표시합니다.

팁

Azure Quantum의 Copilot에서 코드 편집기의 오른쪽 모서리에 있는 VS Code 로고 단추를 선택하여 웹용 VS Code에서 프로그램을 열 수 있습니다.

Visual Studio Code를 열고 파일>새 텍스트 파일을 선택하여 새 파일을 만듭니다.
파일을 RandomNumberGenerator.qs로 저장합니다. 이 파일에는 프로그램에 대한 코드가 Q# 포함됩니다.

파일에서 다음 코드를 복사합니다 RandomNumberGenerator.qs .


import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

프로그램을 실행하기 전에 프로필을 무제한target설정 해야 합니다. 보기 - 명령 팔레트를 선택하고Q#
프로그램을 실행하려면 오른쪽 위에 있는 재생 아이콘 드롭다운에서 파일 실행을 선택하고, 앞Q#의 명령 목록에서 실행을 선택하거나, Ctrl+F5를 누릅니 Main() 다. 프로그램은 기본 시뮬레이터에서 작업을 실행 Main() 합니다.
디버그 콘솔에 출력이 표시됩니다.
다른 결과를 보려면 프로그램을 다시 실행합니다.

참고 항목

프로필이 target Unrestricted로 설정되지 않은 경우 프로그램을 실행할 때 오류가 발생합니다.

빈도 히스토그램 그리기

양자 프로그램을 여러 번 실행하여 얻은 결과의 분포를 시각화해 보겠습니다. 빈도 히스토그램은 이러한 결과의 확률 분포를 시각화하는 데 도움이 됩니다.

보기 - 명령 팔레트>다음 파일을 표시Q#"을 입력합니다. 앞의 명령 목록에서 히스토그램을 선택할 수도 있습니다Main(). 히스토그램 창을 열려 Q# 면 이 옵션을 선택합니다.
프로그램을 실행하는 여러 샷 (예: 100개의 샷)을 입력하고 Enter 키를 누릅니 다. 히스토그램이 히스토그램 창에 Q# 표시됩니다.
히스토그램의 각 막대는 가능한 결과에 해당하며, 높이가 결과가 관찰되는 횟수를 나타냅니다. 히스토그램을 실행할 때마다 다른 결과의 수가 다를 수 있습니다.

팁

마우스 스크롤 휠 또는 트랙 패드 제스처를 사용하여 히스토그램을 확대/축소할 수 있습니다. 확대하면 스크롤하는 동안 'Alt'를 눌러 차트를 이동하면 됩니다.
막대를 선택하여 해당 결과의 백분율을 표시합니다.
왼쪽 위 설정 아이콘 을 선택하여 옵션을 표시합니다. 상위 10개 결과, 상위 25개 결과 또는 모든 결과를 표시할 수 있습니다. 결과를 높음에서 낮음 또는 낮음에서 높음으로 정렬할 수도 있습니다.

VS Code에서 명령 팔레트 보기를 > 선택하고 만들기: 새 Jupyter Notebook을 선택합니다.
첫 번째 셀에서 Python 코드에서 패키지를 가져옵니다 qsharp .
```
import qsharp
```

Q# 양자 난수 생성기 프로그램에 대한 코드를 추가합니다. 이렇게 하려면 매직 명령을 사용합니다 %%qsharp . 이 %%qsharp 명령은 Notebook 셀을 형식에서 형식 PythonQ#으로 변경합니다. 이 코드를 두 번째 셀에 복사합니다.

%%qsharp

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

마지막으로 코드를 실행합니다. 동일한 시뮬레이션을 독립적으로 여러 번 실행할 수 있습니다. 각 독립 시뮬레이션을 "샷"이라고 합니다. 예를 들어 시뮬레이션을 100번 실행해 보겠습니다.
```
results = qsharp.run("Main()", shots=100)
print(results)
```

참고 항목

이 코드 조각은 현재 사용 가능한 Azure Quantum 하드웨어targets에서 실행되지 않습니다. 호출 가능한 ResultArrayAsInt 경우 전체 계산 프로필이 있는 QPU가 필요하기 때문에 이 코드 조각은 실행되지 않습니다.

다른 Q# 자습서 살펴보기:

양자 얽 힘은 큐비트를 조작 및 측정하고 중첩 및 얽힘의 효과를 보여 주는 프로그램을 작성하는 Q# 방법을 보여 줍니다.
Grover의 검색 알고리즘 은 Grover의 검색 알고리즘을 Q# 사용하는 프로그램을 작성하는 방법을 보여줍니다.
Quantum Fourier Transforms는 특정 큐비트를 직접 해결하는 프로그램을 작성하는 Q# 방법을 살펴봅니다.
Quantum Katas는 양자 컴퓨팅 및 프로그래밍 요소를 동시에 교육하기 위한 자가 진행 자습서 및 Q# 프로그래밍 연습입니다.

다음을 통해 공유

자습서: Q#에서 양자 난수 생성기 구현

필수 조건

문제 정의

난수 생성기 논리 정의

임의 비트 생성기 작성

블로흐 구를 사용하여 코드 시각화 Q#

전체 난수 생성기 작성

난수 생성기 프로그램 실행

빈도 히스토그램 그리기

피드백

추가 리소스

다음을 통해 공유

자습서: Q#에서 양자 난수 생성기 구현

필수 조건

문제 정의

난수 생성기 논리 정의

임의 비트 생성기 작성

블로흐 구를 사용하여 코드 시각화 Q#

전체 난수 생성기 작성

난수 생성기 프로그램 실행

관련 콘텐츠

피드백

추가 리소스