양자 컴퓨팅에서 T 게이트 및 T 팩터리 역할
이 문서에서는 내결함성 양자 컴퓨팅에서 T 게이트 및 T 팩터리 역할을 설명합니다. 양자 알고리즘을 제공하면 T 게이트 및 T 팩터리를 실행하는 데 필요한 리소스의 예측이 알고리즘의 타당성을 결정하는 데 중요합니다. Azure Quantum Resource Estimator는 알고리즘을 실행하는 데 필요한 T 상태 수, 단일 T 팩터리의 실제 큐비트 수 및 T 팩터리의 런타임을 계산합니다.
양자 게이트의 유니버설 집합
DiVincenzo의 기준에 따르면 확장 가능한 양자 컴퓨터는 범용 양자 게이트 집합을 구현할 수 있어야 합니다. 유니버설 집합에는 양자 계산을 수행하는 데 필요한 모든 게이트가 포함되어 있습니다. 즉, 모든 계산이 유한한 유니버설 게이트 시퀀스로 다시 분해되어야 합니다. 최소한 양자 컴퓨터는 단일 큐비트를 블로흐 구(단일 큐비트 게이트 사용)의 모든 위치로 이동할 수 있을 뿐만 아니라 다중 큐비트 게이트가 필요한 시스템에 얽힘을 도입할 수 있어야 합니다.
클래식 컴퓨터에서 1비트를 1비트로 매핑하는 함수는 4개뿐입니다. 반면, 양자 컴퓨터의 단일 큐비트에는 무한 수의 단위 변환이 있습니다. 따라서 기본 양자 연산 또는 게이트의 유한 집합은 양자 컴퓨팅에서 허용되는 무한 단위 변환 집합을 정확하게 복제할 수 없습니다. 즉, 기존 컴퓨팅과 달리 양자 컴퓨터가 한정된 수의 게이트를 사용하여 가능한 모든 양자 프로그램을 정확하게 구현하는 것은 불가능합니다. 따라서 기존 컴퓨터와 동일한 의미로 양자 컴퓨터를 사용할 수 없습니다. 그 결과, 일련의 게이트가 양자 컴퓨팅에 보편적이라고 말할 때 실제로는 클래식 컴퓨팅에서 의미하는 것보다 약간 약한 것을 의미합니다.
범용성을 위해 양자 컴퓨터는 유한 길이 게이트 시퀀스를 사용하여 유한 오류 내의 모든 단위 행렬만 근사화해야 합니다.
즉, 단위 변환을 이 집합의 게이트 곱으로 작성할 수 있는 경우 게이트 집합은 유니버설 게이트 집합입니다. 규정된 오류 바인딩의 경우 게이트 $집합에서 G_, G_{1}{2}, \ldots, G_N$ 있는 게이트가 있어야 합니다.
$$ G_N G_{N-1}\cdots G_2 G_1 \approx U. $$
행렬 곱하기 규칙은 이 시퀀스의 $첫 번째 게이트 연산인 G_N$ 오른쪽에서 왼쪽으로 곱하는 것이므로 실제로 양자 상태 벡터에 마지막으로 적용됩니다. 보다 공식적으로는, 모든 오류 허용 범위 $\epsilon>0$에 대해 $G_1,\ldots, G_N$이 존재하여 $G_N\ldots G_1$ 및 $U$ 사이의 거리가 최대 $\epsilon$인 경우, 그러한 게이트 집합이 보편성이 있다고 말합니다. 이상적으로 \epsilon의 $이 거리에 도달하는 데 필요한 N$ 값$은 1/\epsilon$을 사용하여 $다 로그적으로 크기를 조정해야$ 합니다.
예를 들어 Hadamard, CNOT 및 T 게이트에 의해 형성된 집합은 모든 양자 계산(큐비트 수)을 생성할 수 있는 범용 집합입니다. Hadamard 및 T 게이트 집합은 단일 큐비트 게이트를 생성합니다.
$$H=\frac{1}{\sqrt{ 1 amp; 1 \\ 1 &-1\end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.&{2}}\begin{bmatrix} $$
양자 컴퓨터에서 양자 게이트는 클리포드 게이트와 비클리포드 게이트( 이 경우 T 게이트)의 두 가지 범주로 분류할 수 있습니다. 클리포드 게이트에서만 만든 양자 프로그램은 클래식 컴퓨터를 사용하여 효율적으로 시뮬레이션할 수 있으므로 양자 이점을 얻으려면 클리포드가 아닌 게이트가 필요합니다. 많은 QEC(양자 오류 수정) 체계에서 이른바 클리포드 게이트는 구현하기 쉽습니다. 즉, 내결함성을 필요로 할 때 클리포드가 아닌 게이트는 매우 비용이 많이 드는 반면, 내결함성을 구현하기 위해 작업 및 큐비트 측면에서 리소스가 거의 필요하지 않습니다. 범용 양자 게이트 집합에서 T 게이트는 일반적으로 클리포드가 아닌 게이트로 사용됩니다.
기본적으로 포함되는 단일 큐비트 클리포드 게이트의 표준 집합은 다음을 Q#포함합니다.
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 &\\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H,$$
$$Y =\begin{bmatrix} 0 & -i \\ amp&; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0-1&\end{bmatrix}= T^4. $$
클리포드가 아닌 게이트(T 게이트)와 함께 이러한 연산은 단일 큐비트에서 모든 단위 변환을 근사화하도록 구성할 수 있습니다.
Azure Quantum 리소스 예측 도구의 T 팩터리
다른 양자 게이트가 범용 양자 계산에 충분하지 않기 때문에 비 클리포드 T 게이트 준비는 매우 중요합니다. 실제 크기 조정 알고리즘에 대해 클리포드가 아닌 작업을 구현하려면 낮은 오류율 T 게이트(또는 T 상태)가 필요합니다. 그러나 논리 큐비트에서 직접 구현하기 어려울 수 있으며 일부 물리적 큐비트에서도 어려울 수 있습니다.
내결함성 양자 컴퓨터에서 필요한 낮은 오류율 T 상태는 T 상태 증류 공장 또는 T 팩터리를 사용하여 짧은 시간 동안 생성됩니다. 이러한 T 공장은 일반적으로 일련의 증류를 포함하며, 각 라운드는 더 작은 거리 코드로 인코딩된 많은 시끄러운 T 상태를 사용하고, 증류 단위를 사용하여 처리하고, 더 큰 거리 코드로 인코딩된 덜 시끄러운 T 상태를 출력하며, 라운드 수, 증류 단위 및 거리 모두 다양할 수 있는 매개 변수가 됩니다. 이 프로시저는 반복됩니다. 여기서 한 라운드의 출력 T 상태는 입력으로 다음 라운드에 공급됩니다.
T 팩터 리의 기간에 따라 Azure Quantum Resource Estimator 는 알고리즘의 총 런타임을 초과하기 전에 T 팩터리를 호출할 수 있는 빈도와 알고리즘 런타임 중에 생성할 수 있는 T 상태 수를 결정합니다. 일반적으로 알고리즘 런타임 동안 단일 T 팩터리의 호출 내에서 생성할 수 있는 것보다 더 많은 T 상태가 필요합니다. 더 많은 T 상태를 생성하기 위해 리소스 추정기는 T 팩터리 복사본을 사용합니다.
T 팩터리 물리적 예측
리소스 추정기는 알고리즘을 실행하는 데 필요한 총 T 상태 수와 단일 T 팩터리 및 해당 런타임에 대한 실제 큐비트 수를 계산합니다.
목표는 가능한 한 적은 T 팩터리 복사본을 사용하여 알고리즘 런타임 내의 모든 T 상태를 생성하는 것입니다. 다음 다이어그램에서는 알고리즘의 런타임 및 하나의 T 팩터리의 런타임 예제를 보여 줍니다. T 팩터리의 런타임이 알고리즘의 런타임보다 짧다는 것을 알 수 있습니다. 이 예제에서는 하나의 T 팩터리에서 하나의 T 상태를 증류할 수 있습니다. 두 가지 질문이 발생합니다.
- 알고리즘이 끝나기 전에 T 팩터리를 얼마나 자주 호출할 수 있나요?
- 알고리즘의 런타임 동안 필요한 T 상태 수를 만드는 데 필요한 T 팩터리 증류 라운드의 복사본 수는 몇 개입니까?
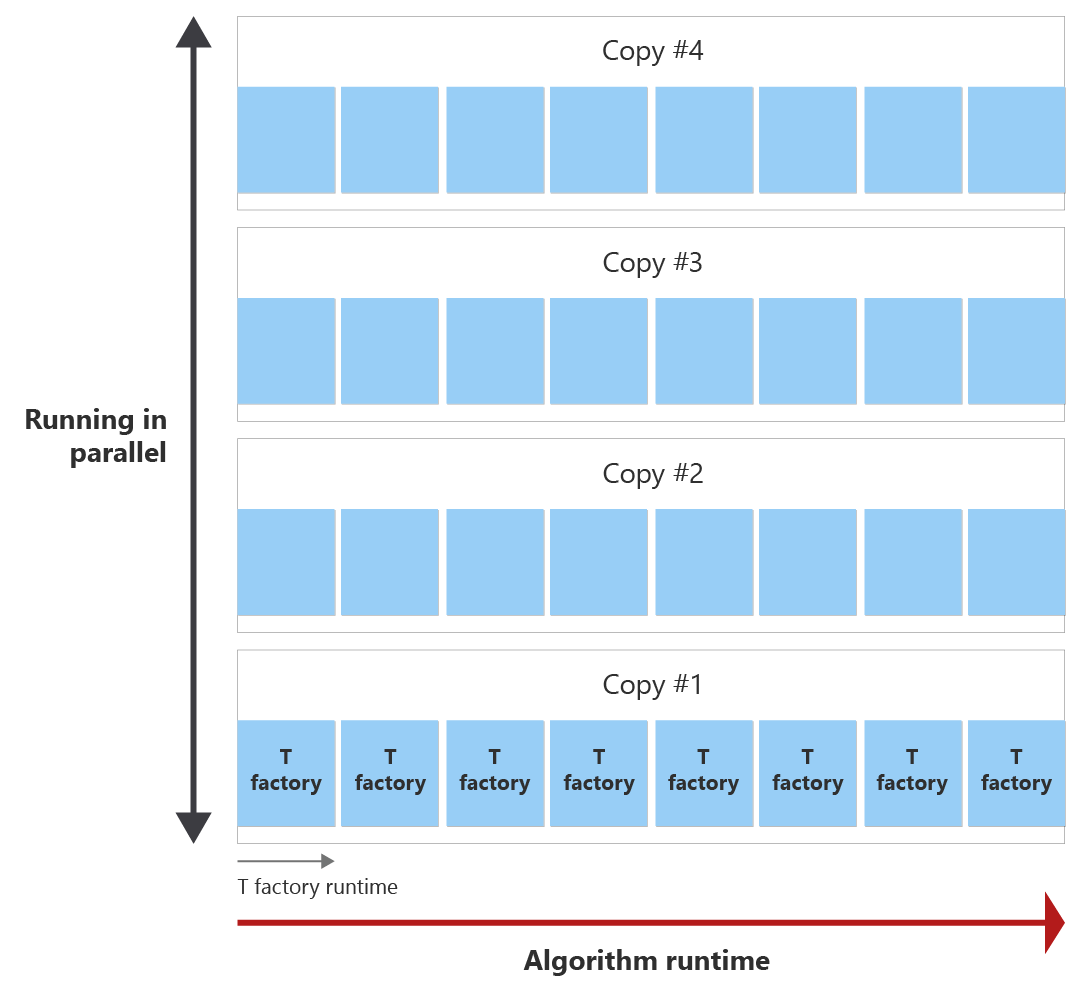
알고리즘이 끝나기 전에 T 팩터리를 8번 호출할 수 있으며, 이를 증류 라운드라고 합니다. 예를 들어 30T 상태가 필요한 경우 단일 T 팩터리는 알고리즘의 런타임 동안 8번 호출되므로 8개의 T 상태를 만듭니다. 그런 다음 필요한 30 T 상태를 증류하기 위해 병렬로 실행되는 T 공장 증류 라운드의 4 개의 사본이 필요합니다.
참고 항목
T 팩터리 복사본 및 T 팩터리 호출은 동일하지 않습니다.
T 상태 증류 공장은 각 라운드가 병렬로 실행되는 증류 단위의 복사본 세트로 구성된 라운드 시퀀스로 구현됩니다. Resource Estimator는 하나의 T 팩터리를 실행하는 데 필요한 실제 큐비트 수와 T 팩터리 실행 기간(기타 필수 매개 변수 중)을 계산합니다.
T 팩터리의 전체 호출만 수행할 수 있습니다. 따라서 모든 T 팩터리 호출의 누적된 런타임이 알고리즘 런타임보다 작은 경우가 있을 수 있습니다. 큐비트는 서로 다른 라운드에서 재사용되므로 하나의 T 팩터리에 대한 실제 큐비트 수는 한 라운드에 사용되는 최대 물리적 큐비트 수입니다. T 팩터리의 런타임은 모든 라운드에서 런타임의 합계입니다.
참고 항목
물리적 T 게이트 오류 비율이 필요한 논리적 T 상태 오류 비율보다 낮으면 리소스 예측 도구에서 적절한 리소스 추정을 수행할 수 없습니다. 리소스 예측 작업을 제출할 때 필요한 논리적 T 상태 오류 비율이 너무 낮거나 너무 높기 때문에 T 팩터리를 찾을 수 없는 경우가 발생할 수 있습니다.
자세한 내용은 실질적인 양자 이점으로 확장하기 위한 평가 요구 사항의 부록 C를 참조하세요.