c# Multitasking Case Study – Evolutionary Hill Climber for the Traveling Salesman Problem
In this article we show how to make a better simple evolutionary hill climber for the Traveling Salesman problem using the concurrent task creation and manipulation facilities of the C# .NET Framework 4.5.2. Multitasking is one of the two methods of parallel processing offered by C# .NET framework 4.5.2 the other is a parallel loop.
The Traveling Salesman Problem (TSP) is a well-known combinatorial optimization problem. The classical TSP consists of finding the minimal round-trip tour of n cities where the distance is the Euclidean distance between cities. This problem is known to be NP-hard so there is no available deterministic polynomial time algorithm to solve the problem. There are many techniques that have been utilized to find optimal or near optimal solutions to the standard TSP. Among the first computerized methods tried on the TSP was simulated annealing (SA). This algorithm uses an analogy to the annealing process in metallurgy. Alloys are heated to a very high temperature then allowed to slowly cool and sometimes this procedure creates a stronger or more malleable metal. SA uses a high initial simulated temperature and a cooling schedule. In a minimization problem such as the TSP when an uphill move is calculated then sometimes we allow the move with a certain probability via the Metropolis formula. In all our implementations of SA for the classical TSP we use the swap operator to generate new moves. Another early technique used for computer solutions of the TSP were genetic algorithms (GAs) with or without crossover operators. GAs were the earliest computer modeling of simulated biological evolution. In a GA for the TSP the chromosome consists of a tour of the cities and each gene is city. The simplest mutation operator is the reciprocal swap operator just like the one used in SA. There a number of crossover operators developed for the TSP including path crossover. Other evolutionary methods tried on the TSP are the ant colony optimization (ACO) and the particle swarm optimization (PSO), the first of course, uses a simulated pheromone trail to find the optimal solution, and the latter models an insect or bird swarm finding a geographic location. Both the ACO and PSO are social evolutionary techniques. Two of the most successful TSP solvers are the Lin-Kernigan heuristic and linear programming.
Evolutionary hill climbers are strongly related to GAs with the major difference being the sole use of mutation as the only evolutionary operator. Hill climbers follow a gradient either in ascent or descent depending whether maximization or minimization is involved. If the search space has many local optima the hill climber can get stuck in a local optima and never find the global optimum or optima. One way to avoid getting stuck in a local minimum or maximum is to use a population of hill climbers.
Before going any further, we need elucidate the characteristics of the test-bed computer and its architecture. The computer in question is a relatively new (late October 2015) Dell XPS 8900 with an Intel i7-6700K CPU rated at a clock frequency of 4.00 GHz with 16 GB DDR4 RAM and a 2 TB hard-drive with a 32 GB SSD buffer (a hybrid hard-drive). The CPU has 4 cores and 8 logical processors. The operating system is Windows 10 Pro and the C# integrated development environment (IDE) is Visual Studio 2015 Community. The .NET Framework 4.5.2 is utilized.
Now with the computer architecture illuminated, we can delve into the details of the simple evolutionary hill climber (EHC) algorithm. To be succinct the EHC uses a population of chromosomes with a two tournament selection of an individual chromosome to be mutated by the reciprocal swap operator each and every generation. The replacement scheme is elitist meaning that the newly created child chromosome replaces the worst individual in the current population. The fitness function is the tour length of the chromosome (simply an initial random tour). We embody this algorithm in a task with the following state structure:
public struct State
{
public double[] x, y;
public int generations, number, population, seed;
public List<int> minTour;
public State(
double[] x, double[] y,
int generations, int number, int population, int seed)
{
this.x = x;
this.y = y;
this.generations = generations;
this.number = number;
this.population = population;
this.seed = seed;
minTour = new List<int>();
}
}
We now display the actual code of the task:
001.private void EHCTask(object o)
002.{
003. State s = (State)o;
004. double minDistance = double.MaxValue;
005. double[] distance = new double[s.population];
006. int[,] chromosome = new int[s.population, s.number];
007. Random random = new Random(s.seed);
008.
009. for (int p = 0; p < s.population; p++)
010. {
011. bool[] used = new bool[s.number];
012. int[] city = new int[s.number];
013.
014. for (int n = 0; n < s.number; n++)
015. used[n] = false;
016.
017. for (int n = 0; n < s.number; n++)
018. {
019. int i;
020.
021. do
022. {
023. i = random.Next(s.number);
024. }
025. while (used[i]);
026.
027. used[i] = true;
028. city[n] = i;
029. }
030.
031. for (int n = 0; n < s.number; n++)
032. chromosome[p, n] = city[n];
033.
034. distance[p] = TourDistance(s.x, s.y, s.number, city);
035.
036. if (distance[p] < minDistance)
037. {
038. minDistance = distance[p];
039.
040. if (s.minTour.Count == s.number)
041. for (int n = 0; n < s.number; n++)
042. s.minTour[n] = chromosome[p, n];
043.
044. else
045. for (int n = 0; n < s.number; n++)
046. s.minTour.Add(chromosome[p, n]);
047. }
048. }
049.
050. for (int g = 1; g <= s.generations; g++)
051. {
052. double childDistance;
053. int i, j, p;
054. int[] child = new int[s.number];
055.
056. i = random.Next(s.population);
057. j = random.Next(s.population);
058.
059. if (distance[i] < distance[j])
060. p = i;
061.
062. else
063. p = j;
064.
065. for (int n = 0; n < s.number; n++)
066. child[n] = chromosome[p, n];
067.
068. do
069. {
070. i = random.Next(s.number);
071. j = random.Next(s.number);
072. }
073. while (i == j);
074.
075. int t = child[i];
076.
077. child[i] = child[j];
078. child[j] = t;
079. childDistance = TourDistance(s.x, s. y, s.number, child);
080.
081. int maxIndex = int.MaxValue;
082. double maxD = double.MinValue;
083.
084. for (int q = 0; q < s.population; q++)
085. {
086. if (distance[q] >= maxD)
087. {
088. maxIndex = q;
089. maxD = distance[q];
090. }
091. }
092.
093. int[] index = new int[s.population];
094. int count = 0;
095.
096. for (int q = 0; q < s.population; q++)
097. {
098. if (distance[q] == maxD)
099. {
100. index[count++] = q;
101. }
102. }
103.
104. maxIndex = index[random.Next(count)];
105.
106. if (childDistance < distance[maxIndex])
107. {
108. distance[maxIndex] = childDistance;
109.
110. for (int n = 0; n < s.number; n++)
111. chromosome[maxIndex, n] = child[n];
112.
113. if (childDistance < minDistance)
114. {
115. minDistance = childDistance;
116.
117. for (int n = 0; n < s.number; n++)
118. s.minTour[n] = child[n];
119. }
120. }
121. }
122.}
Lines 9-48 initialize the population to random tours. Lines 56-63 are the 2-tournament selection code. The lines 58-78 perform the reciprocal swap and finally lines 81-121 are the elitist replacement scheme.
We use an array of Task objects. The length of the array is dictated by the computer architecture and probably optimally the number of physical processors in our case 4. We create and start 4 tasks and then wait until all the tasks are completed. We now hopefully have 4 near optimal tours. At this point we run another partial EHC with the 4 found tours and attempt to refine them to an optimal tour.
State[] states = new State[cores];
Task[] tasks = new Task[cores];
for (int i = 0; i < cores; i++)
{
states[i] = new State(x, y, generations, number, population, seed + i);
tasks[i] = new Task(EHCTask, states[i]);
tasks[i].Start();
}
Task.WaitAll(tasks);
// now run another hill climber on the best tours found thus far
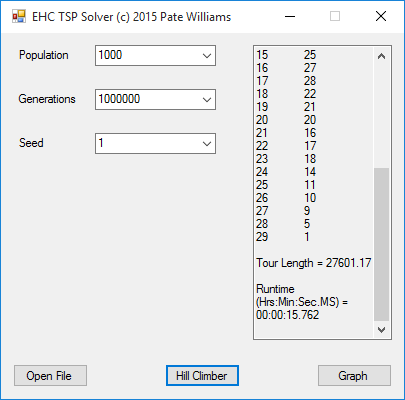
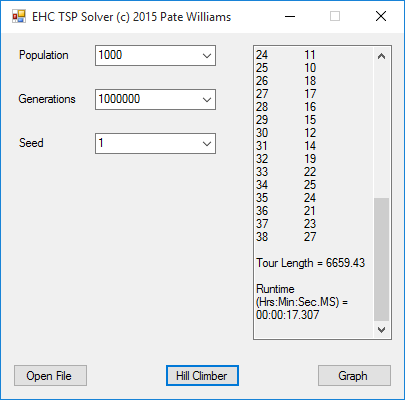
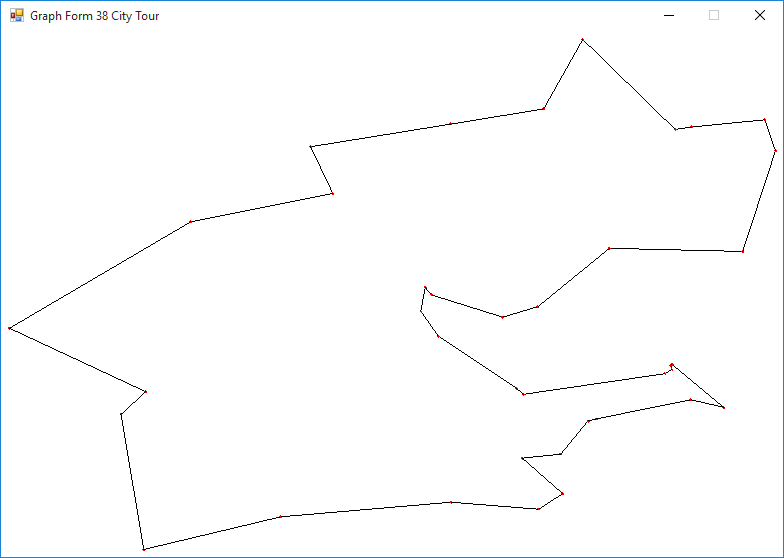
Now we move on to the crux of the article namely the results on real world TSP instances. You can find a number of test examples at the website: http://www.math.uwaterloo.ca/tsp/world/. The first test of our multitasking EHC is the 29 city tour of Western Sahara with stated optimum of 27603 at the preceding website. Using a population of 1000 and 1000000 generations we get a tour of length 27601.17 in 15.762 seconds of computation. In a previous effort using an SA program we got the same result in 00:01:12.366 (Hrs-Min-Sec.MS) on another much older computer. Moving along to the next example we are still in Africa with a 38 city tour of Djibouti. The stated optimum is 6656. Using the same parameters, we get 6659.43 in 17.307 seconds. Our SA application gets 6659.91 in 9.410 seconds om an older Core i7 system. The original single task EHC finds the same local minimum 6659.43 in 17.206 seconds on an old computer. The results for the 194 city tour of Qatar are not worth reporting. So it seems this extremely simple algorithm is probably limited to tours of approximately 50 cities or less and perhaps even 40 cities or less.