色の回転

4 次元の色空間での回転は、視覚化するのが困難です。 色要素の 1 つを固定することに同意すれば、回転の視覚化を容易にすることができます。 たとえば、アルファ要素を 1 (完全に不透明) に固定することに同意したとします。 そうすると、次の図に示すように、赤、緑、青を軸とする 3 次元の色空間を視覚化できます。

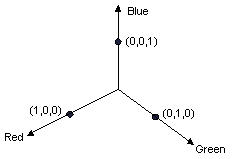
色は、3-D 空間の点と考えることができます。 たとえば、空間内の点 (1, 0, 0) は赤を表し、空間内の点 (0, 1, 0) は緑を表します。

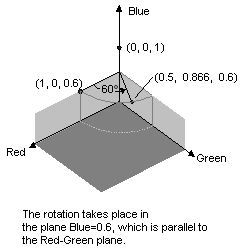
次の図は、赤と緑の平面で 60 度の角度を使用して、色 (1, 0, 0) を回転させるということがどのようなことなのかを示したものです。 赤と緑の平面と平行である平面内での回転は、青の軸を中心とした回転であると考えることができます。

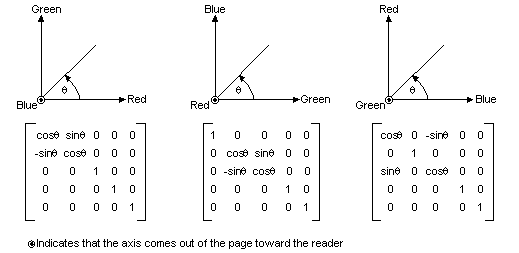
次の図は、3 つの座標軸 (赤、緑、青) のそれぞれの回転を実行するカラー マトリックスを初期化する方法を示しています。

次の例では、1 つの色 (1, 0, 0.6) だけで塗られた画像を使用し、青の軸を中心として 60 度の回転を適用しています。 回転の角度は、Red-Green平面と平行な平面でスイープされます。

Image            image(L"RotationInput.bmp");
ImageAttributes  imageAttributes;
UINT             width = image.GetWidth();
UINT             height = image.GetHeight();
REAL             degrees = 60;
REAL             pi = acos(-1);  // the angle whose cosine is -1.
REAL             r = degrees * pi / 180;  // degrees to radians

ColorMatrix colorMatrix = {
   cos(r),  sin(r), 0.0f, 0.0f, 0.0f,
   -sin(r), cos(r), 0.0f, 0.0f, 0.0f,
   0.0f,    0.0f,   1.0f, 0.0f, 0.0f,
   0.0f,    0.0f,   0.0f, 1.0f, 0.0f,
   0.0f,    0.0f,   0.0f, 0.0f, 1.0f};
   
imageAttributes.SetColorMatrix(
   &colorMatrix, 
   ColorMatrixFlagsDefault,
   ColorAdjustTypeBitmap);
   
graphics.DrawImage(&image, 10, 10, width, height);

graphics.DrawImage(
   &image, 
   Rect(130, 10, width, height),  // destination rectangle 
   0, 0,        // upper-left corner of source rectangle 
   width,       // width of source rectangle
   height,      // height of source rectangle
   UnitPixel,
   &imageAttributes);

次の図は、左側の元の画像と、右に色が回転した画像を示しています。

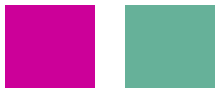
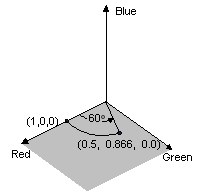
前のコード例で実行した色の回転は、次のように視覚化できます。