回転

多くの CAD アプリケーションは、クライアント領域に描画されたオブジェクトを回転させる機能を提供します。 回転機能を含むアプリケーションでは 、SetWorldTransform 関数を使用して、適切なワールド空間をページ空間変換に設定します。 この関数は、適切な値を含む XFORM 構造体へのポインターを受け取ります。 XFORM の eM11、eM12、eM21、および eM22 メンバーは、回転角度のコサイン、サイン、負のサイン、コサインをそれぞれ指定します。

回転が発生すると、オブジェクトを構成する点は座標空間の原点に対して回転されます。 次の図は、ワールド座標空間からページ座標空間にコピーしたときに 30 度回転した 20 x 20 単位の四角形を示しています。

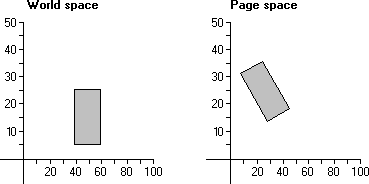
前の図では、四角形の各点が座標空間の原点に対して 30 度回転しました。

次のアルゴリズムは、座標空間の原点に対して角度 A で回転される点 (x,y) の新しい x 座標 (x ') を計算します。

x' = (x * cos A) - (y * sin A) 

次のアルゴリズムは、原点に対して角度 A で回転される点 (x,y) の y 座標 (y ') を計算します。

y' = (x * sin A) + (y * cos A) 

2 つの回転変換は、次のように 2 by 2 行列で組み合わせることができます。

|x' y'| == |x y| * | cos A   sin A| 
                   |-sin A   cos A| 

回転を生成した 2 対 2 の行列には、次の値が含まれています。

| .8660    .5000| 
|-.5000    .8660| 

回転アルゴリズムの派生

回転アルゴリズムは、2 つの角度の和 (A1 と A2) の三角関数を 2 つの角度の三角関数の観点から表すことができることを示す三角関数の加算定理に基づいています。

sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2) 
cos(A1 + A2) = (cos A1 * cos A2) - (sin A1 * sin A2) 

次の図は、新しい位置 p' に反時計回りに回転した点 p を示しています。 さらに、座標空間の原点から各ポイントに描画された線と、各ポイントから x 軸を通って描画された線によって形成される 2 つの三角形が表示されます。

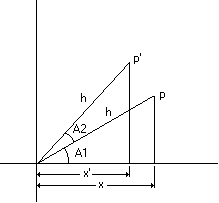
三角法を用いて、点pのx座標は、低辺辺hの長さをA1のコサインで乗算することによって得ることができる。

x = h * cos A1 

点pのy座標は、次辺辺hの長さをA1のサインで乗算することによって得ることができる。

y = h * sin A1 

同様に、点 p' の x 座標は、次辺辺 h の長さと のコサイン (A1 +A2) を乗算することによって取得できます。

x' = h * cos (A1 + A2) 

最後に、点 p' の y 座標は、次辺辺 h の長さに ( A1 + A2 ) のサインを乗算することによって取得できます。

y' = h * sin (A1 + A2) 

加算定理を使用すると、上記のアルゴリズムは次のようになります。

x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2) 
y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2) 

角度 A2 で回転した特定の点の回転アルゴリズムは、 (h * cos A1) の発生ごとに x を置き換え、 (h * sin A1) の発生ごとに y を置き換えることによって取得できます。

x' = (x * cos A2) - (y * sin A2) 
y' = (x * sin A2) + (y * cos A2)