パラメータカーブ
メディア パラメータは、時間の経過と同時に曲線に従うことが可能です。 各曲線は、数式と 2 つの終点によって記述されます。 各終点は、参照時間とその時点の曲線の値によって定義されます。 この数式は、点間の中間値を計算するために使用され、曲線の形状を決定します。 考えられる曲線は次のとおりです。
- ジャンプ
- Linear
- Square
- 逆二乗
- サイン
"ジャンプ" とは、終了値に直接ジャンプすることを意味します。 その他の曲線を次の図に示します。
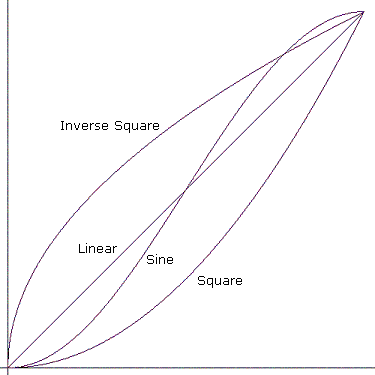
数学的には、曲線は次のように機能します。 曲線が v₀ の値を持つ時刻 t₀ で始まり、 時刻t₁ で v₁ の値で終わるとします。 曲線を定義する 2 つの点は (t₀, v₀) と (t₁, v₁) です。
- Δt を曲線の合計期間 t₁–t₀ とします。
- Δv を開始値と終了値 v₁–v₀ の間隔にします。
- t₀ = t= t<₁<のような t はいつでも、Δt' = t–t₀ を許可します。
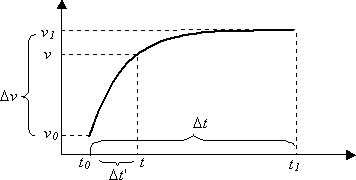
時刻 t のパラメーターの値は次のとおりです。
v = f(Δt' /Δt ) *Δvv + ₀
ここで、f(x) は曲線の種類によって決定される関数です。
- 線形: y = x
- 正方形: y = x^2
- 逆二乗: y = sqrt(x)
- 正弦: y = [ sin(πx – π/2) + 1 ] / 2
Δt'Δtが < 0から1の範囲であることを観察してください。 したがって、f(x) の範囲も 0 から 1 で、 v は常に v₀ と v₁ の間にあります。 これは、v₀ v₁ < またはその逆に関係なく当てはまります。 つまり、曲線は四角形 (t₀、 v₀、 t₁、 v₁) で囲まれます。
サイン曲線の場合、(πx – π/2) の値は -π/2 から π/2 の範囲です。つまり、sin(πx – π/2) の範囲は –1 から 1 です。 その後、f(x) が範囲 (0 ~ 1) に収まるよう、結果が正規化されます。
関連トピック