ベクトル、頂点、および四元数
Direct3D では、頂点は位置と方向を表します。 プリミティブの各頂点は、位置を決定するベクトル、色、テクスチャ座標、および方向を決定する法線ベクトルによって示されます。
四元数は、3 要素のベクトルを定義する [x, y, z] の値に 4 つ目の要素を追加します。 四元数は、3D 回転で一般的に使われている、行列による方法の代わりとなるものです。 四元数では、3D 空間内の軸と、その軸を中心とする回転が表されます。 たとえば、1 つの四元数で、軸 (1,1,2) と 1 ラジアンの回転を表すことができます。 四元数は有用な情報を伝達しますが、その真価が発揮されるのは、四元数に対して合成と補間という 2 つの操作を実行する場合です。
四元数に対する合成の実行は、四元数を結合する操作と似ています。 2 つの四元数の合成は次のように表記されます。
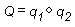
ジオメトリに適用される 2 つの四次元数の合成は、"軸₂ を中心に回転₂ でジオメトリを回転させ、次に軸₁ を中心に回転₁ で回転させる" ことを意味します。この場合、Q は、ジオメトリに q₂、q₁ の順に適用した結果の単一の軸を中心とした回転を表します。
四元数の補間を使うと、1 つの軸と方向から別の軸と方向への滑らかで適切なパスをアプリケーションで計算できます。 したがって、q₁ と q₂ の間を補完すれば、1 つの方向から別の方向へのアニメーションを簡単に実現できます。
合成と補間を同時に使うと、複雑に見えるジオメトリの操作を簡単な方法で実行できます。 たとえば、ジオメトリを特定の方向に回転させる場合を考えます。 axis₂ を中心に r₂ 度回転させた後、axis₁ を中心に r₁ 度回転させようとしていますが、最終的な四元数はわかっていません。 合成を使えば、ジオメトリに対する 2 つの回転を結合して、結果を表す単一の四元数を得ることができます。 さらに、元の四元数から合成後の四元数までを補間すると、あるジオメトリから別のジオメトリへの滑らかな遷移を実現できます。
関連トピック