回帰とは何でしょうか?
回帰は、単純で一般的で、非常に有用なデータ分析手法であり、多くの場合、口語的に "線の適合" と呼ばれます。最も単純な形式では、回帰は 1 つの変数 (特徴) と別の変数 (ラベル) の間の直線に適合します。 より複雑な形式の回帰では、1 つのラベルと複数の特徴の間で非線形の関係を見つけることができます。
線形単回帰
単純線形回帰では、単一の特徴と通常は連続するラベルの間の線形関係がモデル化され、特徴によってラベルを予測することができます。 視覚的には次のように表されます。

単純線形回帰には、2 つのパラメーターがあります。切片 (c) は、特徴がゼロに設定されたときのラベルの値を示します。傾き (m) は、特徴が 1 ポイント増加ごとにラベルがどの程度増加するかを示します。
数学的に考える場合は、単に次のようになります。
y = mx + c
y はラベルで、x は特徴です。
たとえば、このシナリオでは、年齢に基づいて病犬の体温上昇を予測しようとした場合、モデルは次のようになります。
体温 = m * 年齢 + c
適合手順の間に、"m" と "c" の値を求める必要があります。 m = 0.5 および c = 37 とわかった場合、図は次のようになります。
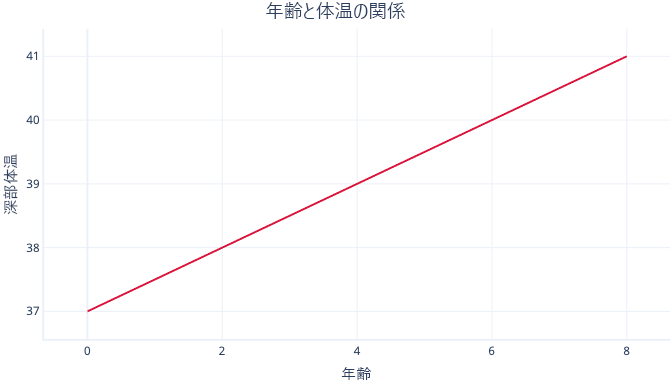
これは、37°C から始まって年齢が 1 歳増すごとに体温が 0.5°C 上昇することを意味します。
線形回帰の適合
通常は、既存のライブラリを使用して、回帰モデルを自動的に適合します。 通常、回帰の目的は、発生する誤差の量が最も少ない線を見つけることです。ここでの誤差は、実際のデータ ポイント値と予測値の差を意味します。 たとえば、次の図で、黒い線は、予測 (赤い線) と 1 つ の実際の値 (ドット) の間の誤差を示しています。
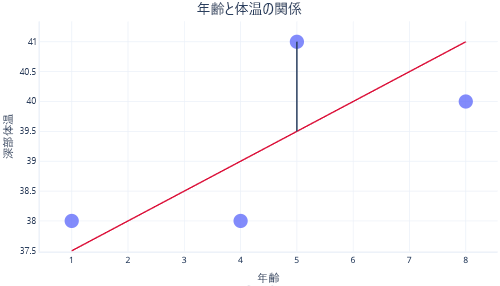
y 軸上でこれら 2 つの点を見ると、予測が 39.5 であったのに対し、実際の値は 41 であったことがわかります。
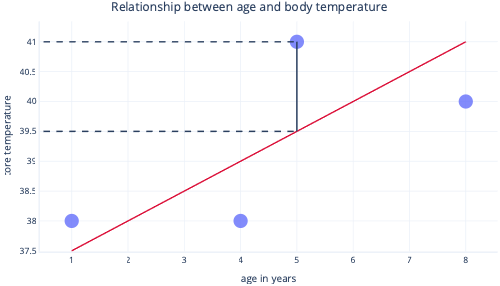
したがって、このデータポイントではモデルは 1.5 だけ間違っていました。
通常は、残差平方和を最小にすることでモデルを適合させます。 これは、コスト関数が次のように計算されることを意味します。
- 各データ ポイントで実際の値と予測値の差を計算します (上記のように)。
- これらの値を二乗します。
- これらの二乗値の合計 (または平均) を求めます。
この二乗ステップは、すべてのポイントが線に均等に寄与するわけではないことを意味します。外れ値 (予想されるパターンに収まらない点) は過度に大きい誤差になり、行の位置に影響を与える可能性があります。
回帰の長所
回帰手法には、より複雑なモデルにはない多くの長所があります。
予測可能で簡単に解釈できる
回帰は、単純な数学的方程式を表し、グラフ化できる場合が多いため、簡単に解釈できます。 より複雑なモデルは、予測を行う方法や、特定の入力でどのように動作するかを理解するのが難しいため、"ブラック ボックス" ソリューションと呼ばれることがよくあります。
推定が容易である
回帰では、データセットの範囲外の値を予測する推定を簡単に行うことができます。 たとえば、前の例では、9 歳の犬では体温が 40.5°C になると、簡単に推定できます。 推定には常に注意が必要です。このモデルでは、90 歳になると、水が沸騰するくらいの体温になると予測されます。
通常、最適な適合が保証される
ほとんどの機械学習モデルでモデルの適合に使用される勾配降下では、勾配降下アルゴリズムのチューニングが伴い、最適な解が見つかる保証はありません。 一方、コスト関数として平方和を使用する線形回帰では、反復的な勾配降下手順は実際には必要ありません。 代わりに、巧妙な数学的処理を使用して、線を配置する最適な場所を計算できます。 その数学的処理はこのモジュールの範囲外ですが、線形回帰では、(サンプル サイズが大きすぎない限り) 適合プロセスに特別な注意を払う必要はなく、最適なソリューションが保証されることを知っておくのは役に立ちます。