回帰とは何でしょうか?
回帰は、観察される対象の特性を表すデータの変数 ("特徴" と呼ばれます) と、予測しようとしている変数 ("ラベル" と呼ばれます) の間にリレーションシップを確立することによって機能します。
先ほどの会社では、自転車をレンタルし、特定の日に予想されるレンタル数を予測したいと考えていました。 この場合、特徴には曜日、月などが含まれ、ラベルは自転車のレンタル数です。
モデルをトレーニングするには、特徴量とラベルの既知の値を含むデータ サンプルから始めます。この例では、日付、気象条件、自転車のレンタル数を含む履歴データが必要です。
次に、このデータ サンプルを以下の 2 つのサブセットに分割します。
- 特徴量の値と既知のラベル値の間の関係をカプセル化する関数を決定するアルゴリズムを適用する "トレーニング" データセット。
- モデルを評価するために使用できる "検証" または "テスト" データセット。このデータセットを使用してラベルの予測を生成し、それらを実際の既知のラベル値と比較します。
既知のラベル値を持つ履歴データを使用してモデルをトレーニングする回帰は、"教師あり" 機械学習の例です。
簡単な例
ここでは、トレーニングと評価のプロセスがどのように機能するかを簡単に説明します。 たとえば、特徴の 1 つである 1 日の平均気温を使用して自転車のレンタル数のラベルを予測するようにシナリオを簡略化したとします。
最初の例では、1 日の平均気温の特徴量と自転車レンタル数のラベルの既知の値を含むいくつかのデータから始めます。
| 気温 | レンタル数 |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
では、観測値の 5 つを "ランダムに" 選択し、それを使って回帰モデルをトレーニングしましょう。 "モデルのトレーニング" について話している場合、温度特徴 (x と呼ぶ) を使用してレンタルの数 (y と呼ぶ) を計算できる関数 (数式 f と呼ぶ) を見つけることを意味します。 言い換えると、f(x) = y という関数を定義する必要があります。
トレーニング データセットは次のようになります。
| x | y |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
まず、グラフに x と y のトレーニング値をプロットします。
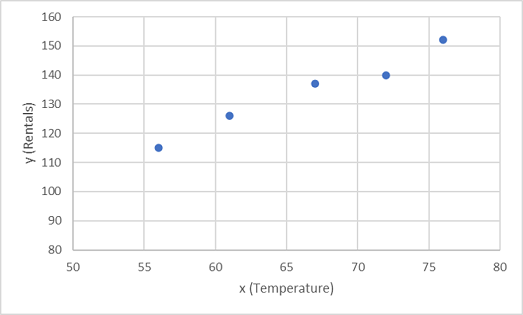
ここで、ランダムな変動を許しながらこれらの値を関数に適合させる必要があります。 プロットされた点がほぼまっすぐな対角線を成していることがわかります。つまり、x と y の間には明確な "線形" 関係があるため、データ サンプルに対して最も近い線形関数を見つける必要があります。 この関数を決定するために使用できるさまざまなアルゴリズムがあります。最終的には、次のようにプロットされた点からの全体的な差異が最小限となる直線を見つけます。
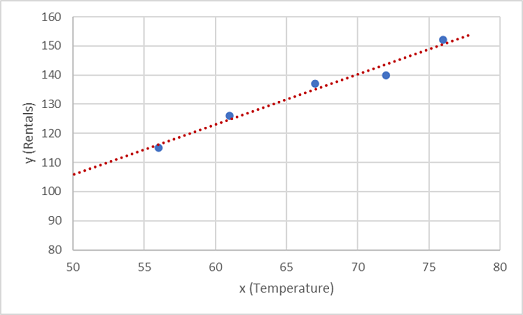
この直線は、x の任意の値に直線の "傾き" およびその "切片" (x が 0 のときに直線が y 軸と交わる点) を適用して y を計算する線形関数を表します。 この例では、直線を左に延長すると、x が 0 のときに y は約 20 であることがわかります。また、直線の傾きについては、x に沿って 1 単位だけ右に移動したときに、y は約 1.7 増加します。 したがって、ここでの f 関数は 20 + 1.7x と計算できます。
ここまでで予測関数を定義しました。これを使用して保持していた検証データのラベルを予測し、予測された値 (通常は、記号 ŷ または "y ハット" で表します) と実際の既知の y 値を比較します。
| x | y | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
プロットで y と ŷ の値を比較してみましょう。
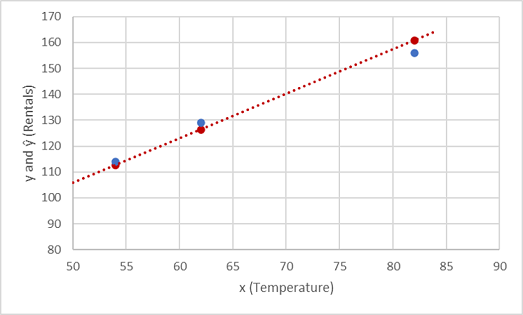
関数の直線上にプロットされた点は、関数によって計算された ŷ の予測値であり、プロットされたもう一方の点は実際の y の値です。
予測値と実際の値の間の分散を測定するにはさまざまな方法があります。これらのメトリックを使用すると、モデルの予測精度を評価できます。
Note
機械学習は統計学と数学に基づいているため、統計学者と数学者 (したがって、データ サイエンティスト) が使用する特定の用語に注意することが重要です。 "予測された" ラベル値と "実際の" ラベル値の差は、"誤差" の尺度と考えることができます。 ただし、現実には、"実際の" 値はサンプルの観測値に基づいています (これ自体がランダムな分散を持つ場合があります)。 "予測された" 値 (ŷ) と "観測された" 値 (y) を比較していることを明確にするために、それらの差を "残差" と呼びます。 すべての検証データ予測の残差を集計し、予測パフォーマンスの尺度としてモデルの全体的な "損失" を計算することができます。
損失を測定する最も一般的な方法の 1 つは、個々の残差を 2 乗して合計し、平均を計算することです。 残差を 2 乗することは、"絶対" 値に基づいて計算を行い (差が正か負かは無視されます)、より大きな差に対する重みを増やすことを意味します。 このメトリックは、"平均二乗誤差" と呼ばれています。
この例の検証データの場合、計算は次のようになります。
| ○ | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2.2 | 4.84 |
| 129 | 125.4 | 3.6 | 12.96 |
| SUM | ∑ | 29.36 | |
| 平均 | x̄ | 9.79 |
このように、MSE メトリックに基づくモデルの損失は 9.79 です。
それでは、これはどれだけ優れているのでしょうか。 MSE の値は意味のある測定単位では表されていないため、判断するのは困難です。 値が小さいほどモデルの損失は少なく、予測がより優れていることはわかります。 そのため、これは 2 つのモデルを比較して最適なモデルを見つけるのに便利なメトリックです。
場合によっては、予測されるラベル値自体と同じ測定単位 (この例ではレンタルの数) で損失を表す方が便利です。 これは、MSE の平方根を計算することで可能になり、当然ですが、"二乗平均平方根誤差" (RMSE) と呼ばれるメトリックが生成されます。
√9.79 = 3.13
このモデルの RMSE は、損失が 3 をわずかに超えていることを示しています。これは大まかにいえば、正しくない予測は平均してレンタル数で約 3 誤っていることを意味すると解釈できます。
回帰の損失を測定するために使用できるメトリックは他にも多数あります。 たとえば、R2 (R の 2 乗) ("決定係数" とも呼ばれます) は、x と y の 2 乗の間の相関関係です。 これにより、モデルで説明できる分散の量を測定する 0 ~ 1 の値が生成されます。 一般に、この値が 1 に近いほど、モデルの予測精度が向上します。