演習 : モデルの出力を視覚化する

8 分

このユニットでは、操作してきたノートブックに Matplotlib をインポートし、インラインの Matplotlib 出力をサポートするようにノートブックを構成します。

前のセクションで作成した Azure ノートブックに戻ります。ノートブックを閉じた場合は、Microsoft Azure Notebooks ポータルにもう一度サインインし、ノートブックを開き、[セル] ->[すべて実行] を使用して、開いたノートブック内のすべてのセルを再実行します。
ノートブックの末尾にある新しいセルで、次のステートメントを実行します。フォントキャッシュに関連する、表示された警告メッセージは無視します。
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns

sns.set()
```
最初のステートメントは、ノートブックを作成したときに選んだ Python カーネルによってサポートされるいくつかの magic コマンドの 1 つです。これにより、Jupyter では、show を繰り返し呼び出すことなく、ノートブックに Matplotlib 出力をレンダリングできます。これは、Matplotlib 自体への参照の前に示される必要があります。最後のステートメントでは、Matplotlib からの出力を拡張するように Seaborn を構成します。

動作している Matplotlib を確認するには、新しいセルで以下のコードを実行し、前のラボで構築した機械学習モデルの ROC 曲線をプロットします。

from sklearn.metrics import roc_curve

fpr, tpr, _ = roc_curve(test_y, probabilities[:, 1])
plt.plot(fpr, tpr)
plt.plot([0, 1], [0, 1], color='grey', lw=1, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')

次の出力が表示されることを確認します。

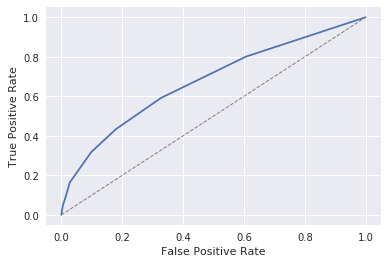
Matplotlib で生成された ROC 曲線

グラフの中央の点線は、正しい解答の取得確率が 50 対 50 であることを表します。青い曲線はモデルの精度を表します。さらに重要なのは、Jupyter ノートブックで Matplotlib を使用できるすべてのデモンストレーションでこのグラフが示されることです。

機械学習モデルを構築する理由は、フライトの到着が定刻であるか遅れるかを予測するためです。この演習では、フライトが定刻となる可能性を計算するために前のラボで構築した機械学習モデルを呼び出す Python 関数を記述します。その後、関数を使用してフライトをいくつか分析します。

新しいセルに次の関数定義を入力してから、セルを実行します。

def predict_delay(departure_date_time, origin, destination):
    from datetime import datetime

    try:
        departure_date_time_parsed = datetime.strptime(departure_date_time, '%d/%m/%Y %H:%M:%S')
    except ValueError as e:
        return 'Error parsing date/time - {}'.format(e)

    month = departure_date_time_parsed.month
    day = departure_date_time_parsed.day
    day_of_week = departure_date_time_parsed.isoweekday()
    hour = departure_date_time_parsed.hour

    origin = origin.upper()
    destination = destination.upper()

    input = [{'MONTH': month,
              'DAY': day,
              'DAY_OF_WEEK': day_of_week,
              'CRS_DEP_TIME': hour,
              'ORIGIN_ATL': 1 if origin == 'ATL' else 0,
              'ORIGIN_DTW': 1 if origin == 'DTW' else 0,
              'ORIGIN_JFK': 1 if origin == 'JFK' else 0,
              'ORIGIN_MSP': 1 if origin == 'MSP' else 0,
              'ORIGIN_SEA': 1 if origin == 'SEA' else 0,
              'DEST_ATL': 1 if destination == 'ATL' else 0,
              'DEST_DTW': 1 if destination == 'DTW' else 0,
              'DEST_JFK': 1 if destination == 'JFK' else 0,
              'DEST_MSP': 1 if destination == 'MSP' else 0,
              'DEST_SEA': 1 if destination == 'SEA' else 0 }]

    return model.predict_proba(pd.DataFrame(input))[0][0]

この関数では日時、出発地の空港コード、目的地の空港コードを入力として受け取り、フライトがその目的地に定刻に到着する確率を示す、0.0 から 1.0 の値を返します。前のラボで構築した機械学習モデルを使用して、確率を計算します。その後、モデルを呼び出すために、入力値を含む DataFrame を predict_proba に渡します。 DataFrame の構造は、以前使用した DataFrame の構造と完全に一致します。

Note

predict_delay 関数への日付入力では、国際日付形式である dd/mm/year が使用されます。

以下のコードを使用して、10 月 1 日の夜のニューヨークからアトランタへのフライトが定刻に到着する確率を計算します。入力する年はモデルでは使用されないため、重要ではありません。
```
predict_delay('1/10/2018 21:45:00', 'JFK', 'ATL')
```
出力に、定刻到着の可能性が 60% と示されていることを確認します。

フライトが定刻に到着するかどうかの予測
コードを変更し、1 日後の同じフライトが定刻に到着する確率を計算します。
```
predict_delay('2/10/2018 21:45:00', 'JFK', 'ATL')
```
このフライトが定刻に到着する可能性はどのくらいでしょうか。柔軟な旅行計画だったとしたら、旅行を 1 日延期することを検討しますか。
次はコードを変更し、アトランタからシアトルへの同じ日の朝のフライトが定刻に到着する確率を計算します。
```
predict_delay('2/10/2018 10:00:00', 'ATL', 'SEA')
```
このフライトが定刻に到着する可能性はありますか。

1 行のコードを使って、フライトが定刻となるか遅れる可能性があるかを予測する簡単な方法があります。他の日付、時刻、出発地、目的地で自由に試してください。しかし、結果は空港コードの ATL、DTW、JFK、MSP、SEA の場合にのみ意味があることに注意してください。モデルのトレーニングで使用されたのはこれらの空港コードのみであるためです。

次のコードを実行し、日の範囲で JFK から ATL への夜のフライトの定刻到着の確率をプロットとします。

import numpy as np

labels = ('Oct 1', 'Oct 2', 'Oct 3', 'Oct 4', 'Oct 5', 'Oct 6', 'Oct 7')
values = (predict_delay('1/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('2/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('3/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('4/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('5/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('6/10/2018 21:45:00', 'JFK', 'ATL'),
          predict_delay('7/10/2018 21:45:00', 'JFK', 'ATL'))
alabels = np.arange(len(labels))

plt.bar(alabels, values, align='center', alpha=0.5)
plt.xticks(alabels, labels)
plt.ylabel('Probability of On-Time Arrival')
plt.ylim((0.0, 1.0))

出力が次のようになることを確認します。

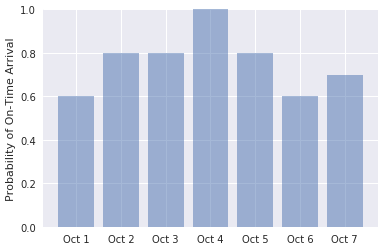
日付の範囲の定刻到着の確率
コードを変更し、4 月 10 日から 4 月 16 日までの午後 1 時 00 分に MSP に向けて JFK を出発するフライトの同様のグラフを生成します。前の手順の出力と比べてどうですか。
自分でコードを記述し、1 月 30 日の午前 9 時 00 分、正午、午後 3 時 00 分、午後 6 時 00 分、午後 9 時 00 分に ATL に向けて SEA を出発するフライトが定刻に到着する確率をグラフ化してみてください。出力が以下と一致することを確認します。

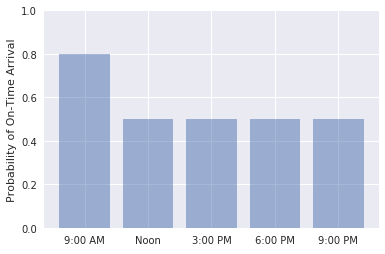
時刻の範囲の定刻到着の確率

Matplotlib を初めてお使いになる方で、さらに学習したい場合は、https://www.labri.fr/perso/nrougier/teaching/matplotlib/. の優れたチュートリアルを参照してください。Matplotlib について、ここよりはるかに 多くのことが示されています。それが、Python コミュニティで非常に人気がある 1 つの理由です。

演習 : モデルの出力を視覚化する

フィードバック