ROC 曲線を比較して最適化する
受信者操作特性 (ROC) 曲線を使用すると、モデルを相互に比較し、選択したモデルを調整することができます。 それを行う方法と理由について説明します。
モデルのチューニング
ROC 曲線の最も明白な用途は、最適なパフォーマンスが得られる決定のしきい値を選択することです。 このモデルでは、65% の確率でサンプルはハイカーである、といった確率が提供されることを思い出してください。 決定のしきい値は、それより上ではサンプルに true (ハイカー) が割り当てられる、またはそれより下では false (木) が割り当てられるポイントです。 決定しきい値が 50% の場合、65% は "true" (ハイカー) に割り当てられます。 しかし、決定しきい値が 70% の場合は、65% の確率は小さすぎるので、"false" (木) に割り当てられます。
前の演習では、ROC 曲線を作成するときに、決定しきい値だけを変更してモデルの動作を評価しました。 これを行うと、最適な結果が得られるしきい値を見つけることができます。
通常、最適な真陽性率 (TPR) と低い擬陽性率 (FPR) の両方を提供する単一のしきい値はありません。 つまり、最適なしきい値は、何を達成しようとしているかによって異なります。 たとえば、このシナリオでは、ハイカーが識別されずに雪崩が発生した場合、チームは救助が必要なことがわからないため、真陽性率を高くすることが非常に重要です。 ただし、トレードオフがあります。擬陽性率が高すぎると、単に存在しない人を救助するために、救助隊が何度も派遣される可能性があります。 他の状況では、擬陽性率がさらに重要であると見なされます。 たとえば、科学では擬陽性の結果に対する許容度が低くなります。 科学実験の擬陽性率が高い場合は、相反する結果がいつまでも収まらず、何が真実なのかを解明できません。
AUC を使用したモデルの比較
コスト関数と同様に、ROC 曲線を使用してモデルを相互に比較できます。 モデルの ROC 曲線は、さまざまな決定しきい値に対してモデルがどの程度うまく機能するかを示します。 最終的に、モデルで最も重要なのは、決定しきい値が 1 つだけである現実世界でのモデルのパフォーマンスです。 それではなぜ、使用することのないしきい値を使用してモデルを比較する必要があるのでしょうか。 これには 2 つの答えがあります。
まず、統計テストを実行するのと似て、ROC 曲線を特定の方法で比較すると、この特定のテスト セットで 1 つのモデルが優れた動作を示したことだけでなく、将来も優れたパフォーマンスが続く可能性があるかどうかもわかります。 これは、この学習資料の範囲外ですが、憶えておく価値があることです。
第 2 に、ROC 曲線を見ると、完全なしきい値を設定することにモデルがどれくらい依存するかが、ある程度わかります。 たとえば、決定しきい値が 0.9 のときにだけモデルが優れた動作を示し、この値より上か下では悪いような場合は、よい設計ではありません。 多くの場合、さまざまなしきい値で適切に機能するのが望ましいモデルであり、実際のデータがテスト セットと多少異なっていても、モデルのパフォーマンスが必ずしも低下しないことがわかります。
ROC を比較する方法
ROC を数値で比較する最も簡単な方法は、曲線下面積 (AUC) を使用することです。 文字どおり、これは曲線の下にあるグラフの面積です。 たとえば、前の演習の完全なモデルでは、AUC が 1 になります。
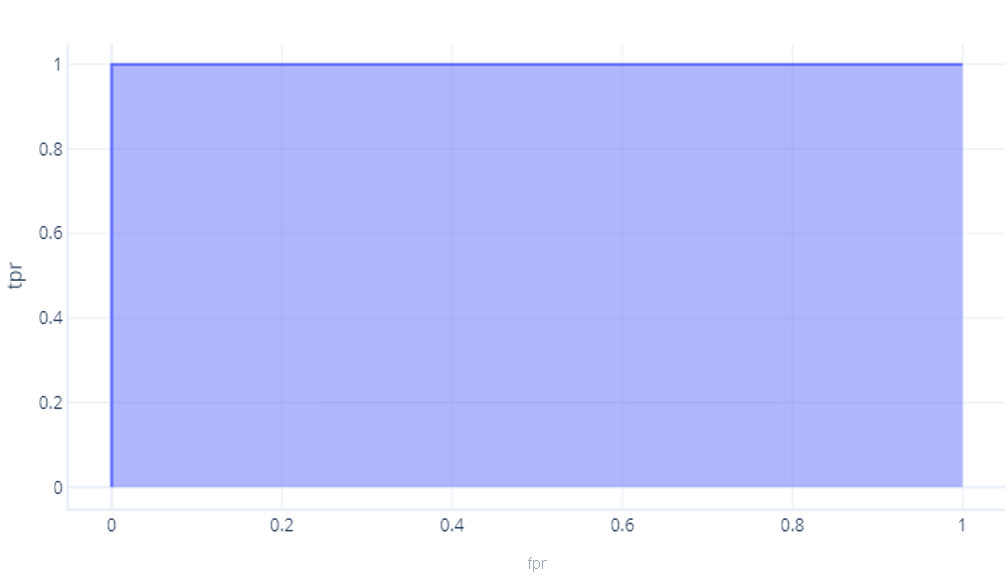
一方、確率が偶然と変わらないモデルでは、面積は約 0.5 になります。
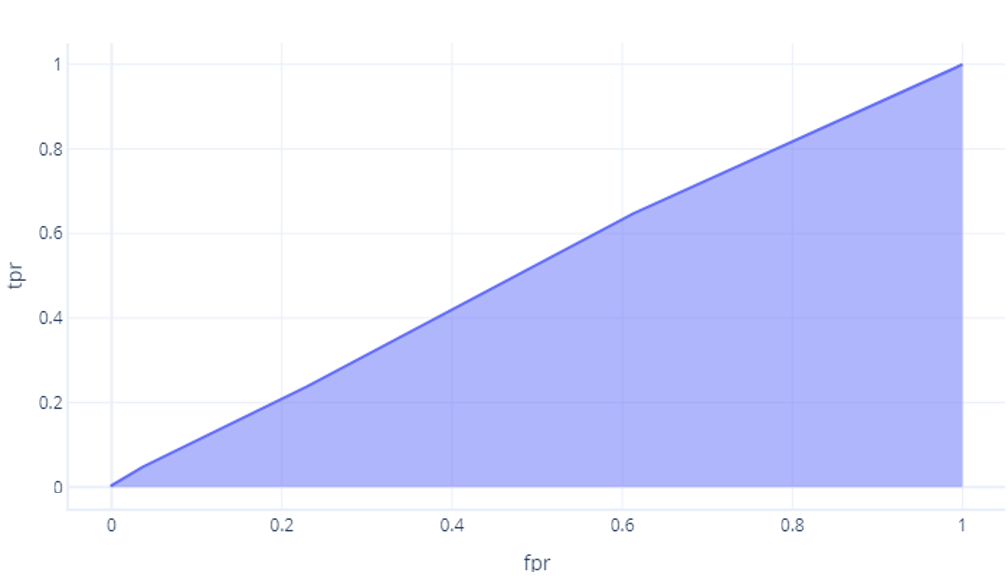
モデルが完璧に近くなるほど、この面積は大きくなります。 モデルの AUC が大きい場合は、さまざまなしきい値に対して適切に機能することがわかり、おそらく、優れたアーキテクチャを備え、適切にトレーニングされています。 これに対し、AUC が小さい (0.5 に近い) モデルはうまく機能しません。