混同行列

  • 4 分

データは、カテゴリ データ、または序数データ (順序を持つカテゴリ データ) のいずれかであると考えることができます。 混同行列は、カテゴリ モデルがどれだけ適切に動作しているかを評価するための手段です。 これらの動作方法に関するコンテキストのために、まず、連続データに関する知識を更新しましょう。 これを通して、混同行列が、既に馴染みのあるヒストグラムの拡張にすぎないことを確認できます。

連続データの分布

連続データを理解しようとする場合は通常、最初のステップとして、それが分布している状態を確認します。 次のヒストグラムについて考えます。

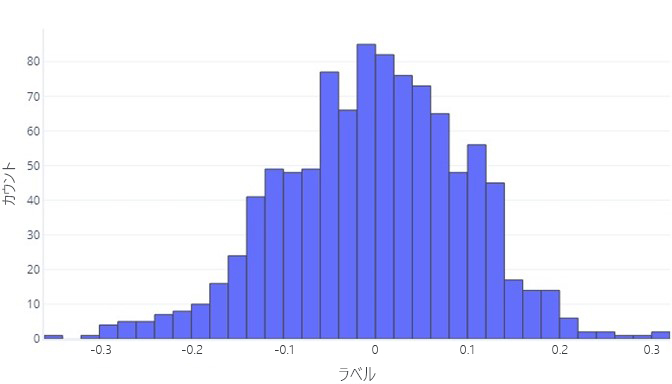
ラベルの分布を示すヒストグラム。

ラベルは平均して約 0 であり、ほとんどのデータポイントが -1 と 1 の間に収まることを確認できます。 これは対称形になっています。平均より小さい領域と大きい領域に、ほぼ同じ数が存在します。 必要な場合は、ヒストグラムではなく表を使用することもできますが、扱いにくくなる可能性があります。

カテゴリ データの分布

いくつかの点で、カテゴリ データは連続データとそれほど異なりません。 各ラベルの値が現れる頻度を評価するには、引き続きヒストグラムを生成できます。 たとえば、バイナリ ラベル (true/false) の頻度が次のようになることがあります。

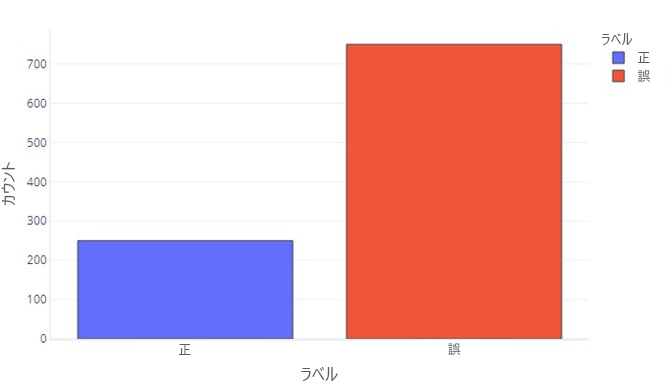
true ラベルより false ラベルの方が多いことを示す棒グラフ。

これは、ラベルが "false" であるサンプルが 750 件、ラベルが "true" であるサンプルが 250 件あることを示しています。

3 つのカテゴリのラベルも同様です。

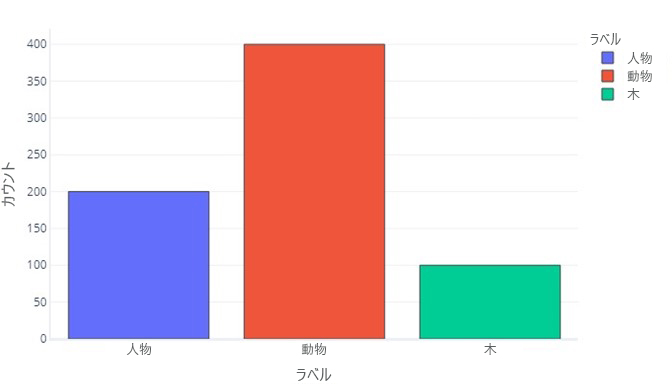
人間や木のラベルより動物のラベルの方が多いことを示す棒グラフ。

これは、"人間" であるサンプルが 200 件、"動物" であるサンプルが 400 件、"木" であるサンプルが 100 件存在することを示しています。

カテゴリ ラベルは単純であるため、多くの場合は、これらを簡単な表として示すことができます。 前の 2 つのグラフは次のようになります。

ラベル False True
Count 750 250

および

ラベル Person 動物 ツリー
Count 200 400 100

予測の調査

データ内の実際のラベルを調べるのと同様に、モデルが行う予測を調べることができます。 たとえば、テスト セットでは、モデルによって "false"が 700 回、"true" が 300 回予測されたことがわかります。

モデルの予測 Count
False 700
True 300

これにより、モデルが行っている予測に関する直接的な情報が提供されますが、これらのうちのどれが正しいかは示されません。 コスト関数を使用して、正しい応答が得られる頻度を理解することはできますが、コスト関数では、どの種類のエラーが発生しているかは示されません。 たとえば、モデルがすべての "true" 値を正しく推測する可能性はありますが、"false" と推測すべきときに "true" と推測する可能性もあります。

混同行列

モデルのパフォーマンスを理解するための鍵は、モデルの予測の表を実際のデータ ラベルの表と組み合わせることです。

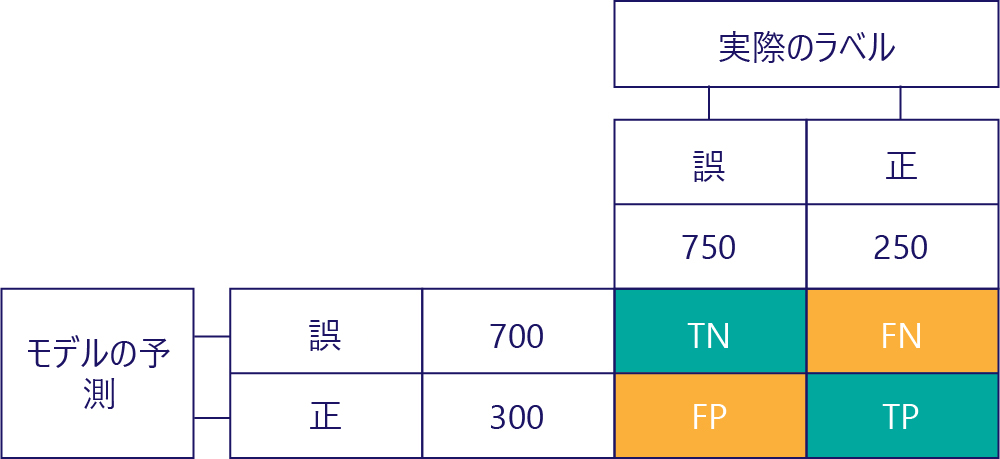
合計数が追加されている混同行列の図。

まだ入力されていない正方形は、混同行列と呼ばれます。

混同行列内の各セルはモデルのパフォーマンスに関する 1 つのことを示しています。 これらは、真陰性 (TN)、偽陰性 (FN)、擬陽性 (FP)、真陽性 (TP) です。

これらの頭字語を実際の値に置き換えて、これらを 1 つずつ説明しましょう。 青緑色の長方形は、モデルが正しい予測を行ったことを示し、オレンジ色の長方形は、モデルが間違った予測を行ったことを示します。

真陰性 (TN)

左上の値は、モデルが false を予測し、実際のラベルも false だった回数を示します。 つまり、これは、モデルが false を正しく予測した回数を示します。 たとえば、これが 500 回発生したとしてみましょう。

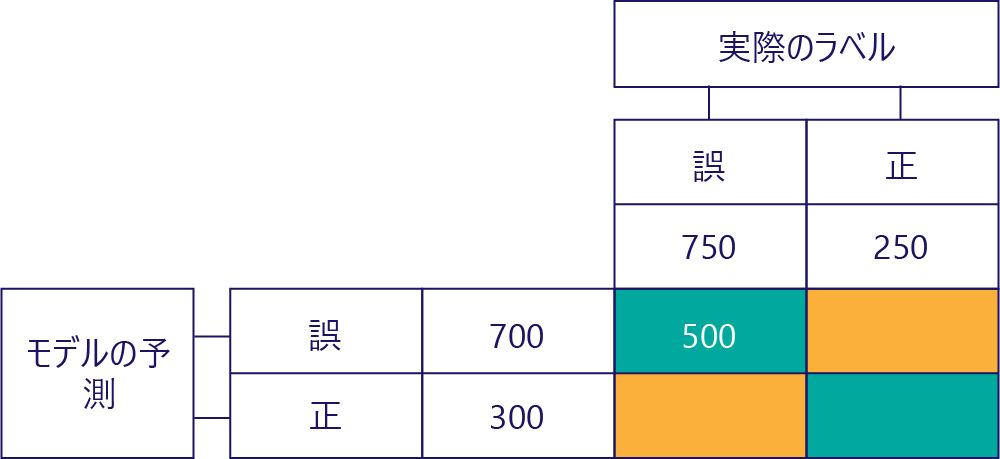
真陰性のみを示す、合計数が含まれていない混同行列の図。

偽陰性 (FN)

右上の値は、モデルは false を予測したが、実際のラベルは true だった回数を示しています。 これは 200 であることがわかっています。 方法はありますか。 モデルは false を 700 回予測し、その回数のうちの 500 回は正しく予測したためです。 そのため、間違って false を予測したことが 200 回あったに違いありません。

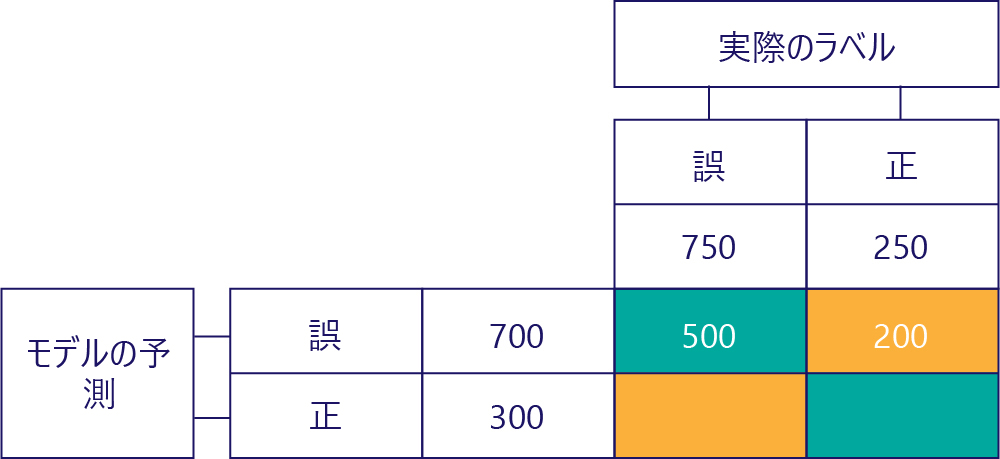
偽陰性のみを示す混同行列の図。

擬陽性 (FP)

左下の値は、擬陽性を保持しています。 これは、モデルは true を予測したが、実際のラベルは false だった回数を示しています。 false が正解だった回数は 750 回であったため、これは 250 件であることがわかりました。 これらの回数のうちの 500 が左上のセル (TN) に現れます。

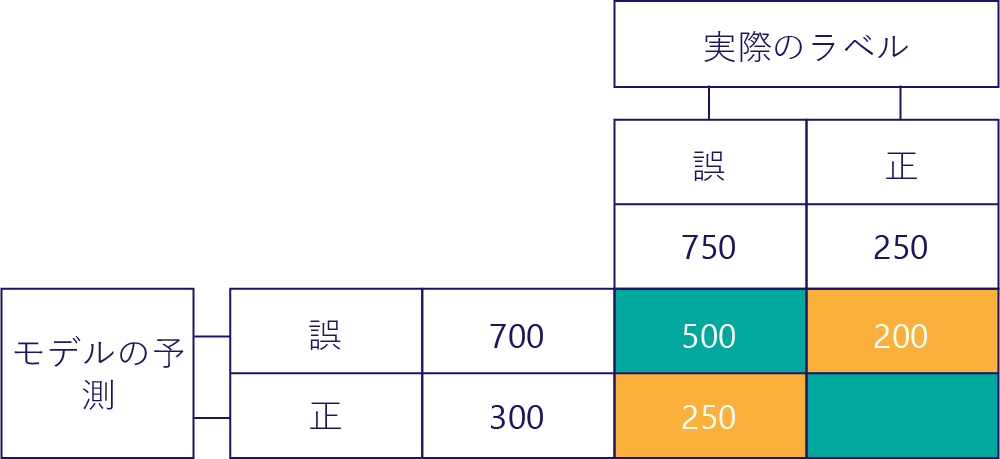
擬陽性も示す混同行列の図。

真陽性 (TP)

最後に、真陽性があります。 これは、モデルが true を正しく予測した回数です。 2 つの理由から、これは 50 であることがわかっています。 最初に、モデルは true を 300 回予測したが、250 回間違っていました (左下のセル)。 2 番目に、true が正しい答えだったことは 250 回ありましたが、モデルはそのうちの 200 回 false を予測しました。

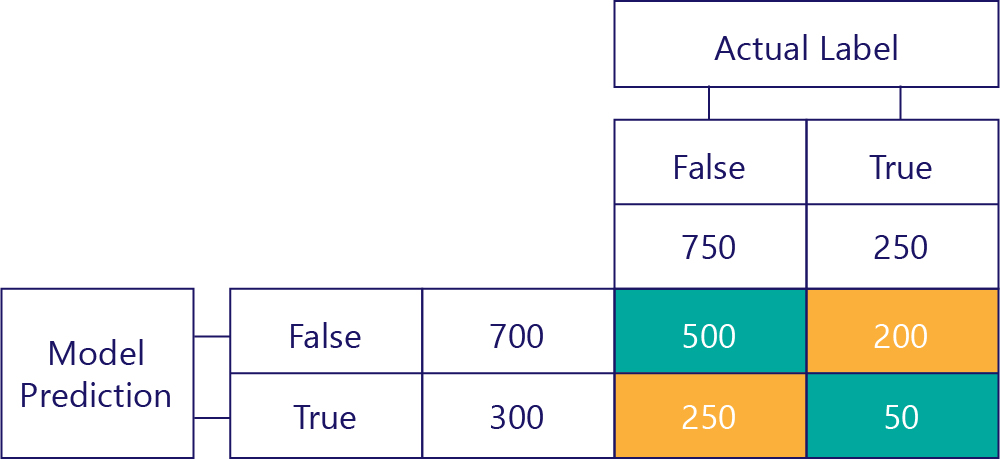
真陽性も示す混同行列の図。

最終的な行列

通常は、次のように混同行列を少し簡略化します。

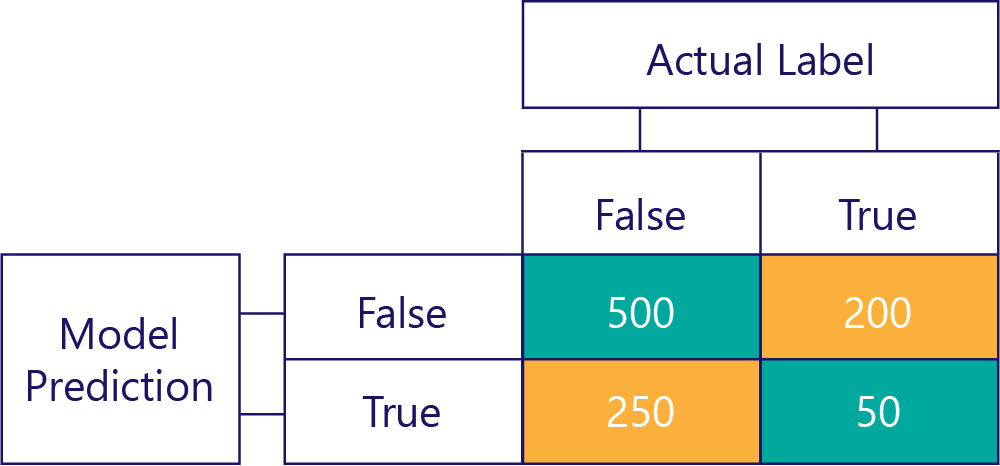
簡略化された混同行列の図。

ここでは、モデルが正しい予測を行った場合を強調表示するためにセルを色分けしています。 この行列からは、モデルが特定の種類の予測を行った頻度だけでなく、これらの予測が正しかった頻度または間違っていた頻度もわかります。

混同行列は、さらに多くのラベルがある場合にも構築できます。 たとえば、人間/動物/木の例の場合は、次のような行列が得られることがあります。

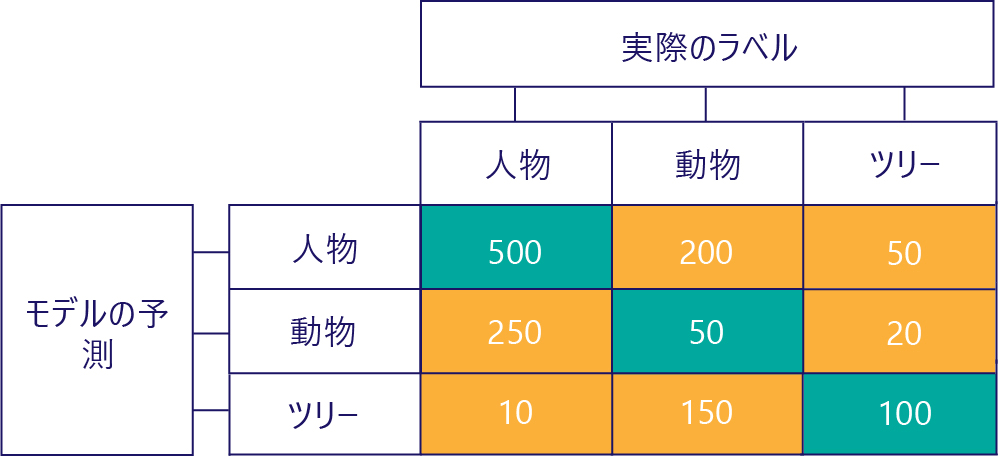
3 つのラベル (人間、動物、木) が含まれている拡張された混同行列の図。

3 つのカテゴリがある場合は、真陽性などのメトリックが適用されなくなりますが、モデルが特定の種類の間違いを犯した頻度は引き続き正確に確認できます。 たとえば、実際の正しい結果は "動物" だったが、モデルは "人間" を予測したことが 200 回あったことを確認できます。