量子コンピューティングにおける重ね合わせとは
前のユニットの猫が量子猫の場合、量子猫と箱システムの状態は同じとなり、箱に関して、その位置で量子猫を見つける確率によって重み付けされた、量子猫の 6 つの異なる位置の総和となります。 唯一の違いは、古典的な猫は 6 つの可能な位置の 1 つ (のみ) に存在しますが、量子猫は同時に 6 つの位置すべてに存在する可能性があるということです。
古典的な世界では、オブジェクトは一度に 1 つの状態でしかいられません。 しかし、量子の世界では、量子粒子を同時に複数の状態にすることができます。 この現象が重ね合わせと呼ばれます。
量子コンピューティングでは、量子猫は使用されず、量子ビットが使用されます。 "qubit" という単語は "quantum bit" (量子ビット) を意味します。 情報の基本単位がビットである従来のコンピューティングと同様に、量子コンピューティングでは基本的な情報の単位は量子ビットになります。 ビットが 0 と 1 という 2 つの実現可能な値を取ることができるのと同様に、量子ビットは、2 つの実現可能な状態を取ることができる何らかの量子粒子です。 たとえば、量子ビットは、2 方向に偏光できる光子や、2 つのエネルギー レベルを取ることができる電子にすることができます。
量子ビットで重ね合わせはどのように表しますか? 特定の状態で量子ビットを見つける確率はどれくらいですか?
量子ビットで重ね合わせはどのように表しますか?
量子ビットは、2 つの可能な位置または状態を持つ量子粒子を表します。 従来のビットに似ていますが、量子ビットの量子状態は $0$ と $1$ とも呼ばれます。 量子ビットは、状態 $0$、状態 $1$、および両方の状態の重ね合わせにすることができます。 この重ね合わせはどのように表しますか?
中央の点が円の中心になるように、円および縦軸と横軸を描画するとします。 状態 $0$ は縦軸の上方の位置に配置され、状態 $1$ は下方の位置に配置されます。
この表現はどのように記述できますか? 状態 $0$ は上向きの矢印またはベクトルになり、状態 $1$ は下向きのベクトルになります。 従来のビットは、上または下のいずれかを指すベクトルになりますが、別の方向を指すことはありません。
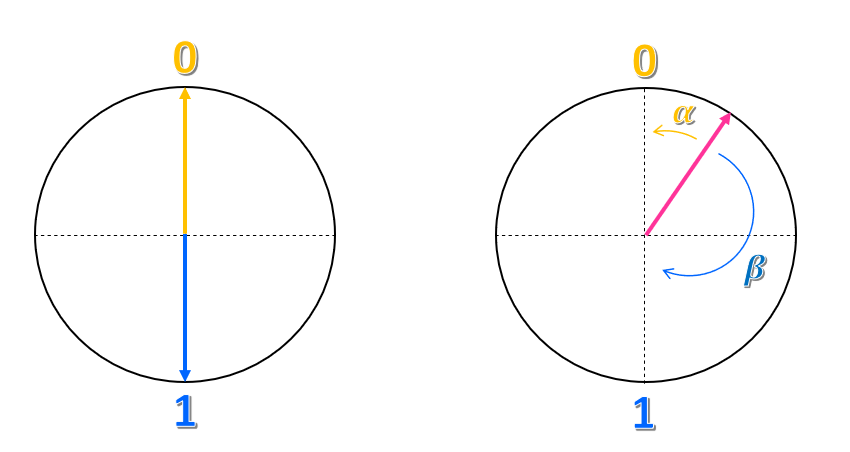
円の他の位置はどうなりますか? その状態はどのように表しますか? 平面内の座標と同様に、2 つの状態 $0$ と $1$ の組み合わせとして表すことができます。 たとえば、ベクトルが状態 $0$ からどれだけ近いかを取得し、その角度を $\alpha$ と呼び、状態 $1$ からどれだけ近いかを取得し、その角度を $\beta$ と呼びます。 この状態を $\alpha 0 + \beta 1 $ と表すことができます。 この状態が、状態 $0$ と $1$ の重ね合わせです。
猫と箱の例と同様に、量子ビットのグローバルな状態は、個々の状態 $0$ と $1$ の合計であり、その状態の量子ビットを見つける確率 $\alpha$ と $\beta $ で重み付けされます。
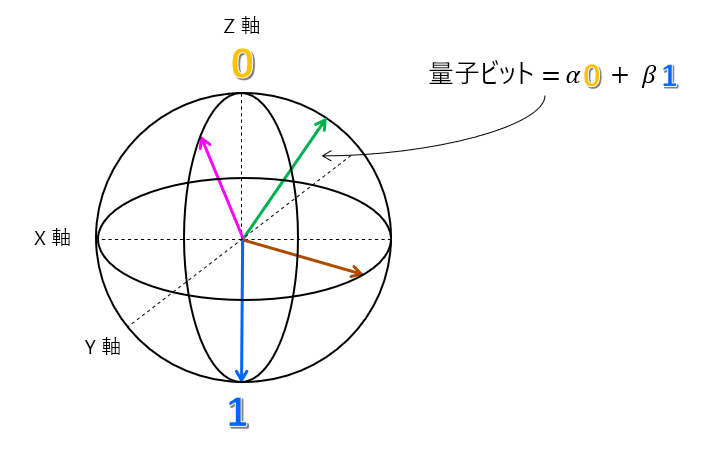
量子ビットのこの表現は正確であり、ブロッホ球と呼ばれます。
ヒント
ブロッホ球は、量子ビットに対して実行できる演算を、基準軸の 1 つを中心とした回転として表すことができる強力なツールです。 量子計算を一連の回転として考えることは説得力のある直感的洞察ですが、この洞察を利用してアルゴリズムを設計し、記述することは難易度が高い作業です。 Q# は、このような回転を記述するための言語を提供することで、この問題を軽減します。
状態で量子ビットを見つける確率はどれくらいですか?
前のユニットの猫と箱の例と同様に、量子ビットのグローバルな状態は、個々の状態 $0$ と $1$ の合計であり、その状態の量子ビットを見つける確率 $\alpha$ と $\beta $ で重み付けされます。 数値 $\alpha$ と $\beta$ は、量子ビット状態が状態 $0$ と $1$ に対してどれほど "近い" かを表します。 では、$\alpha$ と $\beta$ は、状態 $0$ または $1$ の量子ビットを見つける確率になりますか? そうとも限りません。
数値 $\alpha$ と $\beta$ は、各状態の確率振幅です。 これらの絶対値 ($|\alpha|^2$ など) は、対応する確率になります。 たとえば、状態 $0$ を観測する確率は $|\alpha|^2$ で、状態 $1$ を観測する確率は $|\beta|^2$ です。
数値 $\alpha$ と $\beta$ は、正の値、負の値、または複素数にもなります。 ただし、有効な量子の重ね合わせでは、すべての確率の合計が 1 になる必要があります。つまり、$|\alpha|^2+|\beta|^2=1$ です。 この制約は、"正規化条件" と呼ばれることがあります。 正規化条件は、測定時に常に結果を取得するという事実と考えることができます。したがって、可能なすべての結果を測定する確率は合計で 1 になる必要があります。