エンタングルメントを使用して情報を送信する方法
前のユニットでは、量子もつれが量子通信の優れたリソースになる可能性があることを学習しました。 このユニットでは、もつれの最も有名なアプリケーションの 1 つである量子テレポーテーション プロトコルについて説明します。
テレポーテーションでは、量子ビットの状態を、ある場所から別の場所に転送するのにもつれが使用されます。 量子ビットの状態は別の量子ビットに転送されますが、量子ビット自体が物理的に移動することはありません。 これを忘れないことが重要です。 量子ビットの状態の情報は、メッセージ量子ビットの情報を書き込む容器として使用されている別の量子ビットに転送されます。
テレポーテーション プロトコルでは、もつれと従来の通信の組み合わせが使用されます。 テレポーテーション プロトコルでは送信者が測定結果を受信者に伝える必要があります。このため、従来型の通信は重要です。 つまり、テレポーテーションでは、光の速度よりも速く情報を送信することはできません。 送信者と受信者の間の従来型の通信は、光の速度によって制限されます。
量子テレポーテーションのプロトコルについて確認してみましょう。
量子テレポーテーションのプロトコル
Alice と Bob は同じ会社で働いています。 Alice はシアトルを拠点とし、Bob はロサンゼルスを拠点としています。 2 人が取り組んでいるプロジェクトでは、量子情報を共有する必要があります。 そこで量子テレポーテーションを使って、量子情報を送信し合うことにしました。
初期設定
Alice と Bob はそれぞれ量子ビットを持っています。その量子ビットは、以前に準備されたエンタングル ペアの一部です。 エンタングル ペアはベル状態です。その状態を次に示します
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice には "メッセージ量子ビット" と呼ばれる追加の量子ビットがあり、この量子ビットを Bob に送信したいと考えています。 Alice が Bob にテレポートする必要があるのは、不明な状態のメッセージ量子ビットです。 メッセージ量子ビットの状態は次のとおりです
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m$$
ここで、$\alpha$ と $\beta$ は複素数です。
Alice と Bob の 3 つの量子ビットのグローバル状態は次のとおりです
$$\ket{\text{グローバル}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$
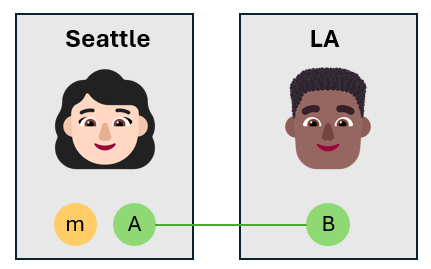
Alice はメッセージ量子ビットを自分の量子ビットとエンタングル状態にする
Alice はメッセージ量子ビットを受け取り、CNOT ゲートを使用して、それを、自分の量子ビット $A$ とエンタングル状態にします。 メッセージ量子ビットはコントロール量子ビットで、Alice の量子ビットは target 量子ビットです。 これにより、3 量子ビット エンタングル状態が作成されます。
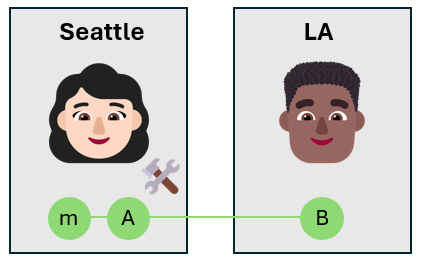
メッセージ量子ビットは不明な状態 $\alpha\ket{0}_m + \beta\ket{1}_m$ であるため、CNOT ゲートの適用後、Alice の量子ビットは 4 つのベル状態の重ね合わせになります。 3 つの量子ビットのグローバル状態は次のとおりです
$$\ket{\text{グローバル}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$
$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$
$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Alice と Bob の量子ビットのグローバル状態は、4 つの可能な状態の重ね合わせです。
ヒント
3 つの量子ビットのグローバル状態が上記の状態であることを確認することをお勧めします。 これを行うには、CNOT ゲートを、メッセージ量子ビットと Alice の量子ビットに適用してから、3 つの量子ビットの状態を拡張します。
Alice が量子ビットを測定する
その後、Alice はメッセージ量子ビットと自身の量子ビットを測定します。 $Z$ 基底の量子ビットを通常のように測定するのではなく、"Bell 基底" を選択します。 ベル基底は、$\lbrace \ket{\phi^+}、\ket{\phi^-}、\ket{\psi^+}、\ket{\psi^-} \rbrace$ の 4 つのベル状態で構成されます。
Alice は、メッセージ量子ビットと自身の量子ビットをベル基底で測定することで、自身の量子ビットを、4 つのベル状態のいずれかに投影します。 3 つの量子ビットはエンタングル状態であるため、測定結果は関連付けられています。 Alice が自身の量子ビットを測定すると、Bob の量子ビットも相関状態に投影されます。
たとえば、Alice が自身の量子ビットを測定し、状態 $\ket{\phi^-}$ を観察した場合、Bob の量子ビットは、状態 $\alpha\ket{0}_B - \beta\ket{1}_B$ に投影されます。
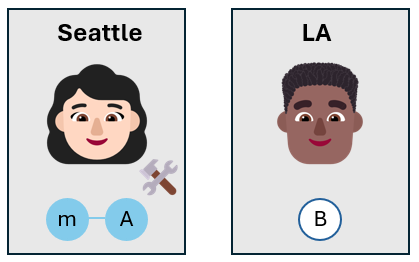
Alice が Bob を呼び出す
Alice が Bob を呼び出し、測定の結果を伝えます。 彼女は、電話やテキスト メッセージなどの従来の通信チャネルを使用します。
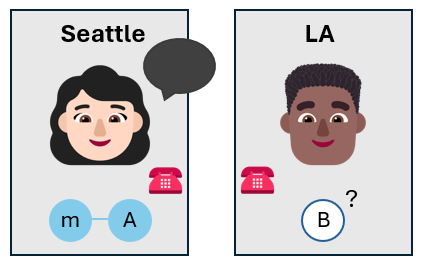
Bob は、自身の量子の状態を、測定せずに、認識するようになりました。 Bob の量子ビットの状態は、Alice がテレポートしたかったメッセージ量子ビットの状態と同じではない可能性がありますが、それに近い状態です。
Bob が量子演算を適用する
次に、Bob は、特定の量子演算を自身の量子ビットに適用することで、メッセージ量子ビットの元の状態を復元できます。 Bob が実行する演算は、Alice が電話で彼に伝えた内容によって異なります。
実行する演算は、パウリ $X$ ゲート、パウリ $Z$ ゲート、両方、またはなしです。
たとえば、Alice の測定結果が $\ket{\phi^-}$ の場合、Bob は、自身の量子ビットが状態 $(\alpha\ket{0}_B - \beta\ket{1}_B)$ であることを認識します。 彼がメッセージ量子ビットの元の状態を復元するには、パウリ Z ゲートを適用するだけで済みます。
| Alice の測定結果 | Bob が適用する演算 |
|---|---|
| $\ket{\phi^+}$ | 操作は実行されません |
| $\ket{\phi^-}$ | パウリ Z ゲート |
| $\ket{\psi^+}$ | パウリ X ゲート |
| $\ket{\psi^-}$ | パウリ X ゲートの後にパウリ Z ゲート |
この最後の演算により、メッセージ量子ビットの状態が、Bob の量子ビットに効果的にテレポートされます。 ミッションは完了です。
重要
量子ビットに演算を適用することは、それを測定することと同じでありません。 Bob が演算を適用するとき、その量子ビットを測定していません。 彼は量子ビットの状態を変更する量子演算を適用しますが、折りたたむことはありません。