演習 - Q# を使用して量子もつれを作成する

7 分

前のユニットでは、量子もつれとベル状態の概念について学習しました。

ここでは、Q# と Azure Quantum Development Kit を使って量子もつれを作成してみましょう。もつれを作成するには、アダマールゲートと制御 NOT (CNOT) ゲートの 2 つの量子演算を適用する必要があります。

制御 NOT (CNOT) 操作

2 つの量子ビットがもつれるとき、1 つの量子ビットの状態は、もう一方の量子ビットの状態に依存します。このため、2 つの量子ビットをもつれさせるには、両方の量子ビットに同時に作用する操作が必要です。これは、"複数量子ビット演算" と呼ばれます。

量子もつれを作成するには、"制御 NOT" を表す複数量子ビットの CNOT 演算が必要です。この操作は 2 つの量子ビットを入力として受け取ります。1 つは制御量子ビットとして機能し、もう 1 つは target 量子ビットです。 CNOT 演算は、最初の量子ビット (制御量子ビット) の状態が $|1\rangle$ の場合にのみ、2 番めの量子ビット (target 量子ビット) の状態を反転します。

入力	出力
$\ket{00}$	$\ket{00}$
$\ket{01}$	$\ket{01}$
$\ket{10}$	$\ket{11}$
$\ket{11}$	$\ket{10}$

Q# では、CNOT 演算は 2 つの量子ビットの配列に作用し、最初の量子ビットが One の場合に 2 番めの量子ビットを反転します。

CNOT 操作を使用したもつれ

アダマール (H) 演算と制御 NOT (CNOT) 演算を適用することで、状態 $|00\rangle$ の 2 つの量子ビットを、ベル状態 $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$ に変換できます。

その仕組みを次に示します。

状態 $|00\rangle$ の 2 つの量子ビットを使用します。最初の量子ビットが制御量子ビットで、2 番めの量子ビットが target 量子ビットです。
$H$ を適用して、制御量子ビットにのみ重ね合わせ状態を作成します。

$$H |0_c\rangle=\frac{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)$$

ヒント

下付き文字 ${}_c$ と ${}_t$ は、制御量子ビットと target 量子ビットを示します。
$CNOT$ 演算子を重ね合わせ状態の制御量子ビットと、$| 0_t \rangle$ 状態の target 量子ビットに適用します。

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}+\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}+|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} + CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}+\ket{1_c 1_t})$$

新しい Q# ファイルを作成する

Visual Studio Code を開きます。
[ファイル] > [新しいテキストファイル] の順に選択し、ファイルを Main.qs として保存します。
[表示] -> [コマンドパレット] を選択し、「Q#: Azure Quantum QIR target プロファイルを設定する」と入力します。 Enter キーを押します。
Q#:Unrestricted を選択します。

ベル状態 $\ket{\phi^+}$ を作成する

ベル状態 $\ket{\phi^+}=\frac1{\sqrt2}(|00\rangle+|11\rangle)$ の作成から始めましょう。

最初に、DumpMachine 関数が含まれる Microsoft.Quantum.Diagnostics 名前空間を標準ライブラリからインポートする必要があります。この関数は、量子ビットの現在の状態を示します。次の Q# コードをコピーして、Main.qs ファイルに貼り付けます。
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;
```
ヒント

Microsoft.Quantum を Std に置き換えて、標準ライブラリをインポートすることもできます。たとえば、import Std.Diagnostics.* は、import Microsoft.Quantum.Diagnostics.* と同じです。

量子ビットの測定結果である 2 つの Result 型の値を返す Main 演算を作成します。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    // Your code goes here
}

Main 演算内では、q1 と q2 の 2 つの量子ビットを割り当てます。それをもつれさせます。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());
}

1 番目の量子ビット q1 にアダマールゲート H を適用して、それを重ね合わせ状態にします。次に、CNOT 演算を使って 2 つの量子ビットをもつれさせます。
```
import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
}
```

DumpMachine 関数を使って、量子ビットの現在の状態を表示します。これは、量子ビットの測定と同じことではありません。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();
}

M 演算を使って量子ビットを測定し、結果を m1 と m2 に格納します。次に、Reset 演算を使って量子ビットをリセットします。 Q# では、量子ビットを常に $|0\rangle$ 状態にリセットする必要があります。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {

    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);
    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

}

最後に、return ステートメントで量子ビットの測定結果を返します。 Main.qs ファイルは次のようになります。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

組み込みのシミュレーターでプログラムを実行するには、Main 演算の上の [実行] をクリックするか、Ctrl+F5 キーを押します。出力がデバッグコンソールに表示されます。
測定結果には相関関係があるため、プログラムの終了時に、(Zero, Zero) または (One, One) の結果を等しい確率で取得します。
Main 演算の上にあるコマンドの一覧で Circuit をクリックすると、回路図を視覚化できます。この回路図は、最初の量子ビットにアダマールゲートが適用され、両方の量子ビットに CNOT ゲートが適用されたことを示しています。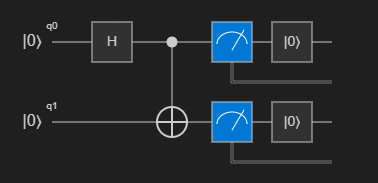

他のベル状態を作成する

他のベル状態を作成するには、量子ビットに追加のパウリ $X$ 演算とパウリ $Z$ 演算を適用する必要があります。

たとえば、ベル状態 $\ket{\phi^-}=\frac1{\sqrt2}(|00\rangle-|11\rangle)$ を作成するために、制御量子ビットにアダマールゲートを適用してから、パウリ $Z$ 演算を適用できます。 $Z$ 操作は、状態 $\ket{+}$ を $\ket{-}$ に反転します。

ヒント

状態 $\frac{{1}{\sqrt{2}}(|0\rangle+|1\rangle)$ と $\frac{1}{\sqrt{{2}}(|0\rangle -|1\rangle)$ は、それぞれ $\ket{+}$ と $\ket{{-}$ とも表されます。

その仕組みを次に示します。

状態 $|00\rangle$ の 2 つの量子ビットを使用します。
$H$ を適用して、制御量子ビットにのみ重ね合わせ状態を作成します。

$$H |0_c\rangle=\frac{{1}{\sqrt{2}}(|0_c\rangle+|1_c\rangle) =\ket{+}_c$$
制御量子ビットに $Z$ 演算を適用します。

$$Z \frac{{1}{\sqrt{{2}}(|0_c\rangle+|1_c\rangle)=\frac{1}{\sqrt{{2}}(|0_c\rangle-|1_c\rangle)=\ket{{-}_c$$
$CNOT$ 演算子を制御量子ビットと、$| 0_t \rangle$ 状態の target 量子ビットに適用します。

$$ CNOT \frac{1}{\sqrt{2}}(\ket{0_c}-\ket{1_c})\ket{0}_t = CNOT \frac{1}{\sqrt2}(\ket{0_c 0_t}-|\ket{1_c 0_t})=$$$$=\frac{{1}{\sqrt2}(CNOT \ket{0_c 0_t} - CNOT \ket{1_c 0_t})=$$$$=\frac{1}{\sqrt2}(\ket{0_c 0_t}-\ket{1_c 1_t})$$

同様に、量子ビットにパウリ $X$ 演算とパウリ $Z$ 演算を適用することで、ベル状態 $\ket{\psi^+}$ と $\ket{\psi^-}$ を作成できます。

ベル状態 $\ket{\psi^+}=\frac1{\sqrt2}(|01\rangle+|10\rangle)$ は、target 量子ビットにアダマールゲートを適用してから、パウリ $X$ 演算を適用することで作成できます。
ベル状態 $\ket{\psi^-}=\frac1{\sqrt2}(|01\rangle-|10\rangle)$ は、制御量子ビットにパウリ $Z$ を適用し、target 量子ビットにアダマールゲートを適用してから、パウリ $X$ を適用することで作成できます。

Q# でベル状態 $\ket{\phi^-}$ を作成する

Q# コードを変更して、ベル状態 $\ket{\phi^-}$ を作成します。 Main.qs ファイルは次のようになります。

import Microsoft.Quantum.Diagnostics.*; // Aka Std.Diagnostics.*;

operation Main() : (Result, Result) {
    use (q1, q2) = (Qubit(), Qubit());

    H(q1);
    Z(q1); // Apply the Pauli Z operation to the control qubit
    CNOT(q1, q2);

    DumpMachine();

    let (m1, m2) = (M(q1), M(q2));
    Reset(q1);
    Reset(q2);

    return (m1, m2);
}

組み込みのシミュレーターでプログラムを実行するには、Main 演算の上の [実行] をクリックするか、Ctrl+F5 キーを押します。出力がデバッグコンソールに表示されます。
Main 演算の上にあるコマンドの一覧で Circuit をクリックすると、回路図を視覚化できます。この回路図は、1 番目の量子ビットにアダマールゲートが適用され、1 番目の量子ビットにパウリ $Z$ ゲートが適用されて、両方の量子ビットに CNOT ゲートが適用されたことを示しています。

次のユニットでは、もつれを使用して量子情報をテレポートする方法を学習します。