3 つの種類のベジエ曲線

[アーティクル]
05/25/2017

SkiaSharp を使用して 3 次、2 次、円錐ベジエ曲線をレンダリングする方法について説明します

ベジエ曲線は、自動車会社ルノーのフランス人エンジニアであるピエール・ベジエ (1910-1999) にちなんだ名前で、コンピューターを使用した車体設計にこの曲線を使用しました。

ベジエ曲線は、インタラクティブな設計に適していることで知られています。うまく機能し (つまり、曲線が無限や扱いにくくなる特異点がない)、一般に美しい形状を作り出します。

ベジエ曲線のサンプル

コンピューターベースのフォントの文字アウトラインは、通常、ベジエ曲線で定義されます。

ベジエ曲線に関するウィキペディアの記事には、いくつかの有用な背景情報が記載されています。 "ベジエ曲線" という用語は、実際には類似した曲線のファミリを指します。 SkiaSharp は、"3 次曲線"、"2 次曲線"、"円錐曲線" と呼ばれる 3 種類のベジエ曲線をサポートしています。円錐曲線は "有理 2 次曲線" とも呼ばれます。

3 次ベジエ曲線

3 次曲線は、ほとんどの開発者がベジエ曲線の対象が現れるタイミングとして思い当たるベジエ曲線の種類です。

SKPath オブジェクトに 3 次ベジエ曲線を追加するには、3 つの SKPoint パラメーターを持つ CubicTo メソッドを使用するか、別の x および y パラメーターを持つ CubicTo オーバーロードを使用します。

public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)

public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)

この曲線は、輪郭の現在の点から始まります。完全な 3 次ベジエ曲線は、次の 4 つの点で定義されます。

始点: 輪郭の現在の点、または MoveTo が呼び出されていない場合は (0, 0)
1 つ目の制御点: CubicTo 呼び出しの point1
2 つ目の制御点: CubicTo 呼び出しの point2
終点: CubicTo 呼び出しの point3

結果として生成される曲線は始点から始まり、終点で終了します。一般に、曲線は 2 つの制御点を通過しません。そうではなく、制御点は磁石のように機能し、曲線を引き寄せます。

3 次ベジエ曲線に慣れる最善の方法は試してみることです。これが、InteractivePage から派生した [ベジエ曲線] ページの目的です。 BezierCurvePage.xaml ファイルは、SKCanvasView と TouchEffect のインスタンスを作成します。 BezierCurvePage.xaml.cs 分離コードファイルは、コンストラクターに 4 つの TouchPoint オブジェクトを作成します。 PaintSurface イベントハンドラーは、4 つの TouchPoint オブジェクトに基づいてベジエ曲線をレンダリングする SKPath を作成し、制御点から終点までの接線を点線で描画します。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with cubic Bezier curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.CubicTo(touchPoints[1].Center,
                     touchPoints[2].Center,
                     touchPoints[3].Center);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[2].Center.X,
                    touchPoints[2].Center.Y,
                    touchPoints[3].Center.X,
                    touchPoints[3].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
       touchPoint.Paint(canvas);
    }
}

実行結果は次のようになります。

数学的には、この曲線は 3 次多項式です。曲線は、最大 3 点で直線と交差します。始点では、曲線は常に、始点から 1 つ目の制御点までの直線と同じ方向に接します。終点では、曲線は常に、2 つ目の制御点から終点までの直線と同じ方向に接します。

3 次ベジエ曲線は常に、4 点を結ぶ凸四辺形によってバインドされます。これは "凸包" と呼ばれます。制御点が始点と終点の間の直線上にある場合、ベジエ曲線は直線としてレンダリングされます。ただし、3 つ目のスクリーンショットが示すように、曲線自体を交差させることもできます。

パスの輪郭には接続された複数の 3 次ベジエ曲線を含めることができますが、次の 3 点が同一直線上 (つまり 1 つの直線上) にある場合にのみ、2 つの 3 次ベジエ曲線は滑らかに接続されます。

1 つ目の曲線の 2 つ目の制御点
1 つ目の曲線の終点 (2 つ目の曲線の始点でもあります)
2 つ目の曲線の 1 つ目の制御点

SVG パスデータに関する次の記事では、滑らかに接続されたベジエ曲線を簡単に定義する機能について説明します。

3 次ベジエ曲線をレンダリングする基になる媒介変数表示方程式を知ると便利な場合があります。 t の範囲を 0 から 1 までとすると、媒介変数表示方程式は次のとおりになります。

x(t) = (1 – t)³x₀ + 3t(1 – t)²x₁ + 3t²(1 – t)x₂ + t³x₃

y(t) = (1 – t)³y₀ + 3t(1 – t)²y₁ + 3t²(1 – t)y₂ + t³y₃

最大指数が 3 であることで、これらが 3 次多項式であることが確認できます。 t が 0 の場合は、点が (x₀,y₀) (始点) であり、t が 1 の場合は、点が (x₃, y₃) (終点) であることが簡単に確認できます。始点の近く (t の値が小さい) では、1 つ目の制御点 (x₁、y₁) が強力な効果を持ち、終点の近く ('t' の値が大きい) では、2 つ目の制御点 (x₂、 y₂) が強い効果を持ちます。

円弧に対するベジエ曲線近似

ベジエ曲線を使用して円弧をレンダリングすると便利な場合があります。3 次ベジエ曲線は、4 分の 1 の円まで円弧を非常にうまく近似できるため、接続された 4 つのベジエ曲線で円全体を定義できます。この近似は、25 年以上前に公開された 2 つの記事で説明されています。

Tor Dokken およびその他、「曲率が連続したベジエ曲線による円の良好な近似」、Computer Aided Geometric Design 7 (1990)、33-41

Michael Goldapp、「3 次多項式による円弧の近似」、Computer Aided Geometric Design 8 (1991)、227-238

次の図は、円弧を近似するベジエ曲線 (赤) を定義する、pto、pt1、pt2、pt3 という名前の 4 点を示しています。

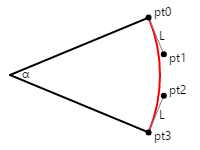
ベジエ曲線を使用した円弧の近似

始点と終点から制御点までの線は、円とベジエ曲線に接しており、長さは L です。上記で引用した 1 つ目の記事では、L の長さが次のように計算される場合に、ベジエ曲線が円弧を最も近似することを示しています。

L = 4 × tan(α / 4) / 3

この図の角度は 45 度であるため、L は 0.265 になります。コードでは、その値に円の目的の半径が乗算されます。

[Bezier Circular Arc] (ベジエ円弧) ページでは、ベジエ曲線を定義して、最大 180 度の角度の円弧を近似することができます。 BezierCircularArcPage.xaml ファイルは、角度を選択するための SKCanvasView と Slider のインスタンスを作成します。 BezierCircularArgPage.xaml.cs 分離コードファイルの PaintSurface イベントハンドラーは、変換を使用して、(0, 0) 点をキャンバスの中心に設定します。比較のためにその点を中心とする円を描画し、ベジエ曲線の 2 つの制御点を計算します。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Translate to center
    canvas.Translate(info.Width / 2, info.Height / 2);

    // Draw the circle
    float radius = Math.Min(info.Width, info.Height) / 3;
    canvas.DrawCircle(0, 0, radius, blackStroke);

    // Get the value of the Slider
    float angle = (float)angleSlider.Value;

    // Calculate length of control point line
    float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;

    // Calculate sin and cosine for half that angle
    float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
    float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);

    // Find the end points
    SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
    SKPoint point3 = new SKPoint(radius * sin, radius * cos);

    // Find the control points
    SKPoint point0Normalized = Normalize(point0);
    SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
                                          -length * point0Normalized.X);

    SKPoint point3Normalized = Normalize(point3);
    SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
                                          length * point3Normalized.X);

    // Draw the points
    canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
    canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
    canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
    canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);

    // Draw the tangent lines
    canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
    canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);

    // Draw the Bezier curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(point0);
        path.CubicTo(point1, point2, point3);
        canvas.DrawPath(path, redStroke);
    }
}

// Vector methods
SKPoint Normalize(SKPoint v)
{
    float magnitude = Magnitude(v);
    return new SKPoint(v.X / magnitude, v.Y / magnitude);
}

float Magnitude(SKPoint v)
{
    return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}

始点と終点 (point0 および point3) は、円の法線媒介変数表示方程式に基づいて計算されます。円の中心は (0, 0) であるため、これらの点は円の中心から円周までの放射状ベクトルとして扱うこともできます。制御点は円に接する線上にあるため、これらの放射状ベクトルに対して直角になります。別のベクトルに対して直角のベクトルは、X 座標と Y 座標が入れ替えられ、そのうちの 1 つが負の値である元のベクトルです。

さまざまな角度で実行されたプログラムを次に示します。

角度が 180 度に設定された 3 つ目のスクリーンショットをよく見ると、ベジエ曲線が半円から著しく逸脱していることがわかりますが、角度が 90 度に設定された iOS 画面では、4 分の 1 の円にちょうど収まっているように見えます。

4 分の 1 の円を次のような向きにすると、2 つの制御点の座標を計算するのが非常に簡単です。

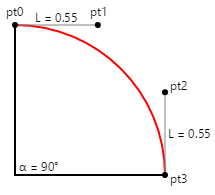
ベジエ曲線を使用した 4 分の 1 円弧の近似

円の半径が 100 の場合、L は覚えやすく、55 になります。

[Squaring the Circle] (円の正方形化) ページでは、円と正方形の間を変化する図形がアニメーション化されます。円は、SquaringTheCirclePage クラスの配列定義の最初の列に座標が表示される 4 つのベジエ曲線によって近似されます。

public class SquaringTheCirclePage : ContentPage
{
    SKPoint[,] points =
    {
        { new SKPoint(   0,  100), new SKPoint(     0,    125), new SKPoint() },
        { new SKPoint(  55,  100), new SKPoint( 62.5f,  62.5f), new SKPoint() },
        { new SKPoint( 100,   55), new SKPoint( 62.5f,  62.5f), new SKPoint() },
        { new SKPoint( 100,    0), new SKPoint(   125,      0), new SKPoint() },
        { new SKPoint( 100,  -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
        { new SKPoint(  55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
        { new SKPoint(   0, -100), new SKPoint(     0,   -125), new SKPoint() },
        { new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
        { new SKPoint(-100,  -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
        { new SKPoint(-100,    0), new SKPoint(  -125,      0), new SKPoint() },
        { new SKPoint(-100,   55), new SKPoint(-62.5f,  62.5f), new SKPoint() },
        { new SKPoint( -55,  100), new SKPoint(-62.5f,  62.5f), new SKPoint() },
        { new SKPoint(   0,  100), new SKPoint(     0,    125), new SKPoint() }
    };
    ...
}

2 列目には、面積が円の面積とほぼ同じ正方形を定義する 4 つのベジエ曲線の座標が含まれています。 (特定の円と "正確に一致する" 面積を持つ正方形を描画することは、円の正方形化において、長い間解決できていない幾何学的問題です)。ベジエ曲線を使用して正方形をレンダリングする場合、各曲線の 2 つの制御点は同じで、始点と終点の同一線上にあるため、ベジエ曲線は直線としてレンダリングされます。

配列の 3 列目は、アニメーションの補間値用です。このページでは 16 ミリ秒のタイマーを設定しているため、PaintSurface ハンドラーはその速度で呼び出されます。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    canvas.Translate(info.Width / 2, info.Height / 2);
    canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));

    // Interpolate
    TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
    float t = (float)(timeSpan.TotalSeconds % 3 / 3);   // 0 to 1 every 3 seconds
    t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2;     // 0 to 1 to 0 sinusoidally

    for (int i = 0; i < 13; i++)
    {
        points[i, 2] = new SKPoint(
            (1 - t) * points[i, 0].X + t * points[i, 1].X,
            (1 - t) * points[i, 0].Y + t * points[i, 1].Y);
    }

    // Create the path and draw it
    using (SKPath path = new SKPath())
    {
        path.MoveTo(points[0, 2]);

        for (int i = 1; i < 13; i += 3)
        {
            path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
        }
        path.Close();

        canvas.DrawPath(path, cyanFill);
        canvas.DrawPath(path, blueStroke);
    }
}

各点は、t の正弦振動値に基づいて補間されます。次に、補間された点を使用して、接続された 4 つのベジエ曲線を作成します。実行時のアニメーションを次に示します。

このようなアニメーションは、円弧と直線の両方としてレンダリングするのに十分なアルゴリズム的な柔軟性を持つ曲線がないと実現できません。

[Bezier Infinity] (ベジエ無限) ページでも、ベジエ曲線を利用して円弧を近似します。BezierInfinityPage クラスの PaintSurface ハンドラーを次に示します。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.MoveTo(0, 0);                                // Center
        path.CubicTo(  50,  -50,   95, -100,  150, -100); // To top of right loop
        path.CubicTo( 205, -100,  250,  -55,  250,    0); // To far right of right loop
        path.CubicTo( 250,   55,  205,  100,  150,  100); // To bottom of right loop
        path.CubicTo(  95,  100,   50,   50,    0,    0); // Back to center  
        path.CubicTo( -50,  -50,  -95, -100, -150, -100); // To top of left loop
        path.CubicTo(-205, -100, -250,  -55, -250,    0); // To far left of left loop
        path.CubicTo(-250,   55, -205,  100, -150,  100); // To bottom of left loop
        path.CubicTo( -95,  100,  -50,   50,    0,    0); // Back to center
        path.Close();

        SKRect pathBounds = path.Bounds;
        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
                                     info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

これらの座標をグラフ用紙にプロットして、それぞれの関連性を確認することをお勧めします。無限大記号は (0, 0) 点を中心とし、2 つのループは、中心が (–150, 0) と (150, 0) で、半径が 100 に設定されています。一連の CubicTo コマンドでは、-95 と –205 (これらの値は -150 プラスマイナス 55)、205 と 95 (150 プラスマイナス 55) の値を取る制御点の X 座標と、左右の辺の 250 と –250 が表示されます。唯一の例外は、無限大記号自体が中央で交差するときです。その場合、制御点の座標は 50 と –50 の組み合わせとなり、中心付近の曲線を直線化します。

無限大記号を次に示します。

「円弧を描画する 3 つの方法」の [Arc Infinity] (円弧無限) ページでレンダリングされる無限大記号よりも、中心に向かってやや滑らかになります。

2 次ベジエ曲線

2 次ベジエ曲線の制御点は 1 つだけであり、曲線は始点、制御点、終点の 3 点で定義されます。媒介変数表示方程式は、3 次ベジエ曲線によく似ていますが、最大指数は 2 であるため、曲線は 2 次多項式になります。

x(t) = (1 – t)²x₀ + 2t(1 – t)x₁ + t²x₂

y(t) = (1 – t)²y₀ + 2t(1 – t)y₁ + t²y₂

パスに 2 次ベジエ曲線を追加するには、別の x および y 座標を持つ QuadTo メソッドまたは QuadTo オーバーロードを使用します。

public void QuadTo (SKPoint point1, SKPoint point2)

public void QuadTo (Single x1, Single y1, Single x2, Single y2)

このメソッドは、現在の位置から point2 までの、制御点が point1 の曲線を追加します。

[Quadratic Curve] (2 次曲線) ページで 2 次ベジエ曲線を試すことができます。これは、接点が 3 箇所しかないことを除いて、[ベジエ曲線] ページとよく似ています。 QuadraticCurve.xaml.cs 分離コードファイルの PaintSurface ハンドラーを次に示します。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with quadratic Bezier
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.QuadTo(touchPoints[1].Center,
                    touchPoints[2].Center);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[1].Center.X,
                    touchPoints[1].Center.Y,
                    touchPoints[2].Center.X,
                    touchPoints[2].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

実行すると次のようになります。

点線は、始点と終点で曲線に接し、制御点で交わります。

2 次ベジエは、一般的な形状の曲線が必要ですが、制御点が 2 つよりも 1 つの方が好ましい場合に適しています。 2 次ベジエは他のどの曲線よりも効率的にレンダリングするため、楕円円弧をレンダリングするために Skia でも内部的に使用されています。

ただし、2 次ベジエ曲線の形状は楕円ではないため、楕円円弧を近似するためには複数の 2 次ベジエが必要になります。それよりも 2 次ベジエは放物線の線分です。

円錐ベジエ曲線

円錐ベジエ曲線 (有理 2 次ベジエ曲線とも呼ばれます) は、ベジエ曲線のファミリに比較的最近追加されました。 2 次ベジエ曲線と同様に、有理 2 次ベジエ曲線には始点、終点、1 つの制御点があります。しかし、有理 2 次ベジエ曲線には "重み" の値も必要になります。この媒介変数表示数式には比率が含まれるため、"有理" 2 次方程式と呼ばれます。

X と Y の媒介変数表示方程式は、分母が同じ比率です。 t の範囲を 0 から 1 で、重み値を w とする分母の方程式を次に示します。

d(t) = (1 – t)² + 2wt(1 – t) + t²

理論的には、有理 2 次方程式は、3 つの項それぞれに 1 ずつ、合計 3 つの個別の重み値を含むことができますが、これらは中項の 1 つの重み値のみに単純化することができます。

X 座標と Y 座標の媒介変数表示方程式は、2 次ベジエの媒介変数表示方程式に似ていますが、中項にも重み値が含まれており、式が分母で除算される点が異なります。

x(t) = ((1 – t)²x₀ + 2wt(1 – t)x₁ + t²x₂)) ÷ d(t)

y(t) = ((1 – t)²y₀ + 2wt(1 – t)y₁ + t²y₂)) ÷ d(t)

有理 2 次ベジエ曲線は、双曲線、放物線、楕円、円など、任意の円錐曲線の線分を正確に表すことができるため、"円錐曲線" とも呼ばれます。

パスに有理 2 次ベジエ曲線を追加するには、別の x および y 座標を持つ ConicTo メソッドまたは ConicTo オーバーロードを使用します。

public void ConicTo (SKPoint point1, SKPoint point2, Single weight)

public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)

最後の weight パラメーターに注目してください。

[Conic Curve] (円錐曲線) ページでは、これらの曲線を試すことができます。 ConicCurvePage クラスは、InteractivePage から派生したものです。 ConicCurvePage.xaml ファイルは、-2 から 2 の間の重み値を選択するために Slider のインスタンスを作成します。 ConicCurvePage.xaml.cs 分離コードファイルは、3 つの TouchPoint オブジェクトを作成し、PaintSurface ハンドラーは、結果として生成された制御点への接線を含む曲線をレンダリングします。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Draw path with conic curve
    using (SKPath path = new SKPath())
    {
        path.MoveTo(touchPoints[0].Center);
        path.ConicTo(touchPoints[1].Center,
                     touchPoints[2].Center,
                     (float)weightSlider.Value);

        canvas.DrawPath(path, strokePaint);
    }

    // Draw tangent lines
    canvas.DrawLine(touchPoints[0].Center.X,
                    touchPoints[0].Center.Y,
                    touchPoints[1].Center.X,
                    touchPoints[1].Center.Y, dottedStrokePaint);

    canvas.DrawLine(touchPoints[1].Center.X,
                    touchPoints[1].Center.Y,
                    touchPoints[2].Center.X,
                    touchPoints[2].Center.Y, dottedStrokePaint);

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

実行結果は次のようになります。

ご覧のように、重みが大きいと、制御点が曲線をより強く引き寄せていることがわかります。重みが 0 の場合、曲線は始点から終点までの直線になります。

理論上は、重みには負の値を設定でき、曲線は制御点から曲がって "離れます"。ただし、重みが -1 以下の場合、媒介変数表示方程式の分母が t の値に対して負になります。この理由から、ConicTo メソッドでは負の重みは無視される場合があります。 円錐曲線プログラムを使用すると、重みに負の値を設定できますが、実験でわかるように、重みが負の場合と 0 の場合では効果が同じで、直線がレンダリングされます。

ConicTo メソッドを使用して、半円 (含まない) まで円弧を描画する制御点と重みを導き出すのは非常に簡単です。次の図では、始点と終点の接線が制御点で交わっています。

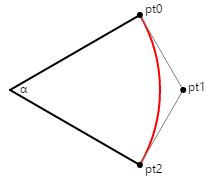
円弧の円錐弧レンダリング

三角法を使用して、円の中心から制御点までの距離を算出でき、円の半径を α の半分の角度の余弦で割ったものになります。始点と終点の間に円弧を描画するには、重みを同じ半分の角度の余弦に設定します。角度が 180 度の場合、接線は決して交わらず、重みは 0 になることに注意してください。しかし、180 度未満の角度では、この演算は正常に機能します。

[Conic Circular Arc] (円錐円弧) ページでこれを示します。 ConicCircularArc.xaml ファイルは、角度を選択するために Slider のインスタンスを作成します。 ConicCircularArc.xaml.cs 分離コードファイルの PaintSurface ハンドラーは、制御点と重みを計算します。

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    // Translate to center
    canvas.Translate(info.Width / 2, info.Height / 2);

    // Draw the circle
    float radius = Math.Min(info.Width, info.Height) / 4;
    canvas.DrawCircle(0, 0, radius, blackStroke);

    // Get the value of the Slider
    float angle = (float)angleSlider.Value;

    // Calculate sin and cosine for half that angle
    float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
    float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);

    // Find the points and weight
    SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
    SKPoint point1 = new SKPoint(0, radius / cos);
    SKPoint point2 = new SKPoint(radius * sin, radius * cos);
    float weight = cos;

    // Draw the points
    canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
    canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
    canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);

    // Draw the tangent lines
    canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
    canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);

    // Draw the conic
    using (SKPath path = new SKPath())
    {
        path.MoveTo(point0);
        path.ConicTo(point1, point2, weight);
        canvas.DrawPath(path, redStroke);
    }
}

ご覧のように、赤で表示されている ConicTo パスと、参照用に表示されている基となる円の間に視覚的な違いはありません。

しかし、角度を 180 度に設定すると、演算は失敗します。

理論上 (媒介変数表示方程式に基づく) では、同じ点を持つ ConicTo をもう一度呼び出すことで、重みが負の値でも円を完成させることができるので、この場合、ConicTo が負の重みをサポートしていないのは残念です。これにより、0 度と 180 度 (含まない) の間の角度に基づいて、2 つの ConicTo 曲線のみを含む円全体を作成できます。

SkiaSharp API

次の方法で共有

3 つの種類のベジエ曲線

3 次ベジエ曲線

円弧に対するベジエ曲線近似

2 次ベジエ曲線

円錐ベジエ曲線

その他のリソース

次の方法で共有

3 つの種類のベジエ曲線

3 次ベジエ曲線

円弧に対するベジエ曲線近似

2 次ベジエ曲線

円錐ベジエ曲線

関連リンク

その他のリソース