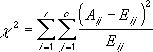WorksheetFunction.ChiSq_Test メソッド (Excel)
カイ 2 乗 (χ2) 検定を行います。
構文
式。ChiSq_Test (Arg1,Arg2)
式: WorksheetFunction オブジェクトを表す変数。
パラメーター
| 名前 | 必須 / オプション | データ型 | 説明 |
|---|---|---|---|
| Arg1 | 必須 | バリアント型 (Variant) | 期待値に対する検定の実測値が入力されているデータ範囲を指定します。 |
| Arg2 | 必須 | バリアント型 (Variant) | 期待値が入力されているデータ範囲を指定します。実測値と期待値では、行方向の値の合計と列方向の値の合計がそれぞれ等しくなっている必要があります。 |
戻り値
Double
注釈
ChiSq_Test は、統計と適切な自由度のカイ二乗 (χ2) 分布から値を返します。 χ2 テストを使用して、仮説の結果が実験によって検証されるかどうかを判断します。
actual_rangeとexpected_rangeに異なる数のデータ ポイントがある場合、 ChiSq_Test は #N/A エラー値を返します。
χ2 検定では、最初に次の数式を使用して χ2 統計量が計算されます。ここで、
- Aij = i 番目の行の実際の頻度、j 番目の列
- Eij = i 番目の行、j 番目の列の予想される頻度
- r = 数値または行
- c = 列の数
χ2 の低い値は、独立性の指標です。 数式からわかるように、χ2 は常に正または 0 で、i,j ごとに Aij = Eij の場合にのみ 0 です。
ChiSq_Test は、χ2 統計量の値が、独立を前提として偶然発生した可能性がある確率を、少なくとも前の数式で計算した値と同じ高さを返します。 この確率を計算する際に、 ChiSq_Test は自由度 df の適切な数の χ2 分布を使用します。
- r > 1 と c > 1 の場合、df = (r - 1)(c - 1)。
- r = 1 および c > 1 の場合、df = c - 1。
- r > 1 と c = 1 の場合、df = r - 1。
- r = c = 1 は許可されず、エラーが生成されます。
Eijのが小さすぎる場合は、ChiSq_Testの使用が最も適切です。 Eij の値がそれぞれ 5 以上の場合に使用するよう推奨する統計学者もいます。
サポートとフィードバック
Office VBA またはこの説明書に関するご質問やフィードバックがありますか? サポートの受け方およびフィードバックをお寄せいただく方法のガイダンスについては、Office VBA のサポートおよびフィードバックを参照してください。