hll() (集計*関数*)
適用対象: ✅Microsoft Fabric✅Azure データ エクスプローラー✅Azure Monitor✅Microsoft Sentinel
hll()関数は、値のセット内の一意の値の数を推定する方法です。 これを行うには、dcount関数を使用してデータグループのummarize演算子内の集計の中間結果を計算します。
基になるアルゴリズム* (HyperLogLog) と推定正確度について詳細を表示します。
Note
この関数は、summarize 演算子と組み合わせて使用します。
ヒント
- hll_merge関数を使用して、複数の
hll()関数の結果をマージします。 - dcount_hll関数を使用して、
hll()またはhll_merge関数の出力からの個別の値の数を計算します。
重要
hll()、hll_if()、およびhll_merge() の結果を格納し、後で取得できます。 たとえば、毎日の一意のユーザーの概要を作成し、それを使用して週単位のカウントを計算することができます。 ただし、これらの結果の正確なバイナリ表現は、時間の経過と同時に変化する可能性があります。 これらの関数が同一の入力に対して同じ結果を生成する保証はないため、それらに依存することはお勧めしません。
構文
hll(expr [, accuracy])
構文規則について詳しく知る。
パラメーター
| 件名 | タイプ | Required | 説明 |
|---|---|---|---|
| expr | string |
✔️ | 集計計算に使用される式。 |
| 精度 | int |
速度と精度のバランスを制御する値。 指定しない場合、既定値は 1 です。 サポートされている値については、「 Estimation accuracyを参照してください。 |
返品
グループ全体の expr の個別のカウントの中間結果を返します。
例
次の例では、hll()関数を使用して、StartTime列の各 10 分のタイム ビン内のDamageProperty列の一意の値の数を推定します。
StormEvents
| summarize hll(DamageProperty) by bin(StartTime,10m)
表示される結果テーブルには、最初の 10 行のみが含まれます。
| StartTime | hll_DamageProperty |
|---|---|
| 2007-01-01T00:20:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T01:00:00Z | [[1024,14],["7755241107725382121","-5665157283053373866","3803688792395291579","-1003235211361077779"],[]] |
| 2007-01-01T02:00:00Z | [[1024,14],["-1003235211361077779","-5665157283053373866","7755241107725382121"],[]] |
| 2007-01-01T02:20:00Z | [[1024,14],["7755241107725382121"],[]] |
| 2007-01-01T03:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T03:40:00Z | [[1024,14],["-5665157283053373866"],[]] |
| 2007-01-01T04:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T05:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T06:30:00Z | [[1024,14],["1589522558235929902"],[]] |
推定精度
この関数では、セット カーディナリティの確率的推定を行う HyperLogLog (HLL) アルゴリズム の異形が使用されます。 アルゴリズムには、メモリ サイズごとの精度と実行時間のバランスを取るために使用できる "ノブ" が用意されています。
| 精度 | エラー (%) | エントリ数 |
|---|---|---|
| 0 | 1.6 | 212 |
| 1 | 0.8 | 214 |
| 2 | 0.4 | 216 |
| 3 | 0.28 | 217 |
| 4 | 0.2 | 218 |
Note
"エントリ数" 列は、HLL 実装における 1 バイト カウンターの数です。
セット カーディナリティが十分に小さい場合、アルゴリズムには完璧なカウント (ゼロ エラー) を行うためのいくつかの条件が含まれています。
- 精度レベルが
1の場合は 1,000 個の値を返す - 精度レベルが
2の場合は 8,000 個の値を返す
誤り限界は確率的であり、理論限界ではありません。 値は、誤差分布の標準偏差 (シグマ) であり、推定量 の 99.7% は 3 x シグマ未満の相対エラーになります。
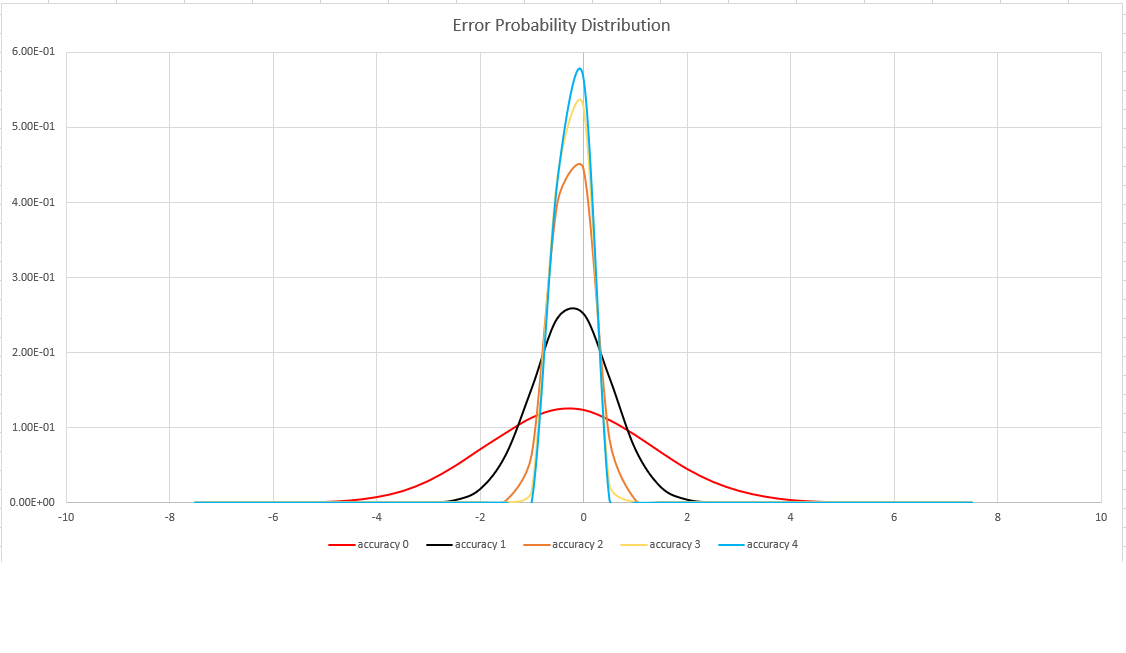
次の図は、サポートされているすべての精度設定の相対的な推定誤差の確率分布関数をパーセントで示したものです。