機械学習モデルの結果
この記事では、機械学習 (ML) モデルの混乱マトリックス、分類に関する問題、および正確性について説明します。 ML の予測結果の正確性について理解を深めることを目的としています。 対象者は、データサイエンスの知識やスキルを身につけたいエンジニア、アナリスト、管理者などです。
混乱マトリックス
一連の履歴データに関して、監督された ML の問題をトレーニングした後、トレーニング プロセスから取得したデータを使用してテストを行います。 このようにして、訓練されたモデルの予測値と実際の値を比較することができます。 混乱マトリックスには、分類の問題がどの程度成功しているか、どこで誤りが発生しているかを評価する手段を提供します。
たとえば、いくつかの身体的属性や行動的属性に基づいて、ペットが犬なのか猫なのかを予測するなどです。 30匹の犬と20匹の猫を含むテストのデータセットを使用している場合、混乱マトリックスは次の図のようになります。
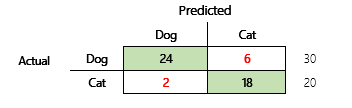
緑のセルの数値は、正しい予測を表します。 ご覧のように、モデルは猫の割合が高いことを予測していました。 モデルの全体的な精度は簡単に計算できます。 この場合は、42÷ 50 (0.84) になります。
混乱マトリックスの複数クラスの分類子
混乱マトリックスに関する議論のほとんどは、前述の例のように、2進分類子に焦点を置いています。 この場合は、特殊なケースとして、感度や呼び戻しといった他の指標を考えることができます。
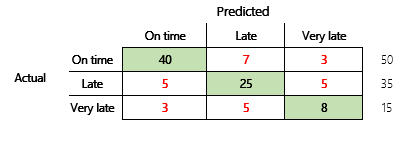
次に、3つの状態を持つファイナンス シナリオの分類に関する問題を検討します。 このモデルでは、顧客請求書が時間どおりに支払われるか、遅延しているか、または遅延しているかを予測します。 この場合、 テスト請求書 100 件のうち、50 件は定時払い、35 件は遅延、15 件は大幅に遅延しています。 この場合、モデルが次の図のような混乱マトリックスを生成する場合があります。
 ]
]
混乱マトリックスには、簡素な精度メトリックよりもはるかに多くの情報が提供されます。 ただし、わかりやすさを維持しています。 この混乱マトリックスでは、出力クラスのカウントが類似しているデータセットがあるかどうかを示します。 マルチクラスシナリオでは、前に示した顧客支払などのように、出力クラスが序数である場合に予測からどれだけ乖離しているかを示します。
モデルの精度
さまざまな精度基準を活用することで、モデルの品質を定量化できるという利点があります。
精度はわかりやすい指標であるため、特にデータ サイエンティストではないモデルのユーザーに対して、モデルを説明する際の出発点として適しています。 モデルの正確性を理解するためには、統計を把握することが必要となります。 混乱マトリックスが使用可能な場合は、モデルのパフォーマンスをさらに詳しく把握できます。
ただし、より詳細に理解するためには、正確さに関連するいくつかの問題に注意する必要があります。 メトリックの有用性は、問題のコンテキストによって異なります。 モデルのパフォーマンスに関してよくある質問は、「モデルのパフォーマンスはどうか」というものです。ただし、この質問の質問に対する回答は必ずしもシンプルではありません。 次の混乱マトリックスについて検討してください (モデル2)。
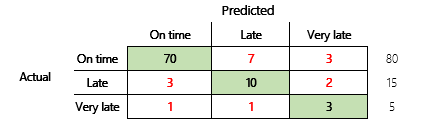
簡単な計算では、このモデルの精度 (70 + 10 + 3) ÷100 (0.83) が示されます。 表面的には、この結果は、精度 0.73 の以前のマルチ クラス モデル (モデル1) の結果よりも優れているようです。 ただし、それでも良いでしょうか。
この質問に対処するために、単純な推測が正確であることを考慮してください。 分類上の問題については、単純な推測は常に最も一般的なクラスを予測します。 モデル 1 では、この推測が 「時間通り」であり、0.50 の精度が得られることになります。 モデル 2 では、この推測が 「時間通り」であり、0.80 の精度が得られることになります。 モデル 1 は、0.73-0.50 = 0.23 によって単純な推測によって改善されているのに対し、モデル 2 は、0.83 による単純な予想 (0.80 = 0.03) を向上させているため、精度が低い場合でも、モデル 1 は優れたモデルと見なすことができます。 この計算から、モデルの品質を効果的に評価するには、精度の値よりも多くのコンテキストが必要になることがわかります。
もうひとつ注目すべき点があります。 医療検査で病気を発見するシナリオを考えてみましょう。 この問題は、正の結果が患者に病気があることを示す二項分類の問題です。 このシナリオでは、次のエラーの影響について考慮する必要があります。
- 偽陽性: 検査では患者に病気があると出ても、実際には病気ではない場合
- 偽陽性: 検査では患者に病気があると出ても、実際には病気ではない場合
明らかに、どちらのタイプのエラーも望ましいものではありませんが、どちらが悪いのでしょうか? これは状況によります。 迅速な治療が必要な生命に関わる病気の場合は、偽陰性の最小化 (可能な場合は別途追加検査を行う) が優先されます。 それ以外の重要度の低い状況では、モデル作成者は偽陽性を最小限に抑えることができるでしょう。 いずれにしても、モデルの品質を効果的に判断するにあたっては、精度の指標よりも多くの情報を持っている必要があるというのが、合理的な結論です。
推奨
精度は、統計学に精通していないドメイン専門家とコミュニケーションをとるための重要なツールです。 ただし、情報を有用にするために、精度の値と一緒に追加のコンテキストを提供することが重要です。
支払予測シナリオについては、異なる支払動作の係数を含む ML モデルのターゲットを設定できます。 目標は、誤った回答の数を少なくとも 50 パーセント減少させることによって、単純な推測でモデルを改善することです。 言い換えると、単純な推測と100% の精度を分割するターゲット精度が必要です。
以下の表では、この記事の混乱マトリックスについて、この原則をまとめています。
| モデル | 単純推測 | ターゲット | モデルの精度 | 目標が満たしているかどうか |
|---|---|---|---|---|
| モデル 1 | 0.50 | 0.75 | 0.73 | ほぼ。 このモデルは、推測に応じて大幅に改善されます。 |
| モデル 2 | 0.80 | 0.90 | 0.83 | No. 改善が必要です。 |
分類 F1 の精度
この記事の最後の考察では、より高度な測定を行う分類 ML パフォーマンスである F1 精度について解説します。
F1 精度を定義する前に、精度とリコールという 2 つの追加指標を導入する必要があります。 精度は、陽性として指定された予測の合計数のうち、正しく割り当てられている数を示します。 この指標は、陽性の予測値としても知られています。 リコールとは、正しく予測された実際の陽性例の総数です。 この指標は感度としても知られています。
前の図の混乱マトリックスでは、これらメトリックは次のように計算されます。
- 精度 = TP ÷ (TP + FP)
- リコール = TP ÷ (TP + FN)
F1 のメジャーは、精度とリコールを結合します。 この結果は、2 つの値の調和平均になります。 計算処理は次のように行われます。
- F1 = 2 × (精度 × リコール) ÷ (精度 + リコール)
具体的な例を以下に示します。 この記事では、動物の種類を予測モデルの例を示しました。 ここでも同じ図を使用します。
ここでは、"犬" を正の答えとして使用した場合の結果を示します。
- 精度 = 24 ÷ (24 + 2) = 0.9231
- リコール = 24 ÷ (24 + 6) = 0.8
- F1 = 2 × (0.9231 × 0.8) ÷ (0.9231 + 0.8) = 0.8572
ご覧のように、F1の値は精度とリコールの値の間にあります。
F1 の精度を理解するのは簡単ではありませんが、基本的な精度の数字には、微妙な精度が追加されます。 また、次の説明に示すように、不安定なデータセットに対応することもできます。
この記事のモデルの精度セクションでは、次の 2 つの混乱マトリックスを比較しています。 1 つ目のモデルでは精度が低かったにもかかわらず、定時払いの既定の推測よりも改善が見られたため、より有用なモデルと判断されました。


この 2 つのモデルを F1 スコアで比較してみましょう。 F1 スコアは、各状態の精度とリコールを考慮し、F1 マクロ計算で状態間の F1 スコアを平均化し、全体的な F1 スコアを決定します。 他にも F1 の変種はありますが、3 つの状態すべてに平等に考慮されていることを考えると、マクロ版を検討する価値がありそうです。
計算を簡単にするにあたり、実際の値と予測値を一致させるサンプルの配列を構築しました。 これらの配列は、Python の sklearn のメトリクスライブラリを使って計算していました。 結果を次に示します。
| モデル | 単純推測 | 正確性 | F1 マクロ |
|---|---|---|---|
| モデル 1 | 0.5 | 0.73 | 0.67 |
| モデル 2 | 0.80 | 0.83 | 0.66 |
この計算方法の詳細については、モデル 1 の sklearn.metrics の分類レポートを参照してください。 3 つの状態 "時間通り"、"遅延"、"大きく遅延" は、それぞれ 1、2、3 というラベルの行で表されています。 マクロ平均は、"f1-スコア" 列の平均値になります。
| 精度 | リコール | f1-スコア | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
これらの結果が示すように、2 つのモデルの F1 マクロ精度スコアはほぼ同じです。 このような場合あるいはその他多くのケースでは、F1 の精度はモデルの能力を示すより良い指標となります。 精度については、結果の解釈では、モデルで考慮すべき最も重要なことを理解する必要があります。
