量子コンピューティングにおける量子ビット
ビットが、従来のコンピューティングにおける情報の基本的オブジェクトであるのと同様に、"量子ビット" (qubit) は、量子コンピューティングにおける情報の基本的オブジェクトです。 この対応を理解するために、この記事では、単一量子ビットという最も単純な例を見ていきます。
量子ビットの表現
ビット (2 進数) の値は、$0$ または $1$ のいずれかの可能性がありますが、量子ビットの値は、$0$、$1$、または $0$ と $1$ の量子重ね合わせのいずれかである可能性があります。
単一量子ビットの状態は、単位ノルムの 2 次元列ベクトルで記述できます。つまり、そのエントリの大きさの二乗の合計が $1$ になる必要があります。 このベクトルは、量子状態ベクトルと呼ばれ、1 つのビットがバイナリ変数の状態を記述するのに必要なすべての情報を保持するのと同様に、単一量子ビットの量子系を記述するのに必要なすべての情報が保持されます。 量子コンピューティングにおけるベクトルと行列の基本については、「 ベクトルと行列を参照してください。
ノルム $1$ を含む実数または複素数の 2 次元列ベクトルはすべて、量子ビットによって保持されている可能性のある量子状態を表します。 したがって $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ は、$\alpha$ と $\beta$ が $|\alpha|^2 + |\beta|^2 = 1$ を満たす複素数である場合は量子状態を表します。 次、量子ビットを表現する有効な量子状態ベクトルの例の一部を示します。
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}、\begin{bmatrix} 0 \\ 1 \end{bmatrix}、\begin{bmatrix}\frac{{1}{\sqrt{2}}\\\frac{{1}{\sqrt{2}}\end{bmatrix}、\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{{-1}{\sqrt{2}}\end{bmatrix}、\text{}\begin{bmatrix}\frac{1}{\sqrt{{2}}\\\frac{i}{\sqrt{2}}\end{bmatrix}$$
量子状態ベクトルの $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ と $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ は、特別な役割を担います。 これらの 2 つのベクトルは、量子ビットの状態を記述するベクトル空間の基礎となります。 これは、どのような量子状態ベクトルであっても、これらの基礎ベクトルの合計として記述できることを意味します。 具体的には、ベクトル $\begin{bmatrix} x \\ y \end{bmatrix}$ は、$x \begin{bmatrix} 1 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \end{bmatrix}$ として記述できます。 これらのベクトルの回転はすべて、量子ビットの完全に有効な基底として機能しますが、この特定のものは "計算上の基底" と呼んで選択されます。
これらの 2 つの量子状態は、古典的なビットの 2 つの状態 (すなわち $0$ と $1$) に対応するために使用されます。 選択する標準的な規則は
$$0\equiv\begin{bmatrix} 1 \\ 0 \end{bmatrix}、\qquad 1 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix}$$
ですが、逆の選択も同様にすることができます。 このため、無限の数のありえる単一量子ビットの量子状態ベクトルのうち、2 つだけが古典的なビットの状態に対応しており、その他すべての量子状態はそうではありません。
量子ビットの測定
量子ビットの表現方法について説明したので、"測定" の概念について確認することにより、これらの状態が何を表すかについて一定の知識を得ることができます。 測定は、量子ビットを "見る" ことの非公式の考え方に対応します。測定では、量子の状態が直ちに 2 つの古典的な状態 $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ または $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ のいずれかに折りたたまれます。 量子状態ベクトル $\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ によって指定された量子ビットが測定されると、確率が $|\alpha|^2$ の結果 $0$ と、確率が $|\beta|^2$ の結果 $1$ が得られます。 結果 $0$ では、量子ビットの新しい状態は $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ で、結果 $1$ での状態は $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ です。 正規化の条件 $|\alpha|^2 + |\beta|^2 = 1$ のために、これらの確率は合計で $1$ になることに注意してください。
測定の特性は、量子状態ベクトルの全体的符号は関連性がないことも意味します。 ベクトルの符号を反転することは、$\alpha\rightarrow -\alpha$および $\beta\rightarrow -\beta$ と同等です。 $0$ と $1$ を測定する確率は、項の大きさの二乗によって決まるため、そのような記号を挿入しても、いかなる確率も変化しません。 そのような位相は一般に、"グローバル位相" と呼ばれ、より一般的には、ただ $\pm 1$ とするのではなく、$e^{i \phi}$ の形式にできます。
測定の最後の重要な特性は、測定によって必ずしもすべての量子状態ベクトルが破損するとは限らないということです。 古典的な状態 $0$ に対応する状態が $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ の量子ビットで開始した場合、この状態を測定すると常に結果 $0$ が生成されて、量子状態は変更されないままになります。 この意味では、古典的なビット (たとえば $\begin{bmatrix}1 \\ 0 \end{bmatrix}$ または $\begin{bmatrix}0 \\ 1 \end{bmatrix}$ のいずれかである量子ビット) だけがある場合は、測定によってシステムが破損することはありません。 これは、古典的コンピューターでは可能なのとまったく同様に、古典的データをレプリケートして量子コンピューターで操作できることを意味します。 ただし、両方の状態の情報を一度に格納する機能は、量子コンピューティングを、古典的な方法で可能なことの先へと向上させ、さらに、量子コンピューターから量子データを無差別にコピーする機能を奪うものです。量子複製不可能定理に関するページも参照してください。
Bloch 球を使用した量子ビットと変換の視覚化
量子ビットは、"ブロッホ球" の表現を使用して、$3$D の図で示すこともできます。 ブロッホ球は、単一量子ビットの量子状態 (これは 2 次元の複合ベクトルです) を、実際の値を持つ 3 次元のベクトルとして記述する方法となっています。 これが重要なのは、単一量子ビットの状態を視覚化し、その結果、複数量子ビットの状態を理解するうえでそれが非常に貴重である場合がある (残念なことにブロッホ球表現が壊れている場合) という根拠を明らかにできるためです。 ブロッホ球は以下のように視覚化できます。
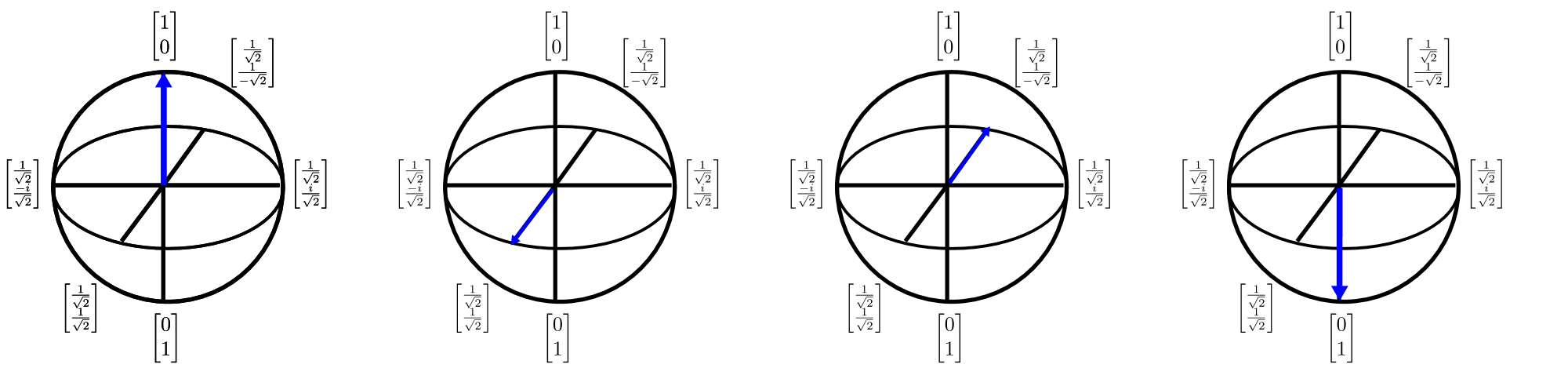
この図の矢印は、量子状態ベクトルが指している方向を示しています。矢印のそれぞれの変換は、基本軸の 1 つを中心とした回転と考えることができます。 量子計算を一連の回転として考えることは説得力のある直感的洞察ですが、この洞察を利用してアルゴリズムを設計し、記述することは難易度が高い作業です。 Q# は、そのような回転を記述するための言語を提供することで、この問題を軽減します。
単一量子ビット演算
量子コンピューターでは、量子状態ベクトルのすべての回転をエミュレートできる、一連の汎用量子ゲートを適用することで、データを処理します。 この普遍性の概念は、従来の (たとえば古典的) コンピューティングの普遍性の概念に似ています。これは、長さに限りがある回路を使用して入力ビットのすべての変換を実行できる場合、ゲート セットは普遍的であると見なされることを意味します。 量子コンピューティングでは、量子ビットに対して実行することが許されている有効な変換は、ユニタリ変換と測定です。 量子変換を反転させる必要があるため、"随伴演算" すなわち複素共役転置は、量子コンピューティングにとって非常に重要です。
単一量子ビット演算または単一量子ビット量子ゲートは、クリフォード ゲートと非クリフォード ゲートの 2 つのカテゴリに分類できます。 非クリフォード ゲートは、 $T$ ゲート ( $\pi/8$ ゲートとも呼ばれます) のみで構成されます。
$$ T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\end{bmatrix}。 $$
Q#に既定で含まれる単一量子ビットのクリフォード ゲートの標準セットには、次のものが含まれます。
$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 &1 \\ 1& 0 \end{bmatrix}= HT^4H, $$
$$ Y =\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&0\\ 0&-1 \end{bmatrix}=T^4。 $$
ここで演算 $X$、$Y$、$Z$ は、特に頻繁に使用されるもので、作成者である Wolfgang Pauli にちなみ、"パウリ演算子" と命名されています。 非クリフォード ゲート ($T$ ゲート) と共に、これらの演算は、単一量子ビットに対して任意のユニタリ変換の近似値を求めるように構成できます。
前記のものでは、スタックの論理レベル (この論理レベルは量子アルゴリズムのレベルだと考えてください) での演算を記述するために、最も一般的なプリミティブ ゲートを構成していますが、多くの場合、たとえば関数の記述レベルに近い演算のように、アルゴリズム レベルでの基本的演算の数を減らすことを検討すると便利です。 幸い Q# には、より高レベルのユニタリを実装するために使用できるメソッドも用意されています。今度はこれらを使用すれば、すべてをクリフォード ゲートと $T$ ゲートに明示的に分解することなく、高レベルのアルゴリズムを実装できます。
そのような最も単純なプリミティブは、単一量子ビットの回転です。 一般に、$R_x$、$R_y$、$R_z$ という 3 種類の単一量子ビットの回転が検討されます。 たとえば、回転 $R_x(\theta)$ のアクションを視覚化するには、右の親指をブロッホ球の $x$ 軸の方向に沿って指して、そのベクトルを手で、$\theta/2$ ラジアンの角度で回転させます。 この混乱させる要素の $2$ は、直交ベクトルがブロッホ球に記入されたときに $180^\circ$ 離れていても、実際には幾何学的に $90^\circ$ 度離れているという事実に起因します。 対応するユニタリ行列は次のとおりです。
\begin{align*}&R_z(\theta) = e^{-i\theta Z/2}=\begin{bmatrix} e^{-i\theta/2}& 0\\ 0& e^{i\theta/2}\end{bmatrix}, \\&R_x(\theta) = e^{-i\theta X/2}= HR_z(\theta)H =\begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2)\\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix}, \\&R_y(\theta) = e^{-i\theta Y/2}= SHR_z(\theta)HS^\dagger=\begin{bmatrix} \cos(\theta/2) & -\sin(\theta/2)\\ \sin(\theta/2) & \cos(\theta/2) \end{bmatrix}。 \end{align*}
3 種類の回転を一緒に組み合わせて 3 次元で任意の回転を実行できるのと同様に、ブロッホ球表現からは、すべてのユニタリ配列を一連の 3 種類の回転として記述できることもわかります。 具体的には、すべてのユニタリ行列 $U$ に対して、$U= e^{i\alpha} R_x(\beta)R_z(\gamma)R_x(\delta)$ であるような $\alpha,\beta,\gamma,\delta$ が存在します。 したがってこれは、$\theta$ は任意の値を取ることができるため不連続なセットではありませんが、$R_z(\theta)$ と $H$ でもユニバーサル ゲート セットが形成されます。 この理由で、また、量子シミュレーションにおけるアプリケーションのために、そのような連続的ゲートは、量子計算、特に量子アルゴリズムの設計レベルで不可欠です。 フォールト トレラントなハードウェア実装を実現するため、これらは最終的には、これらの回転を厳密に近似する別個のゲート シーケンスにコンパイルされます。