クォータニオンでスキンアニメーション
2010/09/17 追記: XNA Game Studio 4.0用のサンプルをhttp://higeneko.net/hinikeni/sample/xna40/QuatSkinningSample.zipにアップしました。詳細は「サンプルコードをXNA 4.0向けに更新」を見てください。
2009/06/25 追記: XNA GS 3.1用のサンプルを http://higeneko.net/hinikeni/sample/xna31/QuatSkinningSample.zipにアップしました。
クォータニオンでボーン処理、その4:その実装
クォータニオンを使ってのボーン処理の記事も4回目になりました。今回はいよいよい実際にクォータニオンを使ったスキニングアニメーションの実装方法を紹介します。
XNA Game Studio 3.0で動作するサンプルを用意しました。基本的にSkinned Modelサンプルと同じ使い方です。
http://higeneko.net/hinikeni/sample/QuatSkinningSample.zip
変更部分はもちろん、オリジナルのコードのコメントも翻訳しているので、理解する手助けになると思います。
クォータニオンでボーン処理するためにはオリジナルサンプルに以下の変更を加えます。
- QuatTransformの実装
- AnimationPlayerの変更
- シェーダーの変更
QuatTransformの実装
まずはMatrix構造体の代わりに回転部分をクォータニオン、平行移動部分をVector3で表したQuatTransform構造体を作ります。この構造体は回転と平行移動を結合した行列と同じ振る舞いをします。これで使用するメモリがMatrixの半分以下になります。
public struct QuatTransform
{
public Quaternion Rotation; // 回転
public Vector3 Translation; // 平行移動
}
次に、行列からQuatTransformへの変換コードを実装します。これは単純にMatrix.Decomposeを使って回転部分と平行移動部分に分割した結果をそのまま使うだけです。サンプルコードではこれ以外にもスケール部分に1以外の値が使われていないかのチェックをしてありますが、ここでは割愛します。
public static QuatTransform CreateFromMatrix( Matrix matrix )
{
// 行列の分解
Quaternion rotation;
Vector3 translation, scale;
matrix.Decompose( out scale, out rotation, out translation );
return new QuatTransform( rotation, translation );
}
最後に、QuatTransformの結合の実装をします。ここでは演算オーバーロードを使っていますが、好みに合わせてメソッド化するといいでしょう。QuatTransform内の回転と平行移動の評価順は回転した後に平行移動となっているので、以下のコードのようにして結合します。
public static QuatTransform operator *(QuatTransform value1, QuatTransform value2)
{
// 平行移動の算出
Vector3 newTranslation;
Vector3.Transform(ref value1.Translation, ref value2.Rotation,
out newTranslation);
newTranslation.X += value2.Translation.X;
newTranslation.Y += value2.Translation.Y;
newTranslation.Z += value2.Translation.Z;
// 回転部分の結合
QuatTransform result;
Quaternion.Concatenate(ref value1.Rotation, ref value2.Rotation,
out result.Rotation);
result.Translation = newTranslation;
return result;
}
これでCPU側でスキンアニメーションに必要な最低限の機能が実装できました。後は、コンテントプロセッサ内やアニメーションプレイヤーでMatrixを指定している場所をQuatTransformに置き換えていきます。
AnimationPlayerの変更
オリジナルのAnimationPlayerのGetSkinTransformメソッドはMatrixの配列を返していました。それに倣ってQuatTransformの配列を返すようにしたいのですが、QuatTransform配列そのままでは定数レジスタに設定することができません。
そこで、定数レジスタに設定しやすいように、回転部分をQuaternion配列で返すGetSkinRotations, 平行移動部分をVector3配列で返すGetSkinTranslationsに置き換えます。
それぞれの配列にはUpdateSkinTransformsメソッド内で回転部分、平行移動部分の情報を分割して格納しています。
public void UpdateSkinTransforms()
{
for (int bone = 0; bone < skinRotations.Length; bone++)
{
QuatTransform xform =
skinningDataValue.InverseBindPose[bone] * worldTransforms[bone];
skinRotations[bone] = xform.Rotation;
skinTranslations[bone] = xform.Translation;
}
}
QuatTransformが格納できる情報は回転と平行移動だけです。オリジナルのサンプルではMatrixを指定できるようになっていたので、スケールが入ったMatrixをワールド行列として指定することができました。ですが、QuatTransformではスケールが入った行列を扱うことができません。
また、実際のゲームの場合、同じアニメーションを複数回、違ったワールド座標を指定して描画することが良くあります。例えば、複数のキャラクターが街中を歩き回っている場合、キャラクターごとにアニメーションを更新するのは計算コストが掛かるので、複数のキャラクターで同じアニメーションを共有して、ワールド座標だけを変えて描画することで計算コストを抑えることができます。
以上の理由から、このサンプルではワールド座標とのAnimationPlayer内ではなく、シェーダー内で行うようにしました。
シェーダーの変更
シェーダーの変更点ですが、まず今まではfloat4x4の配列だったものを、回転部分と平行移動部分の二つに分けた配列を用意します。これで、定数レジスタの使用量はオリジナルのサンプルの半分になるので、最大117ボーンが使えます。以前の記事で118と書きましたが、ワールド座標情報を追加したことでひとつ減って117になりました。
// 最大ボーン数
// この数値を変えた時にはSkinnedModelProcessorの
// MaxBonesも変えることを忘れないように
#define MaxBones 117
float4 BoneRotations[MaxBones]; // ボーンの回転部分
float3 BoneTranslations[MaxBones]; // ボーンの平行移動部分
後は行列と同じようにBoneRotations、BoneTranslationsをそれぞれそブレンディングして、行列に変換すれば動きそうに思えますが、実はそのままでは動きません。前述のように、QuatTransformは言い換えれば、回転行列と移動行列をつなぎ合わせたものだということに気をつけないといけません。
通常の行列のブレンディングは以下の式で表されます。Lerpは線形補間関数、Mは行列、tはブレンド率を表します。
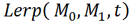
これをクォータニオンを使ったブレンディングの場合、行列Mは回転部分のRと平行移動部分のTで表されるので、以下の式になります。
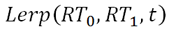 もし、回転部分と平行移動部分を別々にブレンディングすると以下のような式になります。
もし、回転部分と平行移動部分を別々にブレンディングすると以下のような式になります。
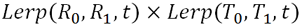 この式の意味は 「二つの回転を補間した回転の後に二つの平行移動を補間した分移動する」 という、まったく違う意味になってしまいます。
この式の意味は 「二つの回転を補間した回転の後に二つの平行移動を補間した分移動する」 という、まったく違う意味になってしまいます。
そこでシェーダー内でQuatTransformを行列に変換してからブレンディングする必要があります。QuatTransformから行列への変換コードは以下のようになります。
// クォータニオンと平行移動から行列に変換する
// スキニングに使用する場合、単純にこのメソッドを4回呼ぶのが理想的だが
// SM2.0だと一時レジスタ(12個)を超えてしまうので、そのままでは使えない
float4x4 CreateTransformFromQuaternionTransform( float4 quaternion, float3 translation )
{
float4 q = quaternion;
float ww = q.w * q.w - 0.5f;
float3 v00 = float3( ww , q.x * q.y, q.x * q.z );
float3 v01 = float3( q.x * q.x, q.w * q.z,-q.w * q.y );
float3 v10 = float3( q.x * q.y, ww, q.y * q.z );
float3 v11 = float3( q.w * q.z,-q.y * q.y, q.w * q.x );
float3 v20 = float3( q.x * q.z, q.y * q.z, ww );
float3 v21 = float3( q.w * q.y,-q.w * q.x, q.z * q.z );
return float4x4(
2.0f * ( v00 + v01 ), 0,
2.0f * ( v10 + v11 ), 0,
2.0f * ( v20 + v21 ), 0,
translation, 1
);
}
このメソッドはひとつのQuatTransformを変換するのには便利ですが、最大4つのボーンブレンディングが必要になるスキンアニメーションで使うと、SM2.0では一時レジスタの数が足りないというコンパイルエラーがでてしまいます。これは、シェーダーコンパイラーの最適化は複雑なスカラー計算をシェーダーが得意なベクトル計算へ���変換できないことが’原因です。
そこで、ひとつひとつのボーンを行列に変換してブレンディングするのではなく、4つのボーンをまとめて行列に変化する形式に書き直すことで、ベクトル計算の利点を活用するようにします。
// 4つクォータニオンと平行移動から行列に変換する
// SM2.0の一時レジスタ(12個)数制限を回避するために、一時レジスタの使用量を抑えるように
// 書き換えたもの
float4x4 CreateTransformFromQuaternionTransforms(
float4 q1, float3 t1,
float4 q2, float3 t2,
float4 q3, float3 t3,
float4 q4, float3 t4,
float4 weights )
{
float ww = q1.w * q1.w - 0.5f;
float3 row10 = float3( ww , q1.x * q1.y, q1.x * q1.z ) +
float3( q1.x * q1.x, q1.w * q1.z,-q1.w * q1.y );
float3 row11 = float3( q1.x * q1.y, ww, q1.y * q1.z ) +
float3(-q1.w * q1.z, q1.y * q1.y, q1.w * q1.x );
float3 row12 = float3( q1.x * q1.z, q1.y * q1.z, ww ) +
float3( q1.w * q1.y,-q1.w * q1.x, q1.z * q1.z );
ww = q2.w * q2.w - 0.5f;
float3 row20 = float3( ww, q2.x * q2.y, q2.x * q2.z ) +
float3( q2.x * q2.x, q2.w * q2.z,-q2.w * q2.y );
float3 row21 = float3( q2.x * q2.y, ww, q2.y * q2.z ) +
float3(-q2.w * q2.z, q2.y * q2.y, q2.w * q2.x );
float3 row22 = float3( q2.x * q2.z, q2.y * q2.z, ww ) +
float3( q2.w * q2.y,-q2.w * q2.x, q2.z * q2.z );
ww = q3.w * q3.w - 0.5f;
float3 row30 = float3( ww, q3.x * q3.y, q3.x * q3.z ) +
float3( q3.x * q3.x, q3.w * q3.z,-q3.w * q3.y );
float3 row31 = float3( q3.x * q3.y, ww, q3.y * q3.z ) +
float3(-q3.w * q3.z, q3.y * q3.y, q3.w * q3.x );
float3 row32 = float3( q3.x * q3.z, q3.y * q3.z, ww ) +
float3( q3.w * q3.y,-q3.w * q3.x, q3.z * q3.z );
ww = q4.w * q4.w - 0.5f;
float3 row40 = float3( ww, q4.x * q4.y, q4.x * q4.z ) +
float3( q4.x * q4.x, q4.w * q4.z,-q4.w * q4.y );
float3 row41 = float3( q4.x * q4.y, ww, q4.y * q4.z ) +
float3(-q4.w * q4.z, q4.y * q4.y, q4.w * q4.x );
float3 row42 = float3( q4.x * q4.z, q4.y * q4.z, ww ) +
float3( q4.w * q4.y,-q4.w * q4.x, q4.z * q4.z );
float4 w2 = 2.0f * weights;
return float4x4(
row10 * w2.x + row20 * w2.y + row30 * w2.z + row40 * w2.w, 0,
row11 * w2.x + row21 * w2.y + row31 * w2.z + row41 * w2.w, 0,
row12 * w2.x + row22 * w2.y + row32 * w2.z + row42 * w2.w, 0,
t1 * weights.x + t2 * weights.y + t3 * weights.z + t4 * weights.w, 1
);
}
コード量は多くなりますが、単純に前述のメソッドを4回コピーしたものになっています。また、処理速度的にもオイラー角を使った場合だとSin、Cosといった三角関数を使う必要がありますが、クォータニオンの場合は単純な積和演算で済むので速度的にも優位です。
これで、オリジナルのシェーダーコードのskinTransformが計算できました。最後に、ワールド座標変換行列と結合することで、頂点変換、ライティング計算用の法線変換にも使えるskinTransformになります。
// スキン変換行列の取得
float4x4 skinTransform = CreateTransformFromQuaternionTransforms(
BoneRotations[input.BoneIndices.x], BoneTranslations[input.BoneIndices.x],
BoneRotations[input.BoneIndices.y], BoneTranslations[input.BoneIndices.y],
BoneRotations[input.BoneIndices.z], BoneTranslations[input.BoneIndices.z],
BoneRotations[input.BoneIndices.w], BoneTranslations[input.BoneIndices.w],
input.BoneWeights );
skinTransform = mul( skinTransform, World );
// 頂点変換
float4 position = mul(input.Position, skinTransform);
output.Position = mul(mul(position, View), Projection);
// 法線変換
float3 normal = normalize( mul( input.Normal, skinTransform));
// 他の処理
定数レジスタ使用数が半分になった
オリジナルのサンプルではひとつのボーンに4つの定数レジスタが必要でしたが、クォータニオンと平行移動の組み合わせにすることで、使用する定数レジスタの数は2つになり、最大ボーン数が117個になりました。また、ボーン数を117個以下にして余った定数レジスタを他の用途に使うこともできるようになりました。
CPU側の使用するメモリが半分以下になるのはもちろん、メモリアクセス数が半減することで速度的にも有利になります。
ただし、以下の点に気をつける必要があります。
- スケールを持つポーンアニメーションには対応していない
通常、スキンアニメーションにはスケール情報は使わないので殆どの場合は問題はありませんが、どうしてもスケール情報を追加したい場合、そのスケール値の条件によって2つのオプションがあります。
ひとつは、追加するスケール情報が一意、つまりスケールのx,y,zの値が同じ場合のみのスケールに対応するのであれば、QuatTransformにfloat形のスケールを追加し、QuatTransformの結合部分、シェーダー内の行列変換部分を書き換えるだけで比較的容易に実現できます。
追加するスケール値が一意でない場合、安直にQuatTransformにVector3のスケールを追加してしまうと、必要になる定数レジスタが3つになってしまい、QuatTransformのメモリ消費量の少なさという利点を失ってしまいます。ですから、こういったスケール値を追加したい場合は、QuatTransformよりも単なる行列を使用した方が良いでしょう。
クォータニオンを使おう
今回のサンプルの目的のひとつは使えるボーン数を増やすことですが、もうひとつの目的はクォータニオンの有効利用法のひとつを紹介することでした。
アニメーションデータが日増しに多くなっている昨今、殆どのゲームではクォータニオンを使ってアニメーションデータの圧縮をしています。また、今まで紹介してきたように自由な回転を扱うケースでもクォータニオンは使われています。
これを機にクォータニオンをあなたのゲームでも使ってみてはどうでしょうか?
もっと骨が欲しい
今回のサンプルではボーン数が最大117まで使えるようになりましたが、次回からは使えるボーン数が256個になる手法を紹介します。
Comments
Anonymous
May 05, 2009
PingBack from http://microsoft-sharepoint.simplynetdev.com/%e3%82%af%e3%82%a9%e3%83%bc%e3%82%bf%e3%83%8b%e3%82%aa%e3%83%b3%e3%81%a7%e3%82%b9%e3%82%ad%e3%83%b3%e3%82%a2%e3%83%8b%e3%83%a1%e3%83%bc%e3%82%b7%e3%83%a7%e3%83%b3/Anonymous
May 05, 2009
Lerpを使っての処理で 90度以上の差があるクォータニオンの補間は大丈夫でしょうか? 関節が膨らんだり、破綻したりしないのでしょうか?Anonymous
May 05, 2009
Lerpと言うのが、この記事にでてくるLerpのことであれば、行列へ変換後のLerpなので大きな角度間の補間では問題があります。 もし、Quaternion.Lerpのことを指すのであれば、いかなる角度間でも問題なく補間できます。また、XNAフレームワーク内のQuaternion.Lerpでは補間後に正規化をしているので常に純粋な回転状態を保ち、歪んだりすることもありません。Anonymous
May 07, 2009
頂点テクスチャでスキンアニメーション、その2:頂点テクスチャでスキンアニメーション 今回は頂点テクスチャを使ったスキンアニメーションの実装方法を紹介します。 XNA Game Studio 3.0で動作するサンプルを用意しました。基本的にAnonymous
May 10, 2009
vFetchでスキンアニメーション 、その3: vFetchでスキンアニメーション スキンアニメーションで使えるボーン数を増やそうシリーズの記事も10回目となる今回で終わりです。今回はvFetchを使ったスキンアニメーションの実装例を紹介します。