Oltre la disponibilità del Gruppo di disponibilità del database

[アーティクル]
11/17/2011

Articolo originale pubblicato venerdì 16 settembre 2011

Definizioni

Come è noto, nell'ambito di Microsoft Exchange l'acronimo DAG indica il “Database Availability Group”, ovvero il Gruppo di disponibilità del database.

Database poiché in un server Cassette postali di Exchange 2010 a disponibilità elevata il database, non il server, è l'unità di disponibilità e viene sottoposto a failover o passaggio tra più server in Gruppo di disponibilità del database. Questo concetto è noto come mobilità del database.

Gruppo poiché l'ambito di disponibilità viene determinato dai server Cassette postali in un Gruppo di disponibilità del database combinati in un cluster di failover e che lavorano insieme come gruppo.

Disponibilità questo termine sembra essere il meno ovvio e il meno chiaro ed entrambi gli altri termini vi fanno riferimento. Ironicamente, dispone di una chiara definizione matematica e riveste un ruolo importante nella comprensione dei principi complessivi di progettazione di Exchange.

Wikipedia indica per “disponibilità” uno dei significati seguenti:

Il grado in cui un sistema, un sottosistema o un'apparecchiatura si trova in uno stato specificato di funzionamento e utilizzabilità all'inizio di una missione, quando la missione viene richiesta in un momento sconosciuto, ovvero casuale. In breve, la disponibilità è il periodo di tempo durante cui un sistema si trova in una condizione di funzionamento. Ciò viene spesso descritto come tasso di idoneità missione ed è espresso matematicamente come 1 meno indisponibilità.
La frequenza (a) del tempo totale per cui un'unità operativa è in grado di essere utilizzata durante un determinato intervallo rispetto (b) alla lunghezza dell'intervallo.

Nei termini della teoria delle probabilità, entrambe le definizioni hanno lo stesso significato, ovvero la probabilità che un determinato sistema o componente sia “operativo” o “in grado di essere utilizzato”, ovvero disponibile, in un qualsiasi momento casuale del tempo, ovvero nel momento in cui viene testato.

A livello matematico è possibile misurare questo valore, calcolando la quantità di tempo in cui il sistema risulta disponibile (“tempo di attività”) nel corso di un lungo periodo statisticamente significativo (in genere un anno) e dividendo il valore ottenuto per la lunghezza totale del periodo. Utilizzando la terminologia ampiamente adottata, ovvero Tempo medio tra errori (MTBF, Mean Time Between Failures) e Tempo medio per riparazione (MTTR, Mean Time To Repair), in cui il primo termine rappresenta la disponibilità o il tempo di attività del sistema tra gli errori, mentre il secondo indica il tempo di inattività del sistema durante un determinato errore, la disponibilità può essere espressa come una frazione:

La caratteristica matematica opposta sarebbe una probabilità di errore, ovvero una “non disponibilità”:

La disponibilità viene spesso espressa come “numero di nove”, in base alla tabella seguente:

Livello di disponibilità	Valore di disponibilità	Probabilità di errore	Tempo di inattività accettato all'anno
Due nove	99%	1%	5256 minuti = 3,65 giorni
Tre nove	99,9%	0,1%	525,6 minuti = 8,76 ore
Quattro nove	99,99%	0,01%	52,56 minuti
Cinque nove	99,999%	0,001%	5,26 minuti

Ovviamente, il valore relativo alla disponibilità risulta diverso se si prendono in considerazione il tempo di inattività sia pianificato (programmato) sia non pianificato (non programmato) oppure solo il tempo di inattività non pianificato. Il Contratto di servizio che rappresenta i requisiti di disponibilità aziendale deve essere molto specifico in merito. In tutti i casi, la disponibilità di un determinato sistema o componente dipende da molti fattori ed è essenziale identificare e comprendere tali dipendenze e il rispettivo impatto sulla disponibilità.

Impatto delle dipendenze del servizio sulla disponibilità

La disponibilità del database di cassette postali di Exchange dipende dalla disponibilità di molti altri servizi e componenti, ad esempio il sottosistema di archiviazione che ospita il database, il server che utilizza tale database, la connettività di rete a questo server e così via. Tutti questi componenti sono critici e l'errore di uno solo di tali componenti comporterebbe la perdita di servizio, anche se il database stesso non presenta alcun problema. Ciò significa che per rendere disponibile il database come servizio, è necessario che sia disponibile anche ogni singola dipendenza del database. Se si identificano e si isolano adeguatamente i componenti della dipendenza, sarà possibile calcolare matematicamente il modo in cui determinano la disponibilità risultante del database di cassette postali di Exchange.

Per un determinato database di cassette postali di Exchange, i componenti seguenti possono essere considerati dipendenze critiche:

Disco database / sottosistema di archiviazione: si supponga che la disponibilità sia A₁.
Server Cassette postali (componenti hardware e software): si supponga che la disponibilità sia A₂.
Server Accesso client (componenti hardware e software): è necessario ricordare che in Exchange 2010 tutti i client si connettono al database di cassette postali solo tramite il server Accesso client. Si supponga che in questo caso il server Accesso client sia installato separatamente rispetto al server Cassette postali e che la disponibilità sia A₃.
Connettività di rete tra client e server Accesso client e tra il server Accesso client e il server Cassette postali: si supponga che la disponibilità sia A₄.
Alimentazione nel datacenter in cui si trovano i server e l'archiviazione: si supponga che la disponibilità sia A₅.

Questo elenco potrebbe continuare ancora. Ad esempio, sia Active Directory sia DNS rappresentano dipendenze critiche per Exchange. Inoltre, in aggiunta alle dipendenze puramente tecnologiche, la disponibilità viene influenzata dalle dipendenze dei processi, ad esempio la maturità operativa e così via. L'errore umano, operazioni definite in modo errato, mancanza di coordinazione del team potrebbero provocare tempi di inattività del servizio. Non tenteremo di compilare qui un elenco completo delle dipendenze, ma ci concentreremo sul modo in cui influiscono sulla disponibilità complessiva del servizio.

Poiché questi stessi componenti sono individualmente indipendenti gli uni dagli altri, la disponibilità di ogni componente rappresenta un evento indipendente e la disponibilità risultante di un database di cassette postali di Exchange rappresenta una combinazione di tutti questi eventi. In altre parole, per consentire la disponibilità di un database di cassette postali per i client, è necessario che siano disponibili tutti questi componenti. In base alla teoria delle probabilità, la probabilità di una combinazione di eventi indipendenti è il prodotto delle singole probabilità per ogni evento:

Ad esempio, se si lanciano tre monete, la probabilità di ottenere testa su tutte e tre le monete è (1/2)*(1/2)*(1/2) = 1/8.

È importante comprendere che, poiché ogni valore di disponibilità non può essere maggiore di 1 (o 100%) e la disponibilità risultante del servizio è semplicemente un prodotto delle disponibilità dei singoli componenti, il valore di disponibilità risultante non può essere maggiore del più piccolo valore delle disponibilità dei componenti dipendenti.

Ciò può essere illustrato mediante l'esempio disponibile nella tabella seguente. I numeri riportati sono esemplificativi ma abbastanza realistici:

Componente dipendenza critica	Probabilità di errore	Valore disponibilità
Server Cassette postali e archiviazione	5%	95%
Server Accesso client	1%	99%
Rete	0,5%	99,5%
Alimentazione	0,1%	99,9%
Servizio complessivo (dipende da tutti i componenti riportati sopra)	6,51383%	95% x 99% x 99,5% x 99,9% = 93,48617%

In base a questo esempio è possibile notare quanto siano importanti le dipendenze dei servizi. Anche per un database di cassette normali che non presenta mai errori, ovvero non viene mai danneggiato e non viene mai infettato da virus e così via, la disponibilità rimane comunque inferiore al 93,5%.

Conclusione: un numero elevato di dipendenze dei servizi comporta una riduzione della disponibilità.

Qualsiasi intervento volto alla riduzione del numero o dell'impatto delle dipendenze dei servizi influirà positivamente sulla disponibilità complessiva dei servizi. Ad esempio, è possibile migliorare la maturità operativa semplificando e proteggendo la gestione dei server e ottimizzando le procedure operative. Per quanto riguarda l'aspetto tecnico, è possibile tentare di ridurre il numero di dipendenze dei servizi semplificando la progettazione, ad esempio eliminando progettazioni complesse di archiviazione basata su SAN, inclusi schede HBA, switch a fibre ottiche, controller di array e persino controller RAID e sostituendo tale progettazione con una semplice progettazione DAS con un numero minimo di parti mobili.

È possibile che la sola riduzione delle dipendenze dei servizi non sia sufficiente per portare la disponibilità al livello desiderato. Un altro modo molto efficiente per incrementare la disponibilità risultante e ridurre al minimo l'impatto delle dipendenze critiche dei servizi consiste nell'avvalersi di diversi metodi di ridondanza, ad esempio utilizzando fonti di alimentazioni doppie, schede di rete in team, connettendo i server a più switch di rete, utilizzando la protezione RAID per il sistema operativo, distribuendo servizi di bilanciamento del carico per server Accesso client e per più copie dei database di cassette postali. Ma in che modo esattamente la ridondanza incrementa la disponibilità? Di seguito vengono fornite informazioni più dettagliate sul caricamento del carico e sull'utilizzo di più copie di database come esempi importanti.

Impatto della ridondanza sulla disponibilità

A livello concettuale, tutti i metodi di ridondanza hanno un unico significato, ovvero la presenza di più di una istanza del componente che risulta disponibile e può essere utilizzata simultaneamente ad altre istanze, ad esempio nel bilanciamento del carico, o come sostituzione, ad esempio nel caso delle copie multiple del database. Si supponga di disporre di n istanze di un determinato componente, ovvero n server in un array di tipo CAS oppure n copie del database in DAG. Anche in caso di errore di una di tali istanze, le altre istanze possono essere comunque utilizzate, mantenendo pertanto la disponibilità. L'unica situazione che presenta effettivamente tempo di inattività è l'errore di tutte le istanze.

Come specificato in precedenza, la probabilità di errore per una determinata istanza è P = 1 – A. Tutte le istanze sono statisticamente indipendenti le une dalle altre. La disponibilità o l'errore di una delle istanze non influisce pertanto sulla disponibilità delle altre istanze. Ad esempio, l'errore di una determinata copia del database non influisce sulla probabilità di errore di un'altra copia del database, anche se è possibile che si verifichi il caso di un danneggiamento del database logico che si propaga dalla prima copia danneggiata del database a tutte le altre copie, ma per il momento questo fattore altamente improbabile verrà ignorato. Per risolvere tale problema è infatti possibile implementare una copia differita del database o un backup tradizionale temporizzato.

Utilizzando ancora lo stesso teorema della teoria delle probabilità, la probabilità di errore di una serie di n componenti indipendenti è un prodotto delle probabilità per ogni componente. Poiché in questo caso tutti i componenti sono identici, ovvero sono istanze diverse dello stesso oggetto, il prodotto diventa una potenza:

Apparentemente, poiché P < 1, Pⁿ è minore di P, che significa che la probabilità di errore diminuisce e, pertanto, la disponibilità aumenta:

Per chiarire, prendiamo in esame alcuni esempi della vita reale. Si supponga di distribuire più copie del database di cassette postali. Ogni copia è ospitata in una singola unità SATA. Statisticamente, la frequenza di errori delle unità SATA è pari a ~5% nel corso di un anno[1], che fornisce come risultato una probabilità di errore pari al 5%: P = 0,05 (ovvero disponibilità pari al 95%: A = 0.95). Per capire in che modo la disponibilità cambia quando si aggiungono più copie del database, esaminare la tabella esplicativa seguente:

Numero di copie del database	Probabilità di errore	Valore disponibilità
1	P₁ = P = 5%	A₁ = 1 – P₁ = 95%
2	P₂ = P² = 0,25%	A₂ = 1 – P₂ = 99,75%
3	P₃ = P³ = 0,0125%	A₃ = 1 – P₃ = 99,9875%
4	P₄ = P⁴ = 0,000625%	A₄ = 1 – P₄ = 99,9994%

Tutto ciò è decisamente interessante. In pratica, ogni copia aggiuntiva del database sull'unità SATA introduce il fattore di moltiplicazione 5% o 1/20, pertanto la probabilità di errore diminuisce 20 volte a ogni copia aggiunta, con un conseguente incremento della disponibilità. È possibile notare che anche nelle unità SATA più inaffidabili la distribuzione di 4 sole copie del database incrementa fino a cinque nove la disponibilità del database.

Si tratta di un risultato molto valido, ma ci si chiede se sia possibile renderlo ancora migliore e incrementare ulteriormente la disponibilità senza apportare modifiche a livello di architettura, ad esempio nel caso in cui l'aggiunta di un'altra copia del database non sia possibile.

Ciò è in effetti possibile. Se si ottimizza la disponibilità individuale di qualsiasi componente di dipendenza, ciò contribuirà all'incremento della disponibilità complessiva dei servizi e consentirà di ottenere un effetto maggiore mediante l'aggiunta di componenti ridondanti. Ad esempio, una soluzione possibile per ottenere questo risultato a costi ridotti consiste nell'utilizzo di unità SAS Nearline SAS invece di unità SATA. Le unità SAS Nearline hanno una frequenza di errori annuali pari a ~2,75% invece di ~5% delle unità SATA. Ciò ridurrà la probabilità di errore per il componente di archiviazione nel calcolo precedente e pertanto incrementerà la disponibilità complessiva dei servizi. È possibile confrontare l'impatto dell'aggiunta di più copie del database:

5% AFR = fattore di moltiplicazione 1/20 = ogni nuova copia rende un errore del database 20 volte meno probabile.
2,75% AFR = fattore di moltiplicazione 1/36 = ogni nuova copia rende un errore del database 36 volte meno probabile.

Questo impatto significativo delle copie aggiuntive del database sulla disponibilità del database spiega anche le nostre indicazioni in merito all'utilizzo di Exchange Native Data Protection, nelle quali si specifica che copie multiple del database possono costituire una sostituzione per i backup tradizionali se viene distribuito un numero sufficiente, ovvero tre o più, di copie del database.

La stessa logica si applica alla distribuzione di più server Accesso client in un array CAS, di più switch di rete e così via. Si supponga di avere distribuito quattro copie del database e quattro server Accesso client e si utilizzi di nuovo la tabella della disponibilità analizzata in precedenza:

Componente dipendenza critica	Probabilità di errore	Valore disponibilità
Server Cassette postali e archiviazione (4 copie)	5% ^ 4 = 0,000625%	99,999375%
Server Accesso client (4 server, installati separatamente)	1% ^ 4 = 0,000001%	99,999999%
Rete	0,5%	99,5%
Alimentazione	0,1%	99,9%
Servizio complessivo (dipende da tutti i componenti precedenti)	0,6%	99,399878%

Come si può notare, la semplice distribuzione di quattro server Accesso client e quattro copie del database consente di ridurre la probabilità di errore complessiva del servizio di oltre 10 volte (da 6,5% a 0,6%) e di incrementare di conseguenza la disponibilità dei servizi da 93,5% a un valore più apprezzabile pari a 99,4%.

Conclusione: l'aggiunta di ridondanza alle dipendenze dei servizi incrementa la disponibilità.

Considerazioni finali

Le conclusioni precedenti generano una domanda interessante. L'analisi di due fattori diversi che influiscono sulla disponibilità complessiva dei servizi in due modi diversi ha portato a due chiare conclusioni:

L'aggiunta di più dipendenze del sistema riduce la disponibilità
L'aggiunta di ridondanza alle dipendenze del sistema incrementa la disponibilità

Che cosa accade se entrambi sono fattori di una determinata soluzione? Quale tendenza è preponderante?

Si consideri lo scenario seguente:

Si distribuiscono due server Cassette postali in un gruppo di disponibilità del database con due copie del database di cassette postali, ovvero una copia in ogni server, e si distribuiscono due server Accesso client in un array con bilanciamento del carico. Per semplificare, prenderemo in considerazione solo la disponibilità di un database di cassette postali per le connessioni client, non prendendo per il momento in esame Trasporto Hub e Messaggistica unificata. Se si suppone che ogni server abbia una probabilità individuale di errore pari a P, la disponibilità di un tale sistema sarà superiore o inferiore a quella di un singolo server autonomo di Exchange in cui sono distribuiti sia il ruolo server Cassette postali sia il ruolo server Accesso client?

Nel primo scenario i server Cassette postali sono indipendenti e risulteranno non disponibili solo in caso di errore di entrambi i server. La probabilità di errore per l'insieme di due server Cassette postali sarà P × P = P². La disponibilità sarà pertanto A_MBX = 1 – P². In base alla stessa logica, i servizi CAS saranno non disponibili solo in caso di errore di entrambi i server Accesso client. La probabilità di errore per l'insieme di due server Accesso client sarà pertanto P × P = P² e la rispettiva disponibilità sarà A_CAS = 1 – P².

In questo caso, come si avrà notato, i due server Cassette postali o i due server Accesso client sono esempi di componenti ridondanti del sistema.

Procedendo con questo scenario, per consentire la disponibilità dell'intero sistema, è necessario che entrambi gli insiemi di server, ovvero l'insieme di server Cassette postali e l'insieme di server Accesso client, siano disponibili contemporaneamente. Non che presentino contemporaneamente un errore, ma che siano disponibili contemporaneamente, poiché ora rappresentano dipendenze del sistema invece di componenti ridondanti. Ciò significa che la disponibilità complessiva dei servizi è un prodotto delle disponibilità di ogni insieme:

Ovviamente, il secondo scenario è molto più semplice, poiché è necessario prendere in considerazione un solo server, la cui disponibilità è semplicemente A = 1 – P.

Avendo calcolato i valori di disponibilità per entrambi gli scenari, è necessario determinare quale valore sia superiore, ovvero (1-P²)² o 1-P.

Se si tracciano i grafici di entrambe le funzioni, si otterrà il comportamento seguente:

Per tracciare in modo rapido e semplice i grafici, è stato utilizzato il motore di calcolo gratuito Wolfram Alpha Mathematica Online.

Si può notare che per i valori ridotti di P la disponibilità del sistema complesso a 4 server è superiore alla disponibilità del singolo server. Ciò non ci sorprende, poiché si tratta di un risultato previsto. Tuttavia, con P ~ 0,618 (più precisamente, 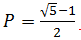) i due tracciati si incrociano e per valori superiori di P il sistema a server singolo presenta effettivamente una disponibilità superiore. Nel mondo reale ci si aspetta ovviamente che il valore di P sia molto vicino allo zero. Se tuttavia si prevede di creare una soluzione utilizzando componenti molto inaffidabili., sarà probabilmente consigliabile utilizzare un singolo server.

Impatto dei domini di errore

Sfortunatamente, gli scenari di distribuzione nel mondo reale presentano raramente la stessa semplicità delle situazioni illustrate in precedenza. Ad esempio, in che modo viene modificata la disponibilità dei servizi se si distribuiscono server a ruoli multipli? Nello scenario precedente si nota che la combinazione dei ruoli server consente di ridurre effettivamente il numero di dipendenze dei sistemi. Tale combinazione è quindi positiva? Che accade se si posizionano due copie dello stesso database nello stesso array SAN o enclosure DAS? Che accade se tutti i server Cassette postali sono connessi allo stesso switch di rete? E se si verificano tutte le condizioni indicate e altro ancora?

Tutte queste situazioni affrontano il concetto relativo ai domini di errore. Negli esempi precedenti un dominio di errore è rappresentato da hardware server, un array SAN o uno switch di rete. Il dominio di errore interrompe l'indipendenza o la ridondanza dei componenti in esso combinati. Ad esempio, un errore di hardware server in un server a ruoli multipli significa che tutti i ruoli di Exchange in tale server risulteranno non disponibili. Analogamente, un errore di un enclosure di dischi o un array SAN significa che tutte le copie di database ospitate in tale enclosure o array risulteranno non disponibili.

I domini di errore non sono necessariamente negativi. La differenza importante riguarda il tipo di componenti che costituiscono un dominio di errore, ovvero se si tratta di dipendenze di sistemi diversi o di componenti ridondanti del sistema. Per comprendere questa differenza, esamineremo due degli esempi precedenti.

Scenario con server a ruoli multipli

Di seguito viene effettuato un confronto tra la disponibilità dei due sistemi diversi

Entrambi i ruoli server Cassette postali e Accesso client sono ospitati nello stesso server con probabilità di errore hardware pari a P.
Gli stessi ruoli sono ospitati su due server separati, ognuno con la stessa probabilità di errore hardware.

Nel primo caso, l'hardware di un singolo server rappresenta un dominio di errore. Ciò significa che tutti i ruoli ospitati risultano tutti disponibili o tutti non disponibili. È molto semplice: la disponibilità complessiva di un sistema di questo tipo è A = 1 – P.

Nel secondo caso, il servizio complessivo sarà disponibile solo quando entrambi i server sono disponibili indipendentemente, poiché ogni ruolo rappresenta una dipendenza critica. In base alla teoria delle probabilità, la disponibilità sarà pertanto A × A = A².

Anche in questo caso, poiché A < 1, si ottiene che A² < A, pertanto la disponibilità nel secondo caso sarà inferiore.

È apparentemente possibile aggiungere altri ruoli server di Exchange (Trasporto Hub e Messaggistica unificata, se necessario) allo stesso scenario senza violare tale logica.

Conclusione: il posizionamento di ruoli server di Exchange in un server a ruoli multipli incrementa la disponibilità complessiva dei servizi.

Scenario di archiviazione condivisa

Si prenda ora in esame un altro scenario di dominio di errore, ovvero due copie di database che condividono lo stesso array di archiviazione, e si proceda al confronto della disponibilità dei database nei due casi seguenti:

Due copie di database sono ospitate nella stessa archiviazione condivisa, ovvero array SAN o enclosure DAS, con probabilità di errore P.
Le stesse copie di database sono ospitate in due sistemi di archiviazione distinti, ognuno dei quali ha la stessa probabilità di errore.

Nel primo caso, l'archiviazione condivisa rappresenta un dominio di errore. Analogamente allo scenario precedente, ciò significa che entrambe le copie del database sono disponibili o non disponibili contemporaneamente. La disponibilità complessiva è pertanto anche in questo caso A = 1 – P.

Nel secondo caso, il servizio complessivo risulterà disponibile se almeno uno dei sistemi è disponibile e risulterà non disponibile solo in caso di errore di entrambi i sistemi. I sistemi di archiviazione in questione sono indipendenti. La probabilità di errore del sistema complessivo è pertanto P × P = P² e la disponibilità complessiva del servizio è quindi A = 1 – P².

Anche in questo caso, poiché P < 1, si ottiene che P² < P e pertanto 1 – P² > 1 – P. Ciò significa che la disponibilità nel secondo caso è superiore.

Conclusione: il posizionamento di copie di database nello stesso sistema di archiviazione riduce la disponibilità complessiva del servizio.

Qual è quindi la differenza tra questi due scenari e perché l'introduzione di un dominio di errore incrementa la disponibilità nel primo caso mentre la riduce nel secondo caso?

Ciò dipende dal fatto che il dominio di errore nel primo caso combina dipendenze dei servizi, riducendone effettivamente il numero e migliorando pertanto la disponibilità, mentre il dominio di errore nel secondo caso combina componenti ridondanti, riducendo effettivamente la ridondanza e compromettendo pertanto la disponibilità.

È probabilmente possibile visualizzare come segue tutti questi concetti e le relative conclusioni:

Per tracciare questo grafico non abbiamo ovviamente utilizzato Wolfram Alpha.

Riepilogo

L'architettura di Exchange 2010 offre straordinarie possibilità per l'aggiunta di ridondanza a livello di Exchange, ad esempio la distribuzione di più copie di database o di più server Accesso client in un array CAS, e per la riduzione del numero di dipendenze del sistema, mediante la combinazione di ruoli server di Exchange in un server a ruoli multipli o mediante l'utilizzo di un'architettura di archiviazione più semplice, senza un numero eccessivo di componenti critici. Le semplici regole e formule presentate in questo articolo consentono di calcolare l'effetto sul valore di disponibilità ottenuto dalla distribuzione di copie di database aggiuntive o dalla combinazione di ruoli server di Exchange. È inoltre possibile calcolare l'impatto dei domini di errore. È importante notare che si è tentato di utilizzare questi semplici modelli matematici per illustrare i concetti, non per ottenere valori precisi di disponibilità. Il mondo reale si adatta raramente a semplici scenari di base e sono necessari calcoli molto più complessi per ottenere stime ragionevoli della disponibilità dei sistemi effettivi. Potrebbe risultare più semplice misurare semplicemente statisticamente la disponibilità e verificare se soddisfa i requisiti del Contratto di servizio. La comprensione dei fattori che influiscono sulla disponibilità e del modo in cui interagiscono in una soluzione di progettazione complessa consente tuttavia di agevolare una progettazione appropriata della soluzione e di ottenere un incremento significativo nella disponibilità complessiva dei servizi, in modo da soddisfare anche i requisiti aziendali più rigorosi.

Boris Lokhvitsky
Delivery Architect

[1] Gli studi seguenti eseguiti da Carnegie Mellon University, Google e Microsoft Research mostrano 5% AFR per unità SATA:

https://www.usenix.org/events/fast07/tech/schroeder/schroeder.pdf

https://labs.google.com/papers/disk_failures.pdf

https://research.microsoft.com/research/pubs/view.aspx?msr_tr_id=MSR-TR-2005-166