Curve dei parametri
I parametri multimediali sono in grado di seguire una curva nel tempo. Ogni curva è descritta da una formula matematica e da due punti finali. Ogni punto finale viene definito da un'ora di riferimento e dal valore della curva in quel momento. La formula viene utilizzata per calcolare i valori intermedi tra i punti e determina la forma della curva. Le curve possibili sono:
- Saltare
- Lineari
- Square
- Quadrato inverso
- Seno
"Jump" significa passare direttamente al valore finale. Le altre curve sono illustrate nel diagramma seguente.
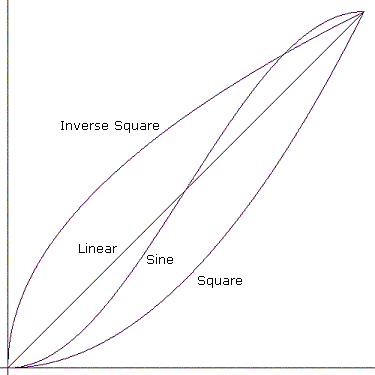
Matematicamente, le curve funzionano nel modo seguente. Si supponga che una curva inizi al momento t₀ con un valore v₀ e termina al momento t₁ con un valore v₁. I due punti che definiscono la curva sono (t₀, v₀) e (t₁, v₁).
- Lasciare che la durata totale della curva sia t₁-t₀.
- Lasciare che ₀ sia l'intervallo tra i valori iniziale e finale, v₁-v₀.
- In qualsiasi momento tin modo che t₀ <= t<₁, let Δt' = t-t₀.
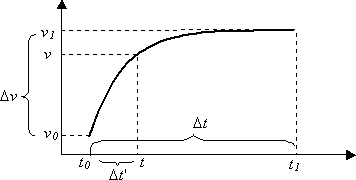
Il valore del parametro al momento t è:
v = f( ' /) *₀ +
dove f(x) è una funzione determinata dal tipo di curva:
- Lineare: y = x
- Quadrato: y = x^2
- Quadrato inverso: y = sqrt(x)
- Seno: y = [ sin(πx – π/2) + 1 ] / 2
Osservare che Δt' <Δt, quindi il termine Δt'/Δt varia da 0 a 1. Pertanto, f(x) varia anche da 0 a 1 e v cade sempre tra v₀ e v₁. Ciò vale se v₀ <v₁ o viceversa. In altre parole, la curva è delimitata dal rettangolo (t₀, v₀, t₁, v₁).
Per la curva seno, il valore di (πx – π/2) varia da –π/2 a π/2, il che significa che sin(πx – π/2) è compreso tra -1 e 1. Il risultato viene quindi normalizzato in modo che f(x) rientra nell'intervallo (0-1).
Argomenti correlati