Equazioni PRT (Direct3D 9)
Per comprendere appieno uno shader che implementa il token di aggiornamento primario, è utile derivare la formula usata dallo shader per calcolare la luminosità di uscita.
Per iniziare, l'equazione seguente è l'equazione generale per calcolare la luminosità di uscita risultante dall'illuminazione diretta su un oggetto diffuso con illuminazione distante arbitraria.
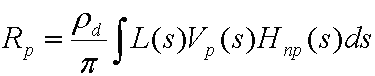
dove:
| Parametro | Descrizione |
|---|---|
| Rp | Raggi di uscita al vertice p. Valutata a ogni vertice della mesh. |
| pd | L'albedo della superficie. |
| pi | Costante, utilizzata come fattore di normalizzazione della conservazione dell'energia. |
| L/i | Ambiente di illuminazione (raggi di sorgente). |
| Vp₍s₎ | Funzione di visibilità binaria per il punto p. È 1 se il punto può vedere la luce, 0 in caso contrario. |
| Hnp₍s₎ | Il termine coseno dalla legge di Lambert. Uguale a max(Np· s), 0) dove Np è la normale superficie in corrispondenza del punto p. |
| s | Variabile che si integra sulla sfera. |
Usando funzioni di base sferica, ad esempio armonica sferica, l'equazione seguente approssima l'ambiente di illuminazione.
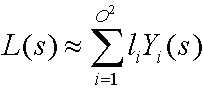
dove:
| Parametro | Descrizione |
|---|---|
| L/i | Ambiente di illuminazione (raggi di sorgente). |
| i | Intero che somma il numero di funzioni di base. |
| O | Ordine delle armonica sferica. |
| li | Coefficiente. |
| Yi(s) | Alcune funzioni di base sulla sfera. |
La raccolta di questi coefficienti, L', fornisce l'approssimazione ottimale per la funzione L(s) con le funzioni di base Y(s). La sostituzione e la distribuzione producono l'equazione seguente.
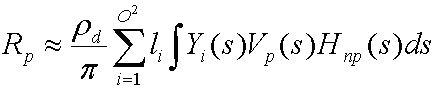
L'integrale di Yi(s)Vp₍s₎Hnp₍s₎ è un coefficiente di trasferimento tpi che il simulatore precomputa per ogni vertice nella mesh. La sostituzione di questo risultato restituisce l'equazione seguente.
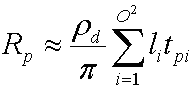
Se si modifica questa proprietà in notazione vettoriale, viene restituita l'equazione non compressa seguente per calcolare la luminosità di uscita per ogni canale.
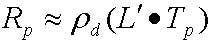
dove:
| Parametro | Descrizione |
|---|---|
| Rp | Raggi di uscita al vertice p. |
| pd | L'albedo della superficie. |
| L' | Il vettore di li ed è la proiezione della radiazione di origine nelle funzioni di base armonica sferica. Si tratta di un vettore order² di coefficienti armonici sferici. |
| Tp | Vettore di trasferimento order² per vertex p. Il simulatore divide i coefficienti di trasferimento per p. |
Entrambi questi vettori sono un vettore order² di coefficienti armonici sferici, quindi si noti che si tratta semplicemente di un prodotto punto. A seconda dell'ordine, il punto può essere costoso in modo da poter usare la compressione. Un algoritmo denominato Clustered Principal Component Analysis (CPCA) comprime in modo efficiente i dati. Ciò consente l'uso di un'approssimazione armonica a ordinamento superiore che produce ombre più nitide.
CPCA fornisce l'equazione seguente per approssimare il vettore di trasferimento.
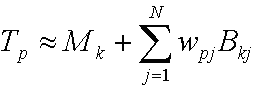
dove:
| Parametro | Descrizione |
|---|---|
| Tp | Vettore di trasferimento per vertex p. |
| Mk | Media per il cluster k. |
| j | Intero che somma il numero di vettori PCA. |
| N | Numero di vettori PCA. |
| w pj | Peso jth PCA per il punto p. |
| Broute | Vettore di base jth PCA per il cluster k. |
Un cluster è semplicemente un numero di vertici che condividono lo stesso vettore medio. Come ottenere la media del cluster, i pesi PCA, i vettori di base PCA e gli ID cluster per i vertici sono descritti di seguito.
Sostituendo queste due equazioni, si ottiene:
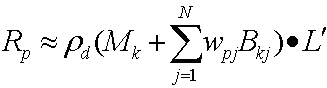
La distribuzione del prodotto punto produce quindi l'equazione seguente.
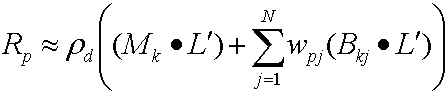
Perché entrambi (Mk· L') e (Bø· L') sono costanti per vertice, l'esempio calcola questi valori con la CPU e li passa come costanti nel vertex shader; poichéw pj cambia per ogni vertice, l'esempio archivia questi dati per vertice nel vertex buffer.
Argomenti correlati