Vettori, vertici e quaternioni

In Direct3D, i vertici descrivono la posizione e l'orientamento. Ogni vertice in una primitiva è descritto da un vettore che fornisce la posizione, il colore, le coordinate della trama e un vettore normale che ne fornisce l'orientamento.

I quaternioni aggiungono un quarto elemento ai valori [x, y, z] che definiscono un vettore a tre componenti. I quaternioni sono un'alternativa ai metodi matrice usati in genere per le rotazioni 3D. Un quaternione rappresenta un asse nello spazio tridimensionale e una rotazione intorno a tale asse. Un quaternione può rappresentare ad esempio un asse (1,1,2) e una rotazione di 1 radiante. I quaternioni contengono informazioni preziose, ma la loro vera potenza deriva dalle due operazioni che è possibile eseguire su di essi: composizione e interpolazione.

L'esecuzione di composizione su quaternioni è simile alla combinazione. La composizione di due quaternioni è notata come nella figura seguente.

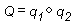
La composizione di due quaternioni applicata a una geometria significa "ruotare la geometria attorno all'asse₂ per rotazione₂, quindi ruotarla attorno all'asse₁ per rotazione₁". In questo caso, Q rappresenta una rotazione attorno a un singolo asse che è il risultato dell'applicazione di q₂, quindi q₁ alla geometria.

Usando l'interpolazione quaternione, un'applicazione può calcolare un percorso uniforme e ragionevole da un asse e un orientamento a un altro. Di conseguenza, l'interpolazione tra q₁ e q** offre un modo semplice per animare da un orientamento all'altro.

Quando si utilizzano insieme la composizione e l'interpolazione, si ottiene un modo semplice per manipolare una geometria in un modo che appare complesso. Si supponga, ad esempio, di avere una geometria che si desidera ruotare su un determinato orientamento. Sai che vuoi ruotarlo di r₂ gradi attorno all'asse₂, quindi ruotarlo di r₁ gradi attorno all'asse₁, ma non conosci il quaternione finale. Grazie alla composizione, è possibile combinare le due rotazioni relative alla geometria per ottenere un singolo quaternione che costituisce il risultato. Quindi, potresti interpolare dal quaternione originale a quello composto per ottenere una transizione graduale dall'uno all'altro.

Argomenti correlati

Sistemi di coordinate e geometria