Valutazione di un modello di classificazione
Buona parte dell'apprendimento automatico riguarda la valutazione dell'adeguatezza dei modelli. Questa valutazione viene effettuata durante il training, per facilitare lo sviluppo del modello, e dopo il training, per valutare più facilmente se il modello può essere usato nel mondo reale. I modelli di classificazione richiedono una valutazione, proprio come i modelli di regressione, anche se la procedura di valutazione può talvolta essere un po' più complessa.
Ripasso sul costo
Tenere presente che durante il training viene calcolato il livello di inadeguatezza di un modello e questo fattore viene definito costo o perdita. Ad esempio, nella regressione lineare si usa spesso una metrica denominata errore quadratico medio (MSE). Per calcolare l'errore quadratico medio, la previsione viene confrontata con l'etichetta effettiva, quindi il valore della differenza viene elevato al quadrato e si considera la media del risultato. È possibile usare l'errore quadratico medio per adattarlo al modello e per verificarne l'adeguatezza.
Funzioni di costo per la classificazione
I modelli di classificazione verranno valutati in base alle probabilità di output, ad esempio il 40% di probabilità che si verifichi una valanga, o alle etichette finali, ovvero no avalanche o avalanche. L'uso delle probabilità di output può essere particolarmente vantaggioso durante il training. Qualsiasi minima variazione del modello si traduce in una variazione delle probabilità, anche se non è sufficiente per modificare la decisione finale. L'uso delle etichette finali per una funzione di costo è più utile se si vogliono stimare le prestazioni reali del modello, ad esempio con il set di test. Questo perché, nei casi d'uso reali, verranno usate le etichette finali, non le probabilità.
Perdita di log
La perdita logaritmica è una delle funzioni di costo più comuni per la classificazione semplice. La perdita logaritmica viene applicata alle probabilità di output. Analogamente all'errore quadratico medio, un numero limitato di errori comporta costo ridotto, mentre un numero maggiore di errori si traduce in costi elevati. Nel grafico seguente viene raffigurata la perdita logaritmica per un'etichetta in cui la risposta corretta era 0 (false).
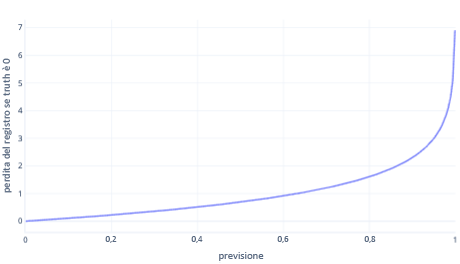
Sull'asse x sono rappresentati i possibili output del modello, ovvero le probabilità da 0 a 1, mentre l'asse y rappresenta il costo. Se un modello è estremamente sicuro che la risposta corretta sia 0 (ad esempio prevedendo 0,1), il costo è basso perché in questo caso la risposta corretta è 0. Se il modello prevede invece il risultato in modo errato (ad esempio prevedendo 0,9), il costo diventa molto elevato. In effetti, a x=1 il costo è talmente elevato che l'asse x viene ritagliato fino a 0,999 per garantire la leggibilità del grafico.
Perché non scegliere l'errore quadratico medio?
L'errore quadratico medio e la perdita logaritmica sono metriche simili. Esistono alcuni motivi complessi, ma anche altri più semplici, per cui preferire la perdita logaritmica per la regressione logistica. Ad esempio, la perdita logaritmica penalizza le risposte errate in modo più marcato rispetto all'errore quadratico medio. Nel grafico seguente, ad esempio, dove la risposta corretta è 0, il costo per le previsioni superiori a 0,8 è più elevato per la perdita logaritmica rispetto all'errore quadratico medio.
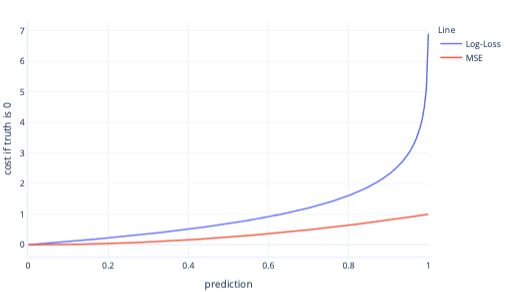
Se il costo è più elevato in questo modo, il training del modello è più veloce perché la gradiente della retta è molto più accentuato. Analogamente, con la perdita logaritmica è molto più probabile che i modelli forniscano la risposta corretta. Si noti nel grafico precedente che il costo dell'errore quadratico medio per i valori inferiori a 0,2 è piccolo e che il gradiente è quasi assente. A causa di questa relazione, il training risulta più lento per i modelli quasi corretti. La perdita logaritmica presenta un gradiente maggiore per questi valori e, di conseguenza, il training del modello è più veloce.
Limitazioni delle funzioni di costo
L'uso di una singola funzione di costo per la valutazione umana del modello è sempre limitato perché non consente di conoscere il tipo di errori commessi dal modello. Si consideri, ad esempio, lo scenario di previsione delle valanghe. Un valore di perdita logaritmica elevato può significare che il modello prevede ripetutamente le valanghe quando non se ne verificano oppure che non riesce a prevedere ripetutamente le valanghe quando si verificano.
Per comprendere meglio i modelli, può essere più semplice usare più di un valore per valutarne l'adeguatezza. Questo argomento verrà trattato in altro materiale didattico in modo più esteso, sebbene venga affrontato brevemente anche negli esercizi seguenti.