Confrontare e ottimizzare le curve ROC
Le curve ROC consentono di mettere a confronto i modelli e ottimizzare il modello selezionato. Analizziamo come vengono create e il motivo della loro utilità.
Ottimizzazione di un modello
L'uso più ovvio per una curva ROC consiste nella scelta di una soglia decisionale che garantisca prestazioni ottimali. Si ricordi che i modelli offrono gradi di probabilità, ad esempio il 65% di probabilità che il campione sia un escursionista. La soglia decisionale è il punto al di sopra del quale viene assegnato il valore true (escursionista) o al di sotto del quale viene assegnato il valore false (albero) a un campione. Se la soglia decisionale fosse del 50%, una probabilità del 65% verrebbe assegnata a true (escursionista). Se invece la soglia decisionale fosse del 70%, una probabilità del 65% sarebbe troppo bassa e verrebbe assegnata a false (albero).
Nell'esercizio precedente abbiamo visto che quando si crea una curva ROC, modifichiamo semplicemente la soglia decisionale e valutiamo il funzionamento del modello. Durante questa operazione, è possibile trovare la soglia che fornisce risultati ottimali.
In genere non esiste un'unica soglia in grado di offrire sia il tasso più alto di veri positivi (TPR, True Positive Rate) sia il tasso più basso di falsi positivi (FPR, False Positive Rate). La soglia ottimale dipende dal risultato che si vuole raggiungere. Ad esempio, in questo scenario è molto importante avere un tasso elevato di veri positivi poiché, se non viene identificato un escursionista durante una valanga, la squadra di salvataggio potrebbe non essere informata della presenza di una persona da salvare. Tuttavia, esiste anche il rischio del contrario: se il tasso di falsi positivi è troppo alto, la squadra di salvataggio potrebbe essere inviata ripetutamente a soccorrere escursionisti che in realtà non esistono. In altre situazioni, il tasso di falsi positivi è considerato più importante. Ad esempio, nel mondo scientifico c'è una bassa tolleranza per i risultati falsi positivi. Se il tasso di falsi positivi negli esperimenti scientifici fosse più elevato, ci troveremmo di fronte a una miriade di affermazioni contraddittorie, rendendo difficile distinguere ciò che è effettivamente reale.
Confronto di modelli con l'area sotto la curva
È possibile usare le curve ROC per confrontare i modelli tra loro, proprio come si fa con le funzioni di costo. La curva ROC di un modello mostra la sua efficacia per una serie di soglie decisionali. In fin dei conti, la cosa più importante in un modello è la sua efficienza nel mondo reale, in cui c'è un'unica soglia decisionale. Perché dunque è necessario confrontare i modelli usando soglie che non verranno mai usate? I motivi possibili sono due.
In primo luogo, confrontare le curve ROC in base a diverse soglie equivale a eseguire un test statistico che indica non solo che un modello ha avuto prestazioni migliori nello specifico set di test, ma anche se è probabile che le prestazioni continuino a migliorare in futuro. Questo concetto non rientra nell'ambito di questo materiale di apprendimento, ma vale la pena tenerlo presente.
In secondo luogo, la curva ROC mostra, in una certa misura, il grado di affidabilità del modello con la soglia perfetta. Se, ad esempio, il modello è affidabile solo quando si ha una soglia decisionale pari allo 0,9, ma non lo è affatto al di sopra o al di sotto di questo valore, significa che non è stato progettato correttamente. Probabilmente sarebbe ideale usare un modello che offra prestazioni consistenti attraverso diverse soglie, coscienti del fatto che, se i dati reali differiscono leggermente dal set di test, non si registreranno cali di prestazioni significativi.
In che modo confrontare le curve ROC?
Il modo più semplice per confrontare numericamente le curve ROC è quello di esaminare l'area sotto la curva, ovvero l'area del grafico che si trova al di sotto della curva. Ad esempio, il modello perfetto dell'ultimo esercizio ha un valore di area sotto la curva pari a 1:
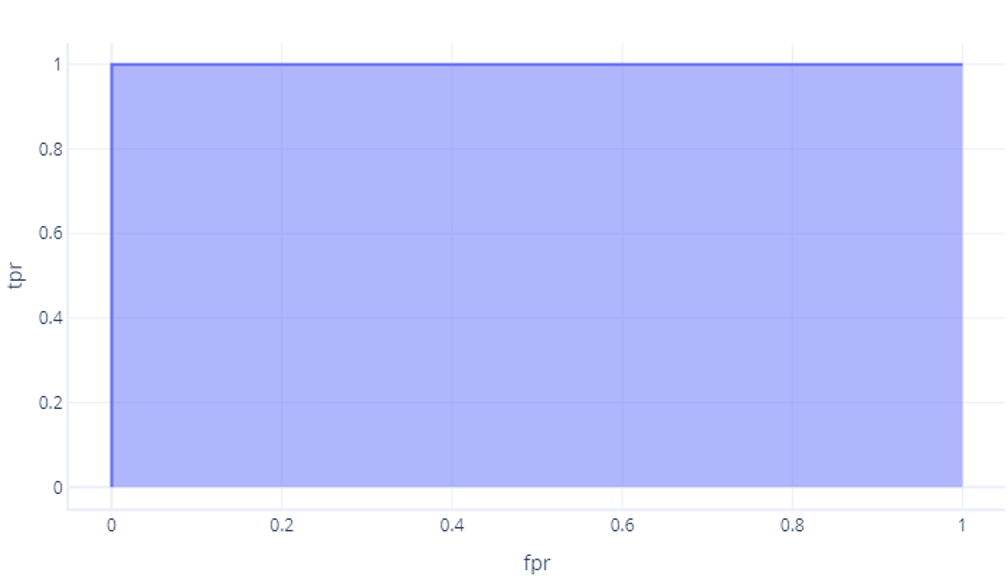
Il nostro modello, che non ha superato una previsione casuale, ha un'area di circa 0,5 sotto la curva:
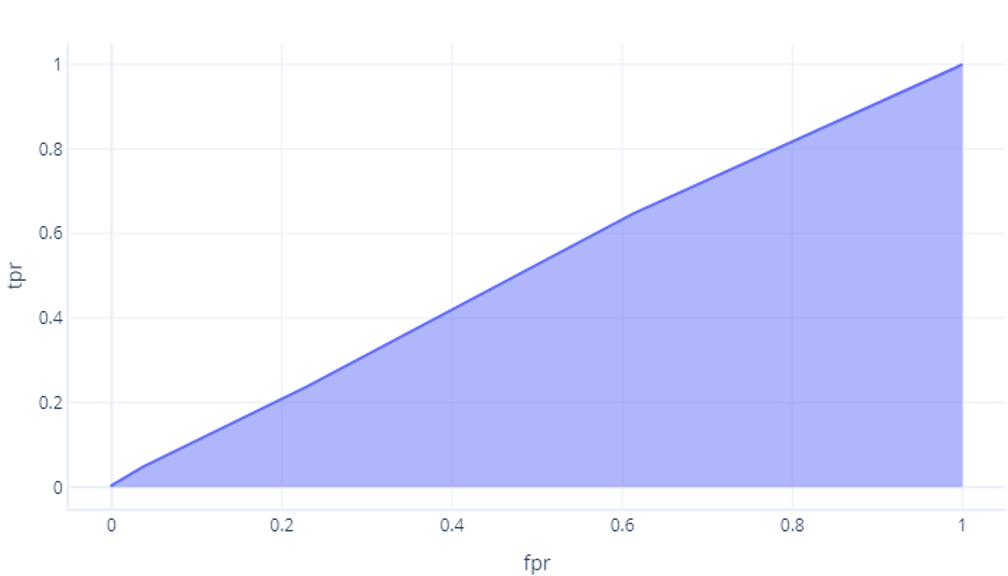
Più perfetto è il modello, più estesa diventa l'area. Se si ha un modello con un'area sotto la curva di grandi dimensioni, si è certi che funziona correttamente per un'ampia gamma di soglie e quindi ha probabilmente una buona struttura ed è stato sottoposto a un buon training. Al contrario, un modello con un'area sotto la curva ridotta (più vicina allo 0,5) non funziona correttamente.