Analizzare la classificazione con le curve delle caratteristiche operative del ricevitore
I modelli di classificazione devono assegnare un campione a una categoria. Ad esempio, per determinare se un oggetto è un escursionista o un albero, devono essere usate caratteristiche quali dimensioni, colore e movimento.
I modelli di classificazione possono essere migliorati in molti modi. È ad esempio possibile verificare che i dati siano bilanciati, puliti e dimensionati. È anche possibile modificare l'architettura del modello e usare iperparametri per ottenere le massime prestazioni dai dati e dall'architettura. Alla fine, quando non si riescono a trovare altri modi per migliorare le prestazioni nel set di test, si stabilisce che il modello è pronto.
L'ottimizzazione del modello a questo punto può essere complessa, ma è possibile ricorrere a un semplice passaggio finale per migliorare ulteriormente le prestazioni del modello. Per comprendere questa ultima possibilità, è tuttavia necessario tornare alle nozioni di base.
Probabilità e categorie
Molti modelli prevendono più fasi decisionali, di cui la finale è spesso semplicemente un passaggio di binarizzazione. Durante questo passaggio, le probabilità vengono convertite in un'etichetta fissa. Ad esempio, supponiamo che il modello sia dotato di determinate funzionalità e determini che ci sia una probabilità del 75% che venga mostrato un escursionista e una probabilità del 25% che venga mostrato un albero. Un oggetto non può essere al 75% un escursionista e al 25% un albero: o è l'uno o è l'altro. Pertanto, il modello applica una soglia, che in genere è pari al 50%. Se la classe dell'escursionista è superiore al 50%, l'oggetto viene identificato come escursionista.
La soglia del 50% rappresenta un criterio logico. In altre parole, viene sempre scelta l'etichetta più probabile in base al modello. Se tuttavia il modello presenta una distorsione, la soglia del 50% potrebbe non essere appropriata. Ad esempio, se il modello ha una leggera tendenza a identificare alberi piuttosto che escursionisti, selezionando alberi con una frequenza del 10% maggiore rispetto al necessario, è possibile correggere la soglia decisionale per compensare tale inclinazione.
Ripasso sulle matrici decisionali
Le matrici decisionali sono un ottimo modo per valutare i tipi di errori commessi da un modello. In questo modo vengono fornite le percentuali di veri positivi (TP), veri negativi (TN), falsi positivi (FP) e falsi negativi (FN)

Dalla matrice di confusione possono essere calcolate alcune caratteristiche utili, tra cui le due caratteristiche comuni seguenti:
- Tasso di veri positivi (sensibilità): la frequenza con cui le etichette "True" vengono identificate correttamente come "True". Ad esempio, la frequenza con cui il modello stima la presenza di un "escursionista" quando il campione mostrato è effettivamente un escursionista.
- Tasso di falsi positivi (tasso di falsi allarmi): la frequenza con cui le etichette "False" vengono erroneamente identificate come "True". Ad esempio, la frequenza con cui il modello stima la presenza di un "escursionista" quando viene mostrato un albero.
I tassi di veri positivi e falsi positivi possono aiutare a comprendere le prestazioni di un modello.
Si consideri l'esempio dell'escursionista. In teoria, il tasso di veri positivi è molto alto e quello di falsi positivi è molto basso, poiché il modello riconosce gli escursionisti con notevole accuratezza e raramente confonde gli alberi per escursionisti. Tuttavia, se il tasso di veri positivi è molto alto cosi come quello di falsi positivi, il modello non è bilanciato: identifica quasi tutto come escursionista. Analogamente, non è consigliabile usare un modello con un tasso di veri positivi basso, poiché potrebbe classificare erroneamente un escursionista come un albero.
Curve ROC
Le curve ROC sono rappresentate da un grafico in cui viene messo a confronto il tasso di veri positivi con il tasso di falsi positivi.
Tali curve possono risultare poco comprensibili ai principianti per due motivi principali. Il primo motivo è dato dal fatto che i principianti sanno che un modello ha un solo valore per i tassi di veri positivi e di veri negativi. Pertanto, un grafico ROC deve avere un aspetto simile al seguente:

Anche se può sembrare strano, un modello con training produce un solo punto. Tuttavia, è necessario tenere presente che i modelli hanno una soglia, in genere del 50%, che viene usata per decidere se usare l'etichetta true (escursionista) o false (albero). Se si modifica questa soglia impostando il 30% e si ricalcolano i tassi di veri positivi e falsi positivi, si ottiene un altro punto:
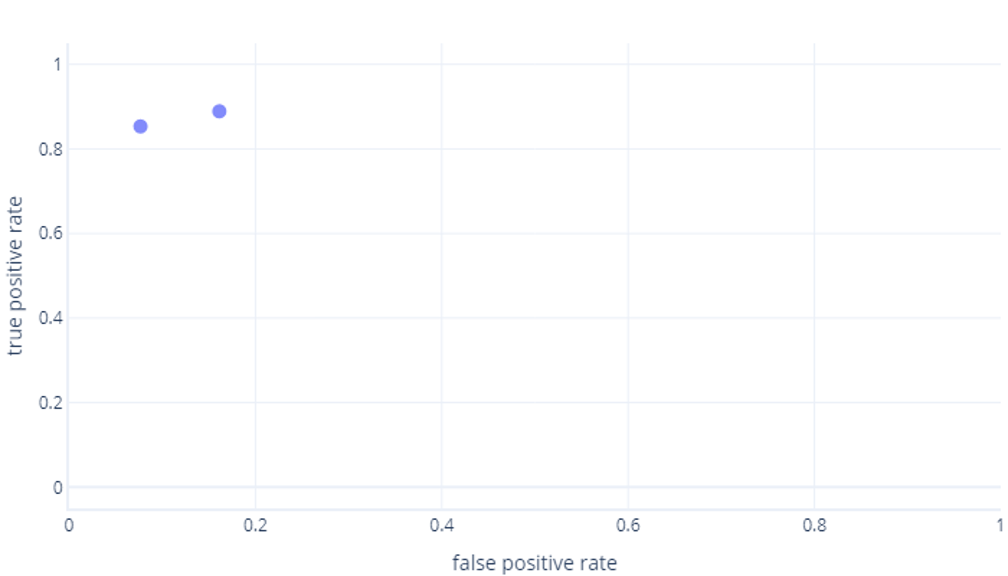
Se ripetiamo questa operazione per le soglie tra lo 0% e il 100%, si otterrà un grafico simile al seguente:
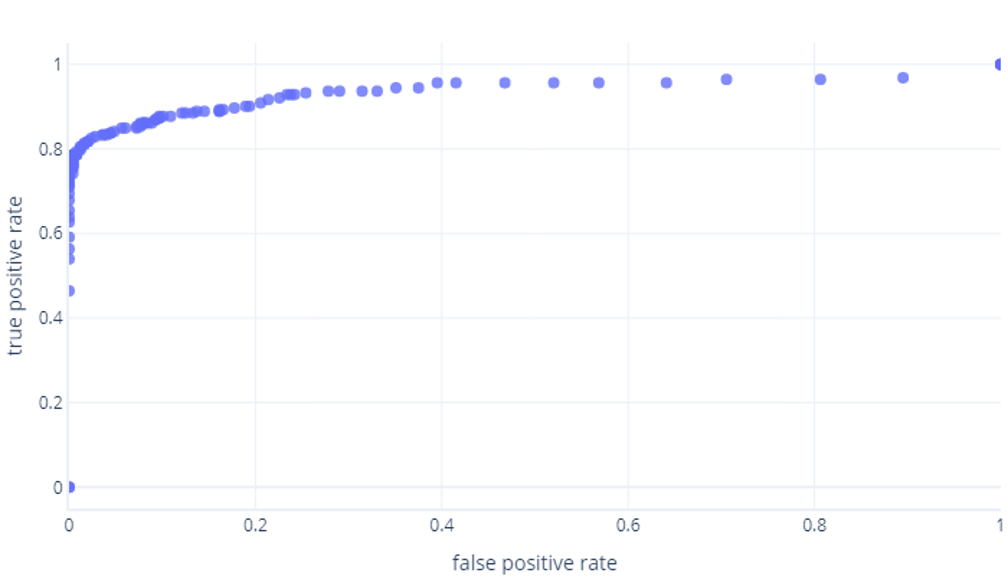
Questo grafico viene in genere rappresentato da una linea:
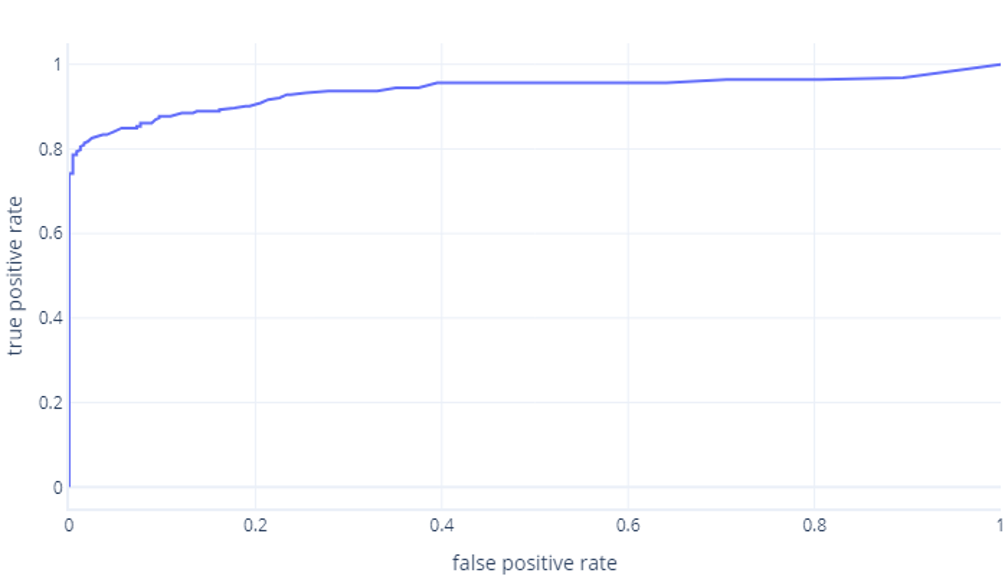
Il secondo motivo per cui questi grafici possono generare confusione è dato dalla terminologia specialistica usata per descriverli. Tenere presente che è necessario un alto tasso di veri positivi (gli escursionisti vengono identificati come tali) e un basso tasso di falsi positivi (gli alberi non vengono identificati come escursionisti).
Curve ROC più o meno attendibili
Per valutare le curve ROC in modo ottimale e distinguere le curve più attendibili da quelle meno attendibili è preferibile usare un ambiente interattivo. Passare quindi all'esercizio successivo per approfondire questo argomento.