Che cos'è la sovrapposizione nel calcolo quantistico?

  • 5 minuti

Se il gatto dell'unità precedente fosse stato un gatto quantistico, lo stato del gatto quantistico e del sistema contenitore sarebbero uguali: la somma delle sei diverse posizioni del gatto quantistico rispetto alla scatola, ponderata in base alla probabilità di trovare il gatto quantistico in tale posizione. L'unica differenza è che il gatto classico può essere in una (e solo una) di sei posizioni possibili, mentre il gatto quantistico può essere in tutte le sei posizioni contemporaneamente!

Nel mondo classico, gli oggetti possono trovarsi solo in uno stato alla volta. Tuttavia, nel mondo quantistico, le particelle quantistiche possono trovarsi in più stati contemporaneamente. Questo fenomeno è detto sovrapposizione.

Nel calcolo quantistico nessuno usa gatti quantistici, purtroppo, ma qubit. La parola "qubit" significa "bit quantistico". Proprio come nel calcolo classico, dove l'unità di base delle informazioni è il bit, nel calcolo quantistico l'unità di base di informazioni è il qubit. E proprio come il bit può accettare due valori possibili, 0 e 1, un qubit è qualsiasi particella quantistica che può essere in due stati possibili. Ad esempio, un qubit può essere un fotone, che può essere polarizzato in due direzioni, o un elettrone, che può essere in due livelli di energia.

Come si può rappresentare la sovrapposizione in un qubit? Qual è la probabilità di trovare un qubit in uno stato specifico?

Come si può rappresentare la sovrapposizione in un qubit?

Un qubit è una particella quantistica con due possibili posizioni o stati. Analogalmente al bit classico, gli stati quantistici di un qubit sono chiamati anche $0$ e $1$. Un qubit può trovarsi nello stato $0$, nello stato $1$, e in qualsiasi sovrapposizione di entrambi gli stati. Come si può rappresentare questa sovrapposizione?

Si supponga di disegnare un cerchio e un asse verticale e orizzontale in modo che il punto centrale sia il centro del cerchio. Lo stato $0$ viene posizionato al punto superiore dell'asse verticale e lo stato $1$ si trova nel punto inferiore.

Come si può descrivere questa rappresentazione? Si potrebbe dire che lo stato $0$ è una freccia o un vettore che punta verso l'alto e lo stato $1$ è un vettore che punta verso il basso. Pertanto, un bit classico sarebbe un vettore che punta verso l'alto o verso il basso, ma mai in un'altra direzione.

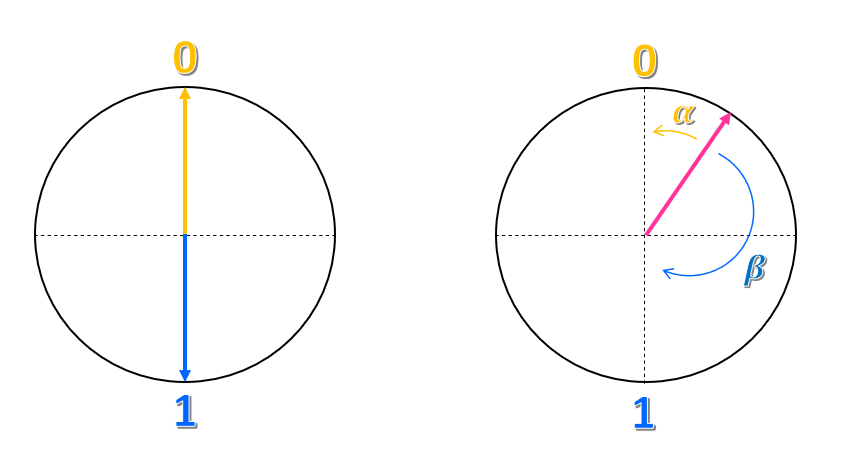
Diagramma di un cerchio con due frecce che puntano verso l'alto e verso il basso dal centro del cerchio. Le frecce rappresentano rispettivamente gli stati 0 e 1. Qualsiasi altro stato è una freccia che punta verso altre direzioni.

Che cosa dire di tutti gli altri punti del cerchio? Come si può rappresentare tale stato? Proprio come coordinate in un piano, è possibile provare a rappresentarlo come una combinazione dei due stati $0$ e $1$. Ad esempio, si potrebbe considerare quanto è vicino il vettore allo stato $0$ e chiamare quest'angolo $\alpha$, e quanto è vicino allo stato $1$ e chiamare questo angolo $\beta$. Potremmo rappresentare lo stato come $\alpha 0 + \beta 1 $. Di conseguenza, lo stato è una sovrapposizione degli stati $0$ e $1$.

Proprio come l'esempio del gatto e del contenitore, lo stato globale di un qubit è la somma dei singoli stati, $0$ e $1$, ponderato per la probabilità di trovare il qubit in tale stato, $\alpha$ e $\beta $.

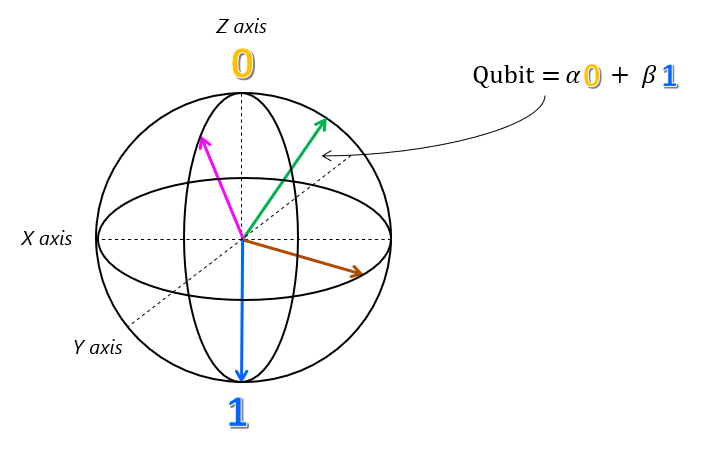
Diagramma della sfera di Bloch con stati 0 e 1 nell'asse z e altro vettore che rappresenta le combinazioni infinite di sovrapposizioni.

Questa rappresentazione di un qubit è effettivamente accurata ed è nota come Sfera di Bloch.

Suggerimento

La sfera di Bloch è uno strumento potente perché le operazioni che è possibile eseguire su un qubit possono essere rappresentate come rotazioni intorno a uno degli assi cardinali. Anche se pensare a un calcolo quantistico come una sequenza di rotazioni è un'idea potente, è difficile usare questa intuizione per progettare e descrivere gli algoritmi. Q# attenua questo problema fornendo un linguaggio per la descrizione di tali rotazioni.

Qual è la probabilità di trovare un qubit in uno stato?

Come nell'esempio del gatto e del contenitore dell'unità precedente, lo stato globale di un qubit è la somma dei singoli stati, $0$ e $1$, ponderato per la probabilità di trovare il qubit in tale stato, $\alpha$ e $\beta $. I numeri $\alpha$ e $\beta$ rappresentano quanto "vicino" lo stato del qubit è rispettivamente agli stati $0$ e $1$. Quindi, $\alpha$ e $\beta$ rappresentano la probabilità di trovare il qubit nello stato $0$ o $1$? Non esattamente.

I numeri $\alpha$ e $\beta$ sono ampiezze di probabilità per ogni stato. I valori assoluti, ad esempio$|\alpha|^2$, offrono le probabilità corrispondenti. Ad esempio, la probabilità di osservare lo stato $0$ è $|\alpha|^2$e la probabilità di osservare lo stato $1$ è $|\beta|^2$.

I numeri $\alpha$ e $\beta$ possono essere positivi, negativi o anche numeri complessi. Per una sovrapposizione quantistica valida, tuttavia, la somma di tutte le probabilità deve essere pari a uno: $|\alpha|^2+|\beta|^2=1$. Questo vincolo è detto condizione di normalizzazione. È possibile considerare la condizione di normalizzazione come il fatto che si ottiene sempre un risultato quando si effettua una misurazione, quindi le probabilità di misurare ogni possibile risultato devono essere sommate in una.