Come si usa l'entanglement per inviare informazioni?
Nelle unità precedenti si è appreso che l'entanglement quantistico può essere una risorsa eccellente per la comunicazione quantistica. In questa unità verrà visualizzata una delle applicazioni più famose dell'entanglement: il protocollo di teletrasporto quantistico.
Nel teletrasporto si usa l'entanglement per trasferire lo stato di un qubit da una posizione a un'altra. Lo stato del qubit viene trasferito a un altro qubit, ma il qubit stesso non viene spostato fisicamente. Questa è una cosa importante da ricordare. Le informazioni sullo stato del qubit vengono trasferite a un altro qubit usato come contenitore in cui scrivere le informazioni del qubit del messaggio.
Il protocollo di teletrasporto usa una combinazione di entanglement e comunicazione classica. La comunicazione classica è importante perché il protocollo di teletrasporto richiede al mittente di comunicare i risultati delle misurazioni al ricevitore. Ciò significa che il teletrasporto non può inviare informazioni più velocemente della velocità della luce. La comunicazione classica tra il mittente e il ricevitore è limitata dalla velocità della luce.
Si esaminerà ora il protocollo di teletrasporto quantistico.
Protocollo di teletrasporto quantistico
Alice e Bob lavorano insieme nella stessa azienda. Alice si trova a Seattle e Bob si trova a Los Angeles. Stanno lavorando a un progetto che richiede loro di condividere informazioni quantistiche. Decidono di usare il teletrasporto quantistico per inviare reciprocamente informazioni quantistiche.
Configurazione iniziale
Alice e Bob hanno ciascuno un qubit che fa parte di una coppia con entanglement preparata in precedenza. La coppia con entanglement è uno stato di Bell, ovvero lo stato
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice ha un qubit aggiuntivo denominato "qubit di messaggio", e vuole inviare questo qubit a Bob. Il qubit di messaggio si trova in uno stato sconosciuto che Alice vuole teletrasportare a Bob. Lo stato del qubit di messaggio è
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
dove $\alpha$ e $\beta$ sono numeri complessi.
Lo stato globale dei tre qubit di Alice e Bob è
$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$
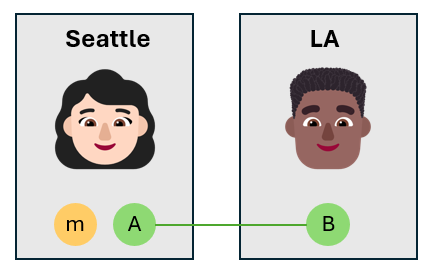
Alice sottopone a entanglement il qbit di messaggio con il proprio qubit
Alice accetta il qubit di messaggio e ne esegue l'entanglement con il proprio qubit $A$ usando una porta CNOT. Il qubit di messaggio è il qubit di controllo e il qubit di Alice è il qubit target. In questo modo viene creato uno stato con entanglement a tre qubit.
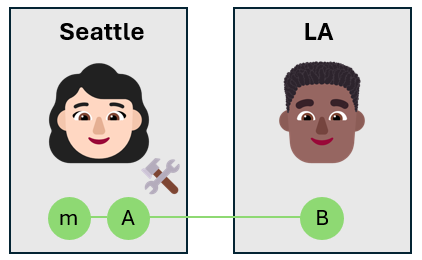
Il qubit di messaggio si trova nello stato sconosciuto $\alpha\ket{0}_m + \beta\ket{1}_m$, quindi dopo l'applicazione della porta CNOT, i qubit di Alice si trovano in una sovrapposizione dei quattro stati di Bell. Lo stato globale dei tre qubit è
$$\ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$
$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$
$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Lo stato globale dei qubit di Alice e Bob è una sovrapposizione di quattro stati possibili.
Suggerimento
Un buon esercizio consiste nel verificare che lo stato globale dei tre qubit sia quello indicato in precedenza. A tale scopo, è possibile applicare la porta CNOT al qubit di messaggio e al qubit di Alice e quindi espandere lo stato dei tre qubit.
Alice misura i qubit
Alice misura quindi il qubit di messaggio e il proprio qubit. Non misura i qubit nella base $Z$ come di consueto, ma sceglie la base Bell. La base Bell è costituita dai quattro stati di Bell, $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-} \rbrace$.
Misurando il qubit di messaggio e il proprio qubit nella base Bell, Alice proietta i qubit in uno dei quattro stati di Bell. Poiché i tre qubit presentano entanglement, i risultati della misurazione sono correlati. Quando Alice misura i propri qubit, anche il qubit di Bob viene proiettato nello stato correlato.
Ad esempio, se Alice misura i propri qubit e osserva lo stato $\ket{\phi^-}$, il qubit di Bob viene proiettato nello stato $\alpha\ket{0}_B - \beta\ket{1}_B$.
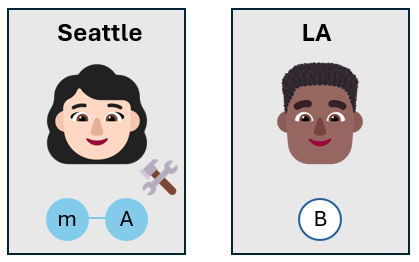
Alice chiama Bob
Alice chiama Bob e gli comunica i risultati delle sue misurazioni. Usa un canale di comunicazione classico, ad esempio una telefonata o un SMS.
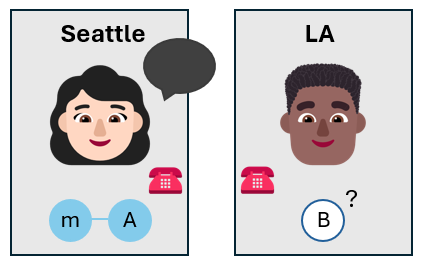
Bob ora conosce lo stato del proprio qubit, senza doverlo misurare. Lo stato del qubit di Bob potrebbe non essere uguale allo stato del qubit di messaggio che Alice voleva teletrasportare, ma è abbastanza vicino.
Bob applica un'operazione quantistica
Bob può quindi recuperare lo stato originale del qubit di messaggio applicando un'operazione quantistica specifica al qubit. L'operazione eseguita da Bob dipende da ciò che Alice gli ha detto al telefono.
L'operazione eseguita può essere una porta Pauli $X$, una porta Pauli $Z$, entrambe o nessuna.
Ad esempio, se il risultato della misurazione di Alice è $\ket{\phi^-}$, Bob sa che il qubit si trova nello stato $(\alpha\ket{0}_B - \beta\ket{1}_B)$. Deve semplicemente applicare una porta Pauli Z per recuperare lo stato originale del qubit di messaggio.
| Alice misura | Bob applica |
|---|---|
| $\ket{\phi^+}$ | Nessuna operazione |
| $\ket{\phi^-}$ | Porta Pauli Z |
| $\ket{\psi^+}$ | Porta Pauli X |
| $\ket{\psi^-}$ | Porta Pauli X seguita dalla porta Pauli Z |
Questa operazione finale teletrasporta effettivamente lo stato del qubit di messaggio nel qubit di Bob. Missione completata.
Importante
L'applicazione di un'operazione a un qubit non equivale a misurarla. Quando Bob applica l'operazione, non misura il qubit. Applica un'operazione quantistica che modifica lo stato del qubit, ma non lo collassa.