Cos'è l'entanglement?
L'entanglement è una delle principali caratteristiche della meccanica quantistica e la distingue dalla meccanica classica. Ma che cos'è l'entanglement? Come funziona? E perché è così importante per le informazioni quantistiche?
In questa unità si vedrà come definire e descrivere l'entanglement quantistico e capire perché è una risorsa così potente per il calcolo quantistico.
Informazioni sull'entanglement quantistico
Si supponga di avere due qubit, $A$ e $B$. I qubit sono indipendenti l'uno dall'altro, il che significa che le informazioni sullo stato del qubit $A$, qualunque sia, appartengono solo al qubit $A$. Analogamente, le informazioni sullo stato del qubit $B$ appartengono al qubit $B$. È possibile descrivere lo stato di ogni qubit. In questo caso, i qubit sono senza entanglement, perché non condividono informazioni.
Si supponga ora di applicare l'entanglement ai qubit. Si apprenderà come eseguire questa operazione in un secondo momento. Se i qubit $A$ e $B$ sono sottoposti a entanglement, le informazioni sullo stato del qubit $A$ non sono indipendenti dallo stato dielqubit $B$. Con l'entanglement, le informazioni vengono condivise tra entrambi i qubit e non è possibile dedurre lo stato del qubit $A$ o lo stato del qubit $B$. È solo possibile descrivere lo stato del sistema globale, non lo stato dei singoli qubit.
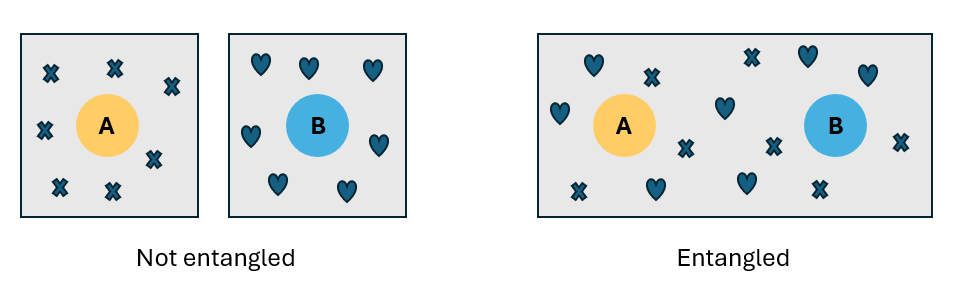
L'entanglement è una correlazione quantistica tra due o più particelle. Se due particelle sono sottoposte a entanglement, non possono essere descritte in modo indipendente, ma solo come intero sistema.
Descrizione dell'entanglement quantistico
Si immaginino due qubit $A$ e $B$ configurati in modo che lo stato del sistema globale $\ket{\phi}$ sia:
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B})$$
Nota
In notazione Dirac, $\ket{0_A 0_B}=|0\rangle_\text{A}|0\rangle_\text{B}$. La prima posizione corrisponde al primo qubit e la seconda posizione corrisponde al secondo qubit.
Il sistema globale $\ket{\phi}$ si trova in una sovrapposizione degli stati $|00\rangle$ e $|11\rangle$. Se si misurano entrambi i qubit, sono possibili solo due risultati: $\ket{{00}$ e $\ket{{11}$ e ognuno ha la stessa probabilità di $\frac{1}{{2}$.
Ma qual è lo stato individuale del qubit $A$? E del qubit $B$? Se si prova a descrivere lo stato del qubit $A$ senza considerare lo stato del qubit $B$, si verifica un errore. I sottosistemi $A$ e $B$ sono stati sottoposti a entanglement, il che significa che sono correlati e non possono essere descritti in modo indipendente.
Suggerimento
Se si ha familiarità con l'algebra e la notazione Dirac, un buon esercizio consiste nel provare a modificare lo stato $\ket{\phi}$ per ottenere qualcosa come lo stato del qubit $A$ moltiplicato per lo stato del qubit $B$. Se prova a espandere la parentesi, ottenere il fattore comune e così via, si noterà che non è possibile.
Lo stato quantistico $\ket{\phi}$ è uno stato con entanglement speciale, denominato stato di Bell. Esistono quattro stati di Bell.
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$$$\ket{\phi^{-}}=\frac1{\sqrt2}\ket{00} - \frac1{\sqrt2}\ket{11}$$$$\ket{\psi^{+}}=\frac1{\sqrt2}\ket{{01} + \frac1{\sqrt2}\ket{{10}$$$$\ket{\psi^{-}}=\frac1{\sqrt2}\ket{01} - \frac1{\sqrt2}\ket{10}$$
Uso dell'entanglement come risorsa
A questo punto è possibile che ci si domandi perché l'entanglement è così importante.
Quando due particelle sono sottoposte a entanglement, i sottosistemi sono correlati e non possono essere descritti in modo indipendente. Ma ecco la parte interessante: anche i risultati della misurazione sono correlati. Ovvero, qualsiasi operazione venga eseguita sullo stato di un qubit in una coppia con entanglement influisce anche sullo stato dell'altro qubit.
Si consideri, ad esempio, lo stato $\ket{\phi^{+}}$:
$$\ket{\phi^{+}}=\frac1{\sqrt2}\ket{{00} + \frac1{\sqrt2}\ket{{11}$$
Se si misurano entrambi i qubit, si ottiene $|00\rangle$ o $|11\rangle$ con la stessa probabilità. Esiste una probabilità zero di ottenere gli stati $|01\rangle$ e $|10\rangle$.
Ma cosa accade se si misura un solo qubit?
Se si misura solo il qubit $A$ e si ottiene lo stato $|0\rangle$, significa che il sistema globale collassa allo stato $\ket{00}$. Questo è l'unico risultato possibile, poiché la probabilità di misurare $|01\rangle$ è zero.
Pertanto, senza misurare il qubit $B$ si può essere certi che anche il secondo qubit si trovi nello stato $|0\rangle$. I risultati della misura sono correlati a causa dell'entanglement dei qubit.
L'entanglement può esistere tra due particelle anche se sono separate da grandi distanze. Questa correlazione è più forte di qualsiasi correlazione classica ed è una risorsa chiave per le attività di elaborazione delle informazioni quantistiche, ad esempio teleportazione quantistica, crittografia quantistica e calcolo quantistico.