Tre modi per disegnare un arco

Informazioni su come usare SkiaSharp per definire gli archi in tre modi diversi

Un arco è una curva sulla circonferenza di un'ellisse, ad esempio le parti arrotondate di questo segno infinito:

Nonostante la semplicità di tale definizione, non c'è modo di definire una funzione di disegno ad arco che soddisfi ogni esigenza, e quindi, nessun consenso tra i sistemi grafici del modo migliore per disegnare un arco. Per questo motivo, la SKPath classe non si limita a un solo approccio.

SKPath definisce un AddArc metodo, cinque metodi diversi ArcTo e due metodi relativi RArcTo . Questi metodi rientrano in tre categorie, che rappresentano tre approcci molto diversi per specificare un arco. Quale si usa dipende dalle informazioni disponibili per definire l'arco e dal modo in cui questo arco si integra con l'altra grafica che si sta disegnando.

Arco angolo

L'approccio dell'arco dell'angolo agli archi di disegno richiede di specificare un rettangolo che delimita un'ellisse. L'arco sulla circonferenza di questa ellisse è indicato da angoli dal centro dell'ellisse che indicano l'inizio dell'arco e la sua lunghezza. Due diversi metodi disegnano archi di angolo. Si tratta del AddArc metodo e del ArcTo metodo :

public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)

public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)

Questi metodi sono identici ai metodi Android AddArc e [ArcTo]xref:Android.Graphics.Path.ArcTo*). Il metodo iOS AddArc è simile ma è limitato agli archi sulla circonferenza di un cerchio anziché generalizzato a un'ellisse.

Entrambi i metodi iniziano con un SKRect valore che definisce sia la posizione che le dimensioni di un'ellisse:

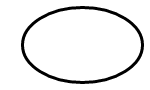
L'arco è una parte della circonferenza di questo ellisse.

L'argomento startAngle è un angolo in senso orario in gradi rispetto a una linea orizzontale disegnata dal centro dell'ellisse a destra. L'argomento sweepAngle è relativo all'oggetto startAngle. Di seguito sono riportati startAngle i valori e sweepAngle di 60 gradi e 100 gradi rispettivamente:

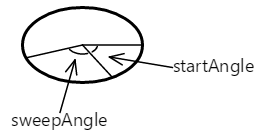
L'arco inizia all'angolo iniziale. La sua lunghezza è governata dall'angolo di sweep. L'arco è mostrato qui in rosso:

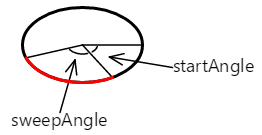
La curva aggiunta al percorso con il AddArc metodo o ArcTo è semplicemente quella parte della circonferenza dell'ellisse:

Gli startAngle argomenti o sweepAngle possono essere negativi: l'arco è in senso orario per i valori positivi di sweepAngle e in senso antiorario per i valori negativi.

Tuttavia, AddArc non definisce un contorno chiuso. Se si chiama LineTo dopo AddArc, viene disegnata una linea dalla fine dell'arco al punto nel LineTo metodo e lo stesso è true di ArcTo.

AddArc avvia automaticamente un nuovo contorno ed è funzionalmente equivalente a una chiamata a ArcTo con un argomento finale di true:

path.ArcTo (oval, startAngle, sweepAngle, true);

L'ultimo argomento viene chiamato forceMoveToed esegue in modo efficace una MoveTo chiamata all'inizio dell'arco. Inizia un nuovo contorno. Questo non è il caso con un ultimo argomento di false:

path.ArcTo (oval, startAngle, sweepAngle, false);

Questa versione di ArcTo disegna una linea dalla posizione corrente all'inizio dell'arco. Ciò significa che l'arco può essere da qualche parte nel mezzo di un contorno più grande.

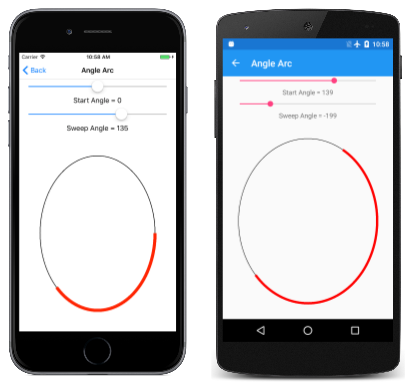
La pagina Angle Arc consente di usare due dispositivi di scorrimento per specificare gli angoli di inizio e sweep. Il file XAML crea un'istanza di due Slider elementi e un oggetto SKCanvasView. Il PaintCanvas gestore nel file AngleArcPage.xaml.cs disegna sia l'ovale che l'arco usando due SKPaint oggetti definiti come campi:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
    float startAngle = (float)startAngleSlider.Value;
    float sweepAngle = (float)sweepAngleSlider.Value;

    canvas.DrawOval(rect, outlinePaint);

    using (SKPath path = new SKPath())
    {
        path.AddArc(rect, startAngle, sweepAngle);
        canvas.DrawPath(path, arcPaint);
    }
}

Come si può notare, sia l'angolo iniziale che l'angolo di sweep possono assumere valori negativi:

Questo approccio alla generazione di un arco è algoritmicamente il più semplice ed è facile derivare le equazioni parametriche che descrivono l'arco. Conoscere le dimensioni e la posizione dell'ellisse e gli angoli iniziale e di sweep, i punti iniziale e finale dell'arco possono essere calcolati usando semplici trigonometria:

x = oval.MidX + (oval.Width / 2) * cos(angle)

y = oval.MidY + (oval.Height / 2) * sin(angle)

Il angle valore è startAngle o startAngle + sweepAngle.

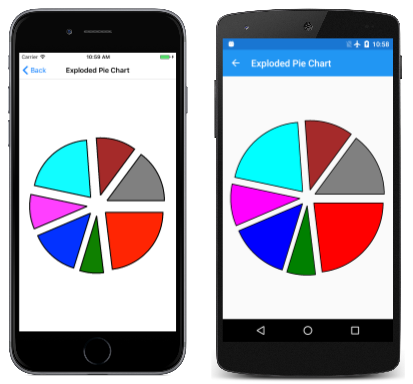
L'uso di due angoli per definire un arco è ideale per i casi in cui si conosce la lunghezza angolare dell'arco che si desidera disegnare, ad esempio, per creare un grafico a torta. La pagina Grafico a torta esplosa illustra questa operazione. La ExplodedPieChartPage classe usa una classe interna per definire alcuni dati e colori fabricati:

class ChartData
{
    public ChartData(int value, SKColor color)
    {
        Value = value;
        Color = color;
    }

    public int Value { private set; get; }

    public SKColor Color { private set; get; }
}

ChartData[] chartData =
{
    new ChartData(45, SKColors.Red),
    new ChartData(13, SKColors.Green),
    new ChartData(27, SKColors.Blue),
    new ChartData(19, SKColors.Magenta),
    new ChartData(40, SKColors.Cyan),
    new ChartData(22, SKColors.Brown),
    new ChartData(29, SKColors.Gray)
};

Il PaintSurface gestore esegue prima il ciclo degli elementi per calcolare un totalValues numero. In questo modo, può determinare le dimensioni di ogni elemento come frazione del totale e convertirlo in un angolo:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    int totalValues = 0;

    foreach (ChartData item in chartData)
    {
        totalValues += item.Value;
    }

    SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
    float explodeOffset = 50;
    float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
    SKRect rect = new SKRect(center.X - radius, center.Y - radius,
                             center.X + radius, center.Y + radius);

    float startAngle = 0;

    foreach (ChartData item in chartData)
    {
        float sweepAngle = 360f * item.Value / totalValues;

        using (SKPath path = new SKPath())
        using (SKPaint fillPaint = new SKPaint())
        using (SKPaint outlinePaint = new SKPaint())
        {
            path.MoveTo(center);
            path.ArcTo(rect, startAngle, sweepAngle, false);
            path.Close();

            fillPaint.Style = SKPaintStyle.Fill;
            fillPaint.Color = item.Color;

            outlinePaint.Style = SKPaintStyle.Stroke;
            outlinePaint.StrokeWidth = 5;
            outlinePaint.Color = SKColors.Black;

            // Calculate "explode" transform
            float angle = startAngle + 0.5f * sweepAngle;
            float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
            float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);

            canvas.Save();
            canvas.Translate(x, y);

            // Fill and stroke the path
            canvas.DrawPath(path, fillPaint);
            canvas.DrawPath(path, outlinePaint);
            canvas.Restore();
        }

        startAngle += sweepAngle;
    }
}

Viene creato un nuovo SKPath oggetto per ogni sezione della torta. Il percorso è costituito da una linea dal centro, quindi da un ArcTo oggetto per disegnare l'arco e da un'altra linea verso il centro risultati dalla Close chiamata. Questo programma visualizza le sezioni a torta "esplose" spostandole tutte dal centro di 50 pixel. Tale attività richiede un vettore nella direzione del punto intermedio dell'angolo di sweep per ogni sezione:

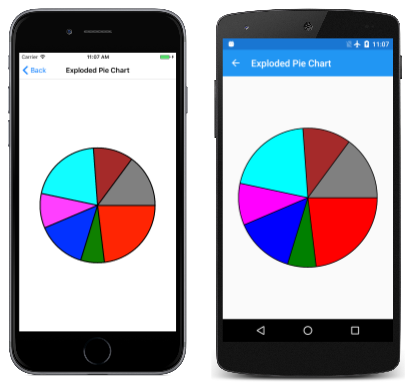
Per vedere come sembra senza l'esplosione, è sufficiente commentare la Translate chiamata:

Arco tangente

Il secondo tipo di arco supportato da SKPath è l'arco tangente, così chiamato perché l'arco è la circonferenza di un cerchio che è tangente a due linee collegate.

Un arco tangente viene aggiunto a un percorso con una chiamata al ArcTo metodo con due SKPoint parametri oppure l'overload ArcTo con parametri separati Single per i punti:

public void ArcTo (SKPoint point1, SKPoint point2, Single radius)

public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)

Questo ArcTo metodo è simile alla funzione PostScript arct (pagina 532) e al metodo iOS AddArcToPoint .

Il ArcTo metodo prevede tre punti:

• Punto corrente del contorno o punto (0, 0) se MoveTo non è stato chiamato
• Primo argomento punto del ArcTo metodo, denominato punto angolare
• Secondo argomento punto a ArcTo, denominato punto di destinazione:

Questi tre punti definiscono due linee collegate:

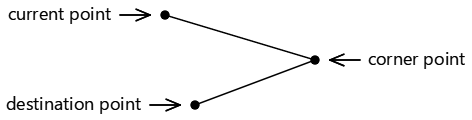
Se i tre punti sono colinear, ovvero se si trovano sulla stessa linea retta, non verrà disegnato alcun arco.

Il ArcTo metodo include anche un radius parametro . Questo definisce il raggio di un cerchio:

L'arco tangente non è generalizzato per un'ellisse.

Se le due linee si incontrano in qualsiasi angolo, tale cerchio può essere inserito tra tali linee in modo che sia tangente a entrambe le linee:

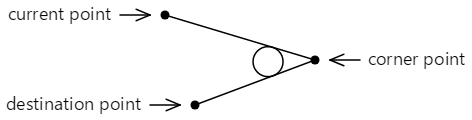
La curva aggiunta al contorno non tocca nessuno dei punti specificati nel ArcTo metodo . È costituito da una linea retta dal punto corrente al primo punto tangente e da un arco che termina al secondo punto tangente, mostrato qui in rosso:

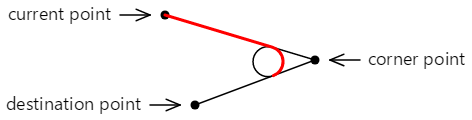
Ecco la linea retta finale e l'arco che viene aggiunto al contorno:

Il contorno può essere continuato dal secondo punto tangente.

La pagina Arco tangente consente di sperimentare l'arco tangente. Si tratta della prima di diverse pagine che derivano da InteractivePage, che definisce alcuni oggetti utili SKPaint ed esegue TouchPoint l'elaborazione:

public class InteractivePage : ContentPage
{
    protected SKCanvasView baseCanvasView;
    protected TouchPoint[] touchPoints;

    protected SKPaint strokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3
    };

    protected SKPaint redStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Red,
        StrokeWidth = 15
    };

    protected SKPaint dottedStrokePaint = new SKPaint
    {
        Style = SKPaintStyle.Stroke,
        Color = SKColors.Black,
        StrokeWidth = 3,
        PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
    };

    protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
    {
        bool touchPointMoved = false;

        foreach (TouchPoint touchPoint in touchPoints)
        {
            float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
            SKPoint point = new SKPoint(scale * (float)args.Location.X,
                                        scale * (float)args.Location.Y);
            touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
        }

        if (touchPointMoved)
        {
            baseCanvasView.InvalidateSurface();
        }
    }
}

La classe TangentArcPage deriva da InteractivePage. Il costruttore nel file TangentArcPage.xaml.cs è responsabile della creazione di istanze e dell'inizializzazione della touchPoints matrice e dell'impostazione baseCanvasView (in InteractivePage) sull'oggetto di cui è stata creata un'istanza SKCanvasView nel file TangentArcPage.xaml:

public partial class TangentArcPage : InteractivePage
{
    public TangentArcPage()
    {
        touchPoints = new TouchPoint[3];

        for (int i = 0; i < 3; i++)
        {
            TouchPoint touchPoint = new TouchPoint
            {
                Center = new SKPoint(i == 0 ? 100 : 500,
                                     i != 2 ? 100 : 500)
            };
            touchPoints[i] = touchPoint;
        }

        InitializeComponent();

        baseCanvasView = canvasView;
        radiusSlider.Value = 100;
    }

    void sliderValueChanged(object sender, ValueChangedEventArgs args)
    {
        if (canvasView != null)
        {
            canvasView.InvalidateSurface();
        }
    }
    ...
}

Il PaintSurface gestore usa il ArcTo metodo per disegnare l'arco in base ai punti di tocco e a , Sliderma calcola anche in modo algoritmico il cerchio su cui si basa l'angolo:

public partial class TangentArcPage : InteractivePage
{
    ...
    void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
    {
        SKImageInfo info = args.Info;
        SKSurface surface = args.Surface;
        SKCanvas canvas = surface.Canvas;

        canvas.Clear();

        // Draw the two lines that meet at an angle
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.LineTo(touchPoints[1].Center);
            path.LineTo(touchPoints[2].Center);
            canvas.DrawPath(path, dottedStrokePaint);
        }

        // Draw the circle that the arc wraps around
        float radius = (float)radiusSlider.Value;

        SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
        SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);

        double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
        double angleBetween = Math.Acos(dotProduct);
        float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
        SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
        SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
                                     touchPoints[1].Center.Y + vMid.Y * hypotenuse);

        canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);

        // Draw the tangent arc
        using (SKPath path = new SKPath())
        {
            path.MoveTo(touchPoints[0].Center);
            path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
            canvas.DrawPath(path, redStrokePaint);
        }

        foreach (TouchPoint touchPoint in touchPoints)
        {
            touchPoint.Paint(canvas);
        }
    }

    // Vector methods
    SKPoint Normalize(SKPoint v)
    {
        float magnitude = Magnitude(v);
        return new SKPoint(v.X / magnitude, v.Y / magnitude);
    }

    float Magnitude(SKPoint v)
    {
        return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
    }
}

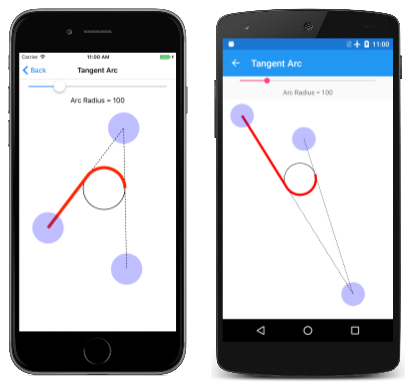
Ecco la pagina Arco tangente in esecuzione:

L'arco tangente è ideale per creare angoli arrotondati, ad esempio un rettangolo arrotondato. Poiché SKPath include già un AddRoundedRect metodo, nella pagina Eptagon arrotondato viene illustrato come utilizzare ArcTo per arrotondare gli angoli di un poligono a sette lati. Il codice è generalizzato per qualsiasi poligono regolare.

Il PaintSurface gestore della RoundedHeptagonPage classe contiene un for ciclo per calcolare le coordinate dei sette vertici dell'heptagon e un secondo per calcolare i punti intermedi dei sette lati da questi vertici. Questi punti intermedi vengono quindi usati per costruire il percorso:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    float cornerRadius = 100;
    int numVertices = 7;
    float radius = 0.45f * Math.Min(info.Width, info.Height);

    SKPoint[] vertices = new SKPoint[numVertices];
    SKPoint[] midPoints = new SKPoint[numVertices];

    double vertexAngle = -0.5f * Math.PI;       // straight up

    // Coordinates of the vertices of the polygon
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
                                       radius * (float)Math.Sin(vertexAngle));
        vertexAngle += 2 * Math.PI / numVertices;
    }

    // Coordinates of the midpoints of the sides connecting the vertices
    for (int vertex = 0; vertex < numVertices; vertex++)
    {
        int prevVertex = (vertex + numVertices - 1) % numVertices;
        midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
                                        (vertices[prevVertex].Y + vertices[vertex].Y) / 2);
    }

    // Create the path
    using (SKPath path = new SKPath())
    {
        // Begin at the first midpoint
        path.MoveTo(midPoints[0]);

        for (int vertex = 0; vertex < numVertices; vertex++)
        {
            SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];

            // Draws a line from the current point, and then the arc
            path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);

            // Connect the arc with the next midpoint
            path.LineTo(nextMidPoint);
        }
        path.Close();

        // Render the path in the center of the screen
        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 10;

            canvas.Translate(info.Width / 2, info.Height / 2);
            canvas.DrawPath(path, paint);
        }
    }
}

Ecco il programma in esecuzione:

Arco ellittico

L'arco ellittico viene aggiunto a un percorso con una chiamata al ArcTo metodo con due SKPoint parametri oppure l'overload ArcTo con coordinate X e Y separate:

public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)

public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)

L'arco ellittico è coerente con l'arco ellittico incluso in Scalable Vector Graphics (SVG) e la classe piattaforma UWP (Universal Windows Platform)ArcSegment.

Questi ArcTo metodi tracciano un arco tra due punti, ovvero il punto corrente del contorno, e l'ultimo parametro al ArcTo metodo (il xy parametro o i parametri e y separatix):

Il primo parametro punto del ArcTo metodo (r, o rx e ry) non è un punto, ma specifica invece i raggi orizzontali e verticali di un'ellisse;

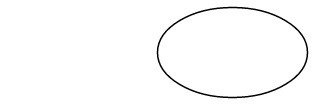
Il xAxisRotate parametro è il numero di gradi in senso orario per ruotare l'ellisse seguente:

Se l'ellisse inclinata viene quindi posizionata in modo che tocchi i due punti, i punti sono collegati da due archi diversi:

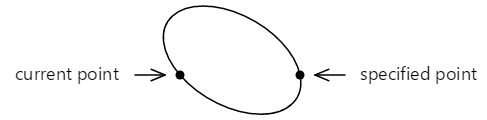
Questi due archi possono essere distinti in due modi: l'arco superiore è maggiore dell'arco inferiore e, man mano che l'arco viene disegnato da sinistra a destra, l'arco superiore viene disegnato in senso orario mentre l'arco inferiore viene disegnato in senso antiorario.

È anche possibile adattare l'ellisse tra i due punti in un altro modo:

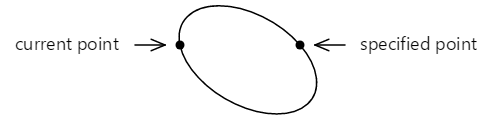
Ora c'è un arco più piccolo in alto che viene disegnato in senso orario e un arco più grande sul fondo disegnato in senso antiorario.

Questi due punti possono quindi essere collegati da un arco definito dall'ellisse inclinata in un totale di quattro modi:

Questi quattro archi sono distinti dalle quattro combinazioni degli argomenti del SKPathArcSize tipo di enumerazione SKPathDirection al ArcTo metodo :

• red: SKPathArcSize.Large e SKPathDirection.Clockwise
• verde: SKPathArcSize.Small e SKPathDirection.Clockwise
• blue: SKPathArcSize.Small e SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large e SKPathDirection.CounterClockwise

Se l'ellisse inclinata non è abbastanza grande da adattarsi tra i due punti, viene ridimensionato uniformemente fino a quando non è abbastanza grande. In questo caso, solo due archi univoci collegano i due punti. Questi valori possono essere distinti con il SKPathDirection parametro .

Anche se questo approccio alla definizione di un arco suona complesso al primo incontro, è l'unico approccio che consente di definire un arco con un'ellisse ruotata, ed è spesso l'approccio più semplice quando è necessario integrare archi con altre parti del contorno.

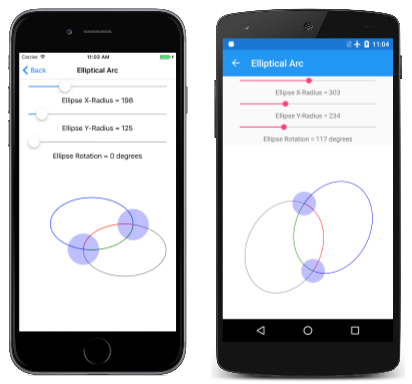
La pagina Arco ellittico consente di impostare in modo interattivo i due punti e le dimensioni e la rotazione dell'ellisse. La EllipticalArcPage classe deriva da InteractivePagee il PaintSurface gestore nel file code-behind EllipticalArcPage.xaml.cs disegna i quattro archi:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        int colorIndex = 0;
        SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
                                          (float)yRadiusSlider.Value);
        float rotation = (float)rotationSlider.Value;

        foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
            foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
            {
                path.MoveTo(touchPoints[0].Center);
                path.ArcTo(ellipseSize, rotation,
                           arcSize, direction,
                           touchPoints[1].Center);

                strokePaint.Color = colors[colorIndex++];
                canvas.DrawPath(path, strokePaint);
                path.Reset();
            }
    }

    foreach (TouchPoint touchPoint in touchPoints)
    {
        touchPoint.Paint(canvas);
    }
}

Di seguito è in esecuzione:

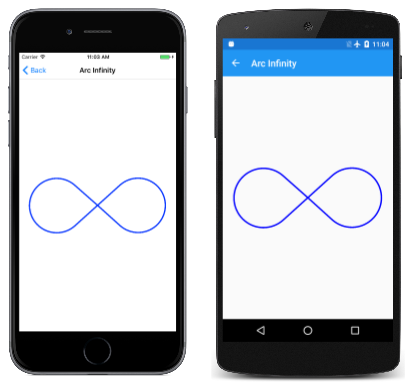
La pagina Arc Infinity usa l'arco ellittico per disegnare un segno infinito. Il segno infinito si basa su due cerchi con raggi di 100 unità separate da 100 unità:

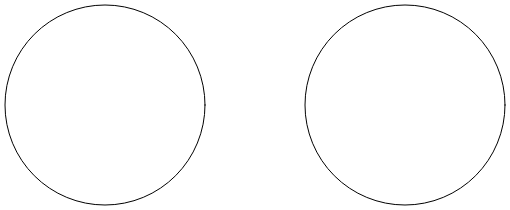
Due linee che si incrociano tra loro sono tangenti a entrambi i cerchi:

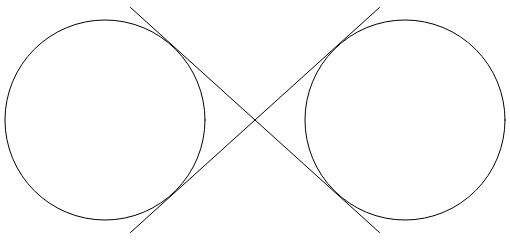
Il segno infinito è una combinazione di parti di questi cerchi e le due linee. Per utilizzare l'arco ellittico per disegnare il segno infinito, è necessario determinare le coordinate in cui le due linee sono tangenti ai cerchi.

Costruire un rettangolo destro in uno dei cerchi:

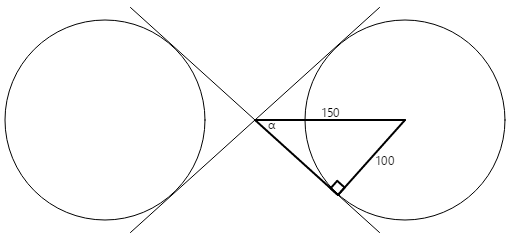
Il raggio del cerchio è 100 unità e l'ipotenusa del triangolo è di 150 unità, quindi l'angolo α è l'arcosine (seno inverso) di 100 diviso per 150 o 41,8 gradi. La lunghezza dell'altro lato del triangolo è 150 volte il coseno di 41,8 gradi, o 112, che può essere calcolato anche dal teorema pitagorico.

Le coordinate del punto tangente possono quindi essere calcolate usando queste informazioni:

x = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

I quattro punti tangenti sono tutti necessari per disegnare un segno infinito centrato sul punto (0, 0) con raggi circolari di 100:

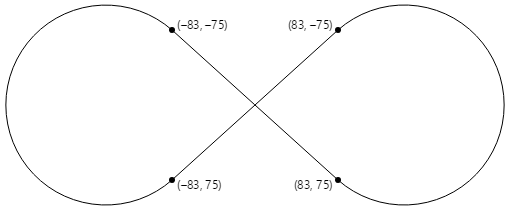
Il PaintSurface gestore nella ArcInfinityPage classe posiziona il segno infinito in modo che il punto (0, 0) sia posizionato al centro della pagina e ridimensiona il percorso alla dimensione dello schermo:

void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
    SKImageInfo info = args.Info;
    SKSurface surface = args.Surface;
    SKCanvas canvas = surface.Canvas;

    canvas.Clear();

    using (SKPath path = new SKPath())
    {
        path.LineTo(83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
        path.LineTo(-83, 75);
        path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
        path.Close();

        // Use path.TightBounds for coordinates without control points
        SKRect pathBounds = path.Bounds;

        canvas.Translate(info.Width / 2, info.Height / 2);
        canvas.Scale(Math.Min(info.Width / pathBounds.Width,
                              info.Height / pathBounds.Height));

        using (SKPaint paint = new SKPaint())
        {
            paint.Style = SKPaintStyle.Stroke;
            paint.Color = SKColors.Blue;
            paint.StrokeWidth = 5;

            canvas.DrawPath(path, paint);
        }
    }
}

Il codice usa la Bounds proprietà di SKPath per determinare le dimensioni del seno infinito per ridimensionarlo alle dimensioni dell'area di disegno:

Il risultato sembra un po ' piccolo, che suggerisce che la Bounds proprietà di SKPath segnala una dimensione maggiore del percorso.

Internamente, Skia approssima l'arco usando più curve quadratiche di Bézier. Queste curve (come si vedrà nella sezione successiva) contengono punti di controllo che regolano il modo in cui viene disegnata la curva, ma non fanno parte della curva sottoposta a rendering. La Bounds proprietà include tali punti di controllo.

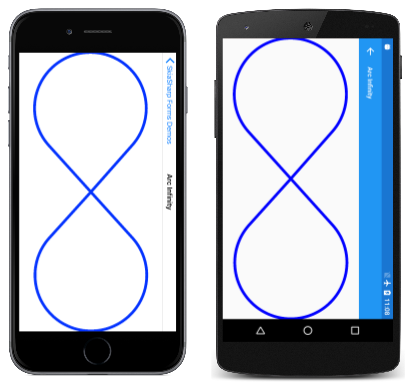
Per ottenere un adattamento più stretto, utilizzare la TightBounds proprietà , che esclude i punti di controllo. Ecco il programma in esecuzione in modalità orizzontale e la TightBounds proprietà per ottenere i limiti del percorso:

Anche se i collegamenti tra gli archi e le linee rette sono matematicamente smussati, il cambiamento dall'arco alla linea retta potrebbe sembrare un po 'improvviso. Un segno di infinito migliore è presentato nell'articolo successivo su Tre tipi di curve di Bézier.

Collegamenti correlati

• API SkiaSharp