series_fit_poly()
Si applica a: ✅Microsoft Fabric✅Azure Esplora dati✅ Azure Monitor✅Microsoft Sentinel
Applica una regressione polinomiale da una variabile indipendente (x_series) a una variabile dipendente (y_series). Questa funzione accetta una tabella contenente più serie (matrici numeriche dinamiche) e genera il polinomiale più adatto per ogni serie usando la regressione polinomiale.
Suggerimento
- Per la regressione lineare di una serie con spaziatura uniforme, come creato dall'operatore make-series, usare la funzione più semplice series_fit_line(). Vedere l'esempio 2.
- Se viene fornito x_series e la regressione viene eseguita per un livello elevato, prendere in considerazione la normalizzazione dell'intervallo [0-1]. Vedere l'esempio 3.
- Se x_series è di tipo datetime, deve essere convertito in double e normalizzato. Vedere l'esempio 3.
- Per l'implementazione di riferimento della regressione polinomiale con Python inline, vedere series_fit_poly_fl().
Sintassi
T | extend series_fit_poly( y_series [ , x_series , degree ])
Altre informazioni sulle convenzioni di sintassi.
Parametri
| Nome | Digita | Obbligatorio | Descrizione |
|---|---|---|---|
| y_series | dynamic |
✔️ | Matrice di valori numerici contenente la variabile dipendente. |
| x_series | dynamic |
Matrice di valori numerici contenente la variabile indipendente. Obbligatorio solo per le serie con spaziatura irregolare. Se non specificato, viene impostato su un valore predefinito [1, 2, ..., length(y_series)]. | |
| grado | Ordine richiesto del polinomio da adattare. Ad esempio, 1 per la regressione lineare, 2 per la regressione quadratica e così via. Il valore predefinito è 1, che indica la regressione lineare. |
Valori restituiti
La series_fit_poly() funzione restituisce le colonne seguenti:
rsquare: r-square è una misura standard della qualità dell'adattamento. Il valore è un numero nell'intervallo [0-1], dove 1 - è la scelta migliore possibile e 0 indica che i dati non sono ordinati e non rientrano in alcuna riga.coefficients: matrice numerica che contiene i coefficienti del polinomio più adatto al grado specificato, ordinato dal coefficiente di potenza più alto al più basso.variance: varianza della variabile dipendente (y_series).rvariance: varianza residua che corrisponde alla varianza tra i valori dei dati di input quelli approssimativi.poly_fit: matrice numerica che contiene una serie di valori del polinomio più adatto. La lunghezza della serie è uguale alla lunghezza della variabile dipendente (y_series). Valore utilizzato per la creazione di grafici.
Esempi
Esempio 1
Un polinomio di quinto ordine con rumore sugli assi x & y:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
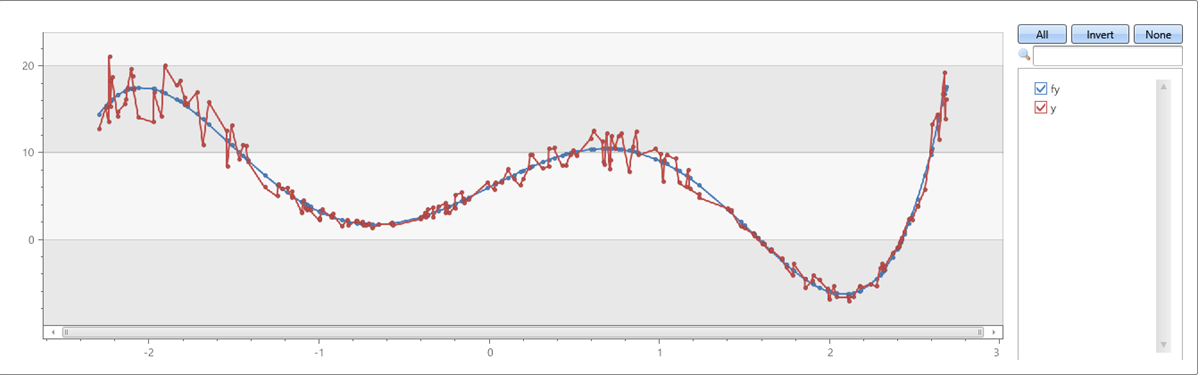
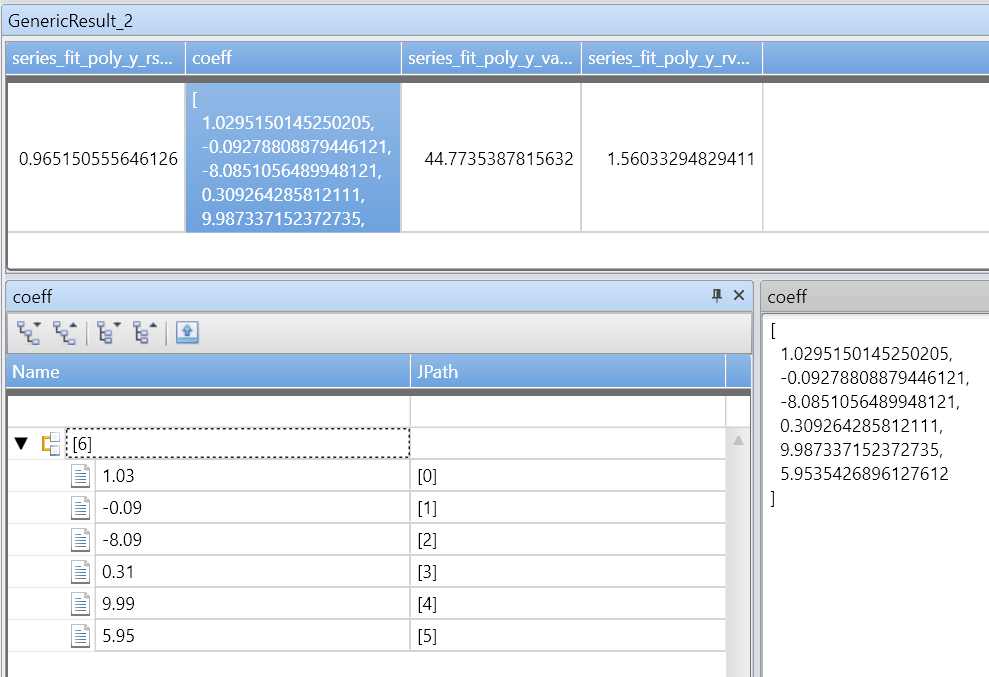
Esempio 2
Verificare che series_fit_poly con degree=1 corrisponda series_fit_linea :
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
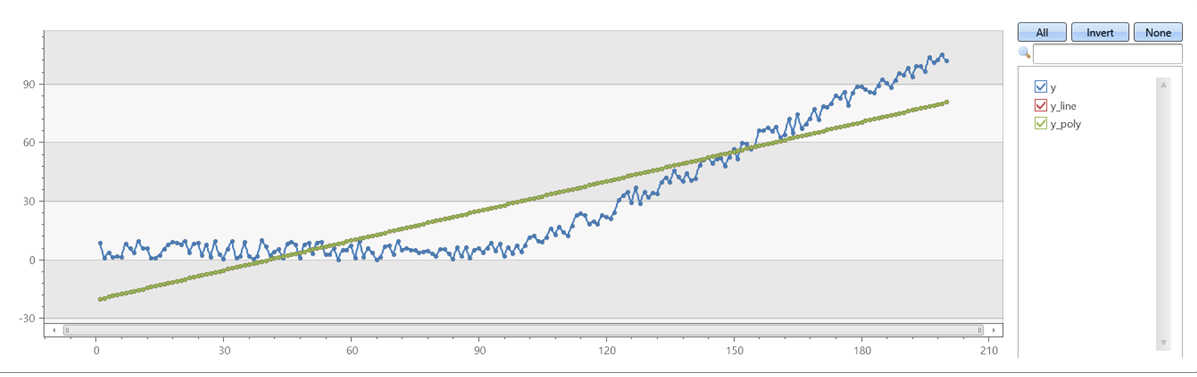

Esempio 3
Serie temporali irregolari (con spaziatura irregolare):
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
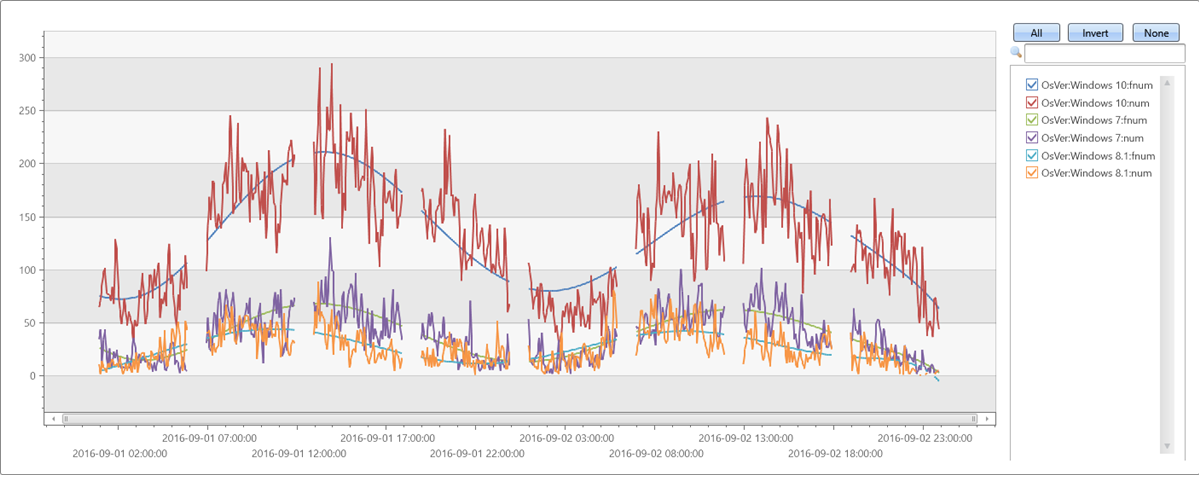
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)