Diversi modi per eseguire Lo strumento di stima delle risorse
Questo articolo illustra come usare Lo strumento di stima delle risorse di Azure Quantum. Lo strumento di stima delle risorse consente di stimare le risorse necessarie per eseguire un programma quantistico in un computer quantistico. È possibile usare Lo strumento di stima delle risorse per stimare il numero di qubit, il numero di cancelli e la profondità del circuito necessario per eseguire un programma quantistico.
Resource Estimator è disponibile in Visual Studio Code con l'estensione Quantum Development Kit. Per ulteriori informazioni, vedere Installare il Kit di Sviluppo Quantum.
Avvertimento
Lo strumento di stima delle risorse nel portale di Azure è deprecato. È consigliabile passare allo strumento di stima delle risorse locale in Visual Studio Code fornito in Quantum Development Kit.
Prerequisiti per VS Code
- La versione più recente di Visual Studio Code o aprire VS Code sul Web.
- La versione più recente della estensione del Quantum Development Kit. Per informazioni dettagliate sull'installazione, vedere Configurare l'estensione QDK.
Suggerimento
Non è necessario avere un account Azure per eseguire Lo strumento di stima delle risorse.
Creare un nuovo file Q#
- Aprire Visual Studio Code e selezionare File > Nuovo file di testo per creare un nuovo file.
- Salvare il file come
ShorRE.qs. Questo file conterrà il codice Q# per il programma.
Creare l'algoritmo quantistico
Copiare il codice seguente nel ShorRE.qs file :
import Std.Arrays.*;
import Std.Canon.*;
import Std.Convert.*;
import Std.Diagnostics.*;
import Std.Math.*;
import Std.Measurement.*;
import Microsoft.Quantum.Unstable.Arithmetic.*;
import Std.ResourceEstimation.*;
operation Main() : Unit {
let bitsize = 31;
// When choosing parameters for `EstimateFrequency`, make sure that
// generator and modules are not co-prime
let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize);
}
// In this sample we concentrate on costing the `EstimateFrequency`
// operation, which is the core quantum operation in Shors algorithm, and
// we omit the classical pre- and post-processing.
/// # Summary
/// Estimates the frequency of a generator
/// in the residue ring Z mod `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order (period)
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## bitsize
/// Number of bits needed to represent the modulus.
///
/// # Output
/// The numerator k of dyadic fraction k/2^bitsPrecision
/// approximating s/r.
operation EstimateFrequency(
generator : Int,
modulus : Int,
bitsize : Int
)
: Int {
mutable frequencyEstimate = 0;
let bitsPrecision = 2 * bitsize + 1;
// Allocate qubits for the superposition of eigenstates of
// the oracle that is used in period finding.
use eigenstateRegister = Qubit[bitsize];
// Initialize eigenstateRegister to 1, which is a superposition of
// the eigenstates we are estimating the phases of.
// We first interpret the register as encoding an unsigned integer
// in little endian encoding.
ApplyXorInPlace(1, eigenstateRegister);
let oracle = ApplyOrderFindingOracle(generator, modulus, _, _);
// Use phase estimation with a semiclassical Fourier transform to
// estimate the frequency.
use c = Qubit();
for idx in bitsPrecision - 1..-1..0 {
within {
H(c);
} apply {
// `BeginEstimateCaching` and `EndEstimateCaching` are the operations
// exposed by Azure Quantum Resource Estimator. These will instruct
// resource counting such that the if-block will be executed
// only once, its resources will be cached, and appended in
// every other iteration.
if BeginEstimateCaching("ControlledOracle", SingleVariant()) {
Controlled oracle([c], (1 <<< idx, eigenstateRegister));
EndEstimateCaching();
}
R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c);
}
if MResetZ(c) == One {
frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx);
}
}
// Return all the qubits used for oracles eigenstate back to 0 state
// using Microsoft.Quantum.Intrinsic.ResetAll.
ResetAll(eigenstateRegister);
return frequencyEstimate;
}
/// # Summary
/// Interprets `target` as encoding unsigned little-endian integer k
/// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where
/// p is `power`, g is `generator` and N is `modulus`.
///
/// # Input
/// ## generator
/// The unsigned integer multiplicative order ( period )
/// of which is being estimated. Must be co-prime to `modulus`.
/// ## modulus
/// The modulus which defines the residue ring Z mod `modulus`
/// in which the multiplicative order of `generator` is being estimated.
/// ## power
/// Power of `generator` by which `target` is multiplied.
/// ## target
/// Register interpreted as little endian encoded which is multiplied by
/// given power of the generator. The multiplication is performed modulo
/// `modulus`.
internal operation ApplyOrderFindingOracle(
generator : Int, modulus : Int, power : Int, target : Qubit[]
)
: Unit
is Adj + Ctl {
// The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We
// also use `ExpModI` to compute a by which x must be multiplied. Also
// note that we interpret target as unsigned integer in little-endian
// encoding.
ModularMultiplyByConstant(modulus,
ExpModI(generator, power, modulus),
target);
}
/// # Summary
/// Performs modular in-place multiplication by a classical constant.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(c*x) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular multiplication
/// ## c
/// Constant by which to multiply |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
use qs = Qubit[Length(y)];
for (idx, yq) in Enumerated(y) {
let shiftedC = (c <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, shiftedC, qs));
}
ApplyToEachCA(SWAP, Zipped(y, qs));
let invC = InverseModI(c, modulus);
for (idx, yq) in Enumerated(y) {
let shiftedC = (invC <<< idx) % modulus;
Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs));
}
}
/// # Summary
/// Performs modular in-place addition of a classical constant into a
/// quantum register.
///
/// # Description
/// Given the classical constants `c` and `modulus`, and an input
/// quantum register |𝑦⟩, this operation
/// computes `(x+c) % modulus` into |𝑦⟩.
///
/// # Input
/// ## modulus
/// Modulus to use for modular addition
/// ## c
/// Constant to add to |𝑦⟩
/// ## y
/// Quantum register of target
internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[])
: Unit is Adj + Ctl {
body (...) {
Controlled ModularAddConstant([], (modulus, c, y));
}
controlled (ctrls, ...) {
// We apply a custom strategy to control this operation instead of
// letting the compiler create the controlled variant for us in which
// the `Controlled` functor would be distributed over each operation
// in the body.
//
// Here we can use some scratch memory to save ensure that at most one
// control qubit is used for costly operations such as `AddConstant`
// and `CompareGreaterThenOrEqualConstant`.
if Length(ctrls) >= 2 {
use control = Qubit();
within {
Controlled X(ctrls, control);
} apply {
Controlled ModularAddConstant([control], (modulus, c, y));
}
} else {
use carry = Qubit();
Controlled AddConstant(ctrls, (c, y + [carry]));
Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry]));
Controlled AddConstant([carry], (modulus, y));
Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry));
}
}
}
/// # Summary
/// Performs in-place addition of a constant into a quantum register.
///
/// # Description
/// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive
/// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩.
///
/// # Input
/// ## c
/// Constant number to add to |𝑦⟩.
/// ## y
/// Quantum register of second summand and target; must not be empty.
internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl {
// We are using this version instead of the library version that is based
// on Fourier angles to show an advantage of sparse simulation in this sample.
let n = Length(y);
Fact(n > 0, "Bit width must be at least 1");
Fact(c >= 0, "constant must not be negative");
Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}");
if c != 0 {
// If c has j trailing zeroes than the j least significant bits
// of y won't be affected by the addition and can therefore be
// ignored by applying the addition only to the other qubits and
// shifting c accordingly.
let j = NTrailingZeroes(c);
use x = Qubit[n - j];
within {
ApplyXorInPlace(c >>> j, x);
} apply {
IncByLE(x, y[j...]);
}
}
}
/// # Summary
/// Performs greater-than-or-equals comparison to a constant.
///
/// # Description
/// Toggles output qubit `target` if and only if input register `x`
/// is greater than or equal to `c`.
///
/// # Input
/// ## c
/// Constant value for comparison.
/// ## x
/// Quantum register to compare against.
/// ## target
/// Target qubit for comparison result.
///
/// # Reference
/// This construction is described in [Lemma 3, arXiv:2201.10200]
internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit)
: Unit is Adj+Ctl {
let bitWidth = Length(x);
if c == 0 {
X(target);
} elif c >= 2 ^ bitWidth {
// do nothing
} elif c == 2 ^ (bitWidth - 1) {
ApplyLowTCNOT(Tail(x), target);
} else {
// normalize constant
let l = NTrailingZeroes(c);
let cNormalized = c >>> l;
let xNormalized = x[l...];
let bitWidthNormalized = Length(xNormalized);
let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized));
use qs = Qubit[bitWidthNormalized - 1];
let cs1 = [Head(xNormalized)] + Most(qs);
let cs2 = Rest(xNormalized);
within {
for i in IndexRange(gates) {
(gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]);
}
} apply {
ApplyLowTCNOT(Tail(qs), target);
}
}
}
/// # Summary
/// Internal operation used in the implementation of GreaterThanOrEqualConstant.
internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj {
within {
ApplyToEachA(X, [control1, control2]);
} apply {
ApplyAnd(control1, control2, target);
X(target);
}
}
internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit)
: Unit is Adj {
body (...) {
CCNOT(control1, control2, target);
}
adjoint (...) {
H(target);
if (M(target) == One) {
X(target);
CZ(control1, control2);
}
}
}
/// # Summary
/// Returns the number of trailing zeroes of a number
///
/// ## Example
/// ```qsharp
/// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0
/// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2
/// ```
internal function NTrailingZeroes(number : Int) : Int {
mutable nZeroes = 0;
mutable copy = number;
while (copy % 2 == 0) {
nZeroes += 1;
copy /= 2;
}
return nZeroes;
}
/// # Summary
/// An implementation for `CNOT` that when controlled using a single control uses
/// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7.
internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl {
body (...) {
CNOT(a, b);
}
adjoint self;
controlled (ctls, ...) {
// In this application this operation is used in a way that
// it is controlled by at most one qubit.
Fact(Length(ctls) <= 1, "At most one control line allowed");
if IsEmpty(ctls) {
CNOT(a, b);
} else {
use q = Qubit();
within {
ApplyAnd(Head(ctls), a, q);
} apply {
CNOT(q, b);
}
}
}
controlled adjoint self;
}
Eseguire lo strumento di stima delle risorse
Resource Estimator offre sei parametri qubit predefiniti, quattro dei quali hanno set di istruzioni basati su gate e due con un set di istruzioni Majorana. Offre anche due codici di correzione degli errori quantistici e surface_codefloquet_code.
In questo esempio si esegue l'oggetto Resource Estimator usando il qubit_gate_us_e3 parametro qubit e il surface_code codice di correzione degli errori quantistici.
Selezionare Visualizza -> Riquadro comandi e digitare "risorsa" che dovrebbe visualizzare l'opzione Q#: Calculate Resource Estimates (Calcola stime risorse). È anche possibile fare clic su Stima nell'elenco dei comandi visualizzati subito prima dell'operazione
Main. Selezionare questa opzione per aprire la finestra Stima risorse.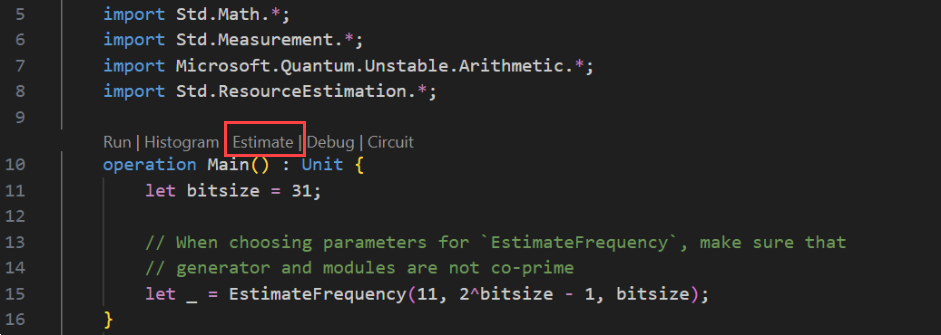
È possibile selezionare uno o più tipi di codice Qubit + Correzione errori per stimare le risorse. Per questo esempio, selezionare qubit_gate_us_e3 e fare clic su OK.
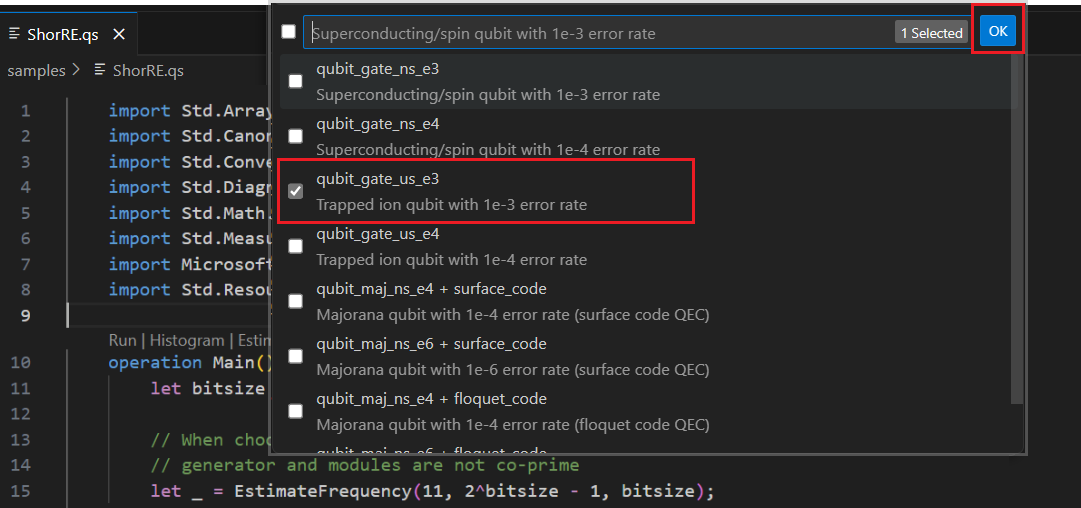
Specificare il budget degli errori o accettare il valore predefinito 0,001. Per questo esempio, lasciare il valore predefinito e premere INVIO.
Premere INVIO per accettare il nome del risultato predefinito in base al nome file, in questo caso ShorRE.
Visualizzare i risultati
Lo strumento di stima delle risorse fornisce più stime per lo stesso algoritmo, ognuna delle quali mostra i compromessi tra il numero di qubit e il runtime. Comprendere il compromesso tra runtime e scalabilità di sistema è uno degli aspetti più importanti della stima delle risorse.
Il risultato della stima delle risorse viene visualizzato nella finestra Stima Q#.
Nella scheda Risultati viene visualizzato un riepilogo della stima delle risorse. Fare clic sull'icona accanto alla prima riga per selezionare le colonne da visualizzare. È possibile scegliere tra nome di esecuzione, tipo di stima, tipo di qubit, schema qec, budget degli errori, qubit logici, profondità logica, distanza del codice, stati T, T factory, frazione di T factory, runtime, rQOPS e qubit fisici.
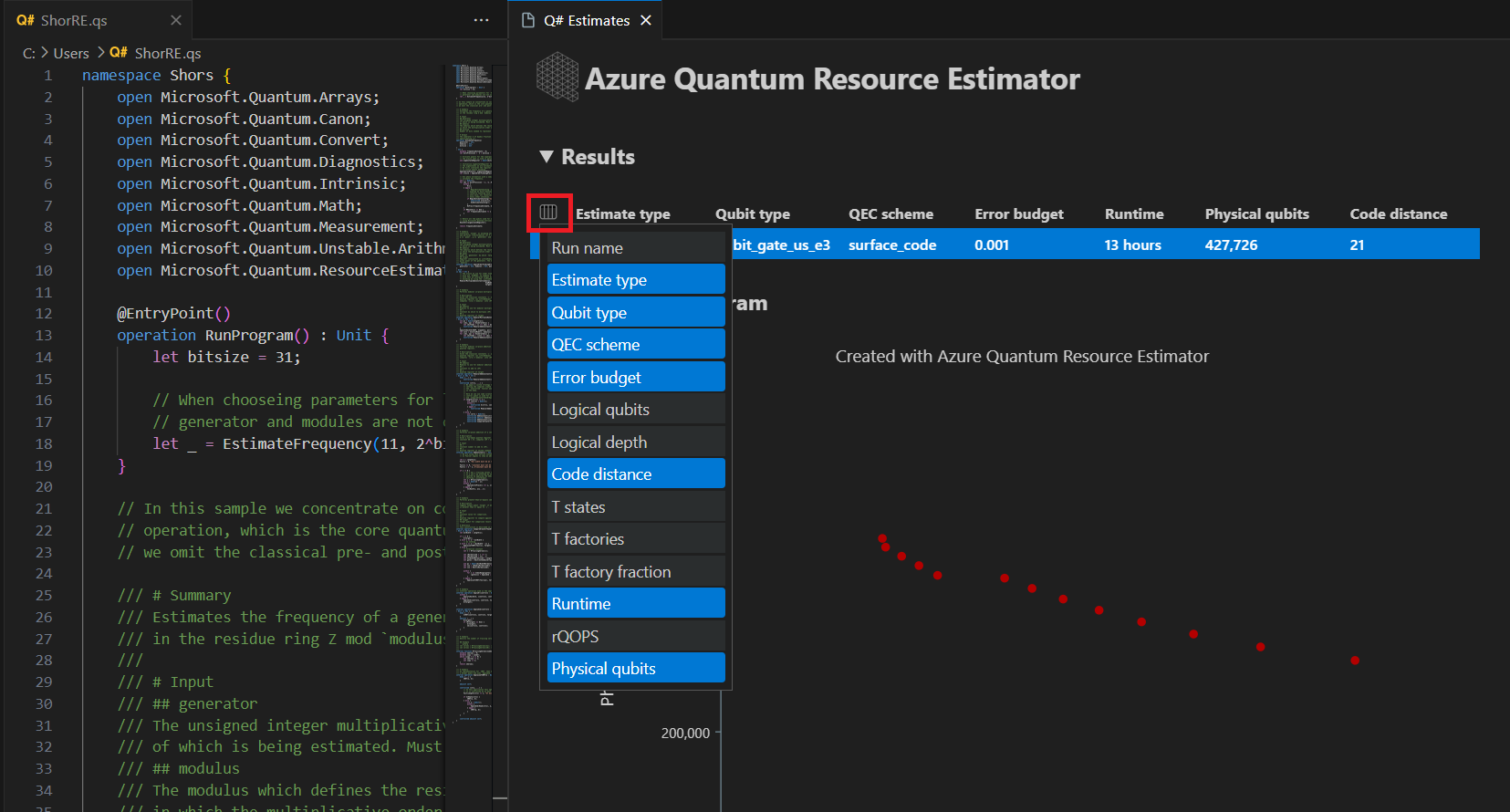
Nella colonna Tipo di stima della tabella dei risultati è possibile visualizzare il numero di combinazioni ottimali di {numero di qubit, runtime} per l'algoritmo. Queste combinazioni possono essere visualizzate nel diagramma dello spazio-tempo.
Il diagramma spazio-tempo mostra i compromessi tra il numero di qubit fisici e il runtime dell'algoritmo. In questo caso, lo strumento di stima delle risorse trova 13 diverse combinazioni ottimali su molte migliaia di possibili. È possibile passare il puntatore del mouse su ogni {numero di qubit, runtime} per visualizzare i dettagli della stima delle risorse in quel punto.
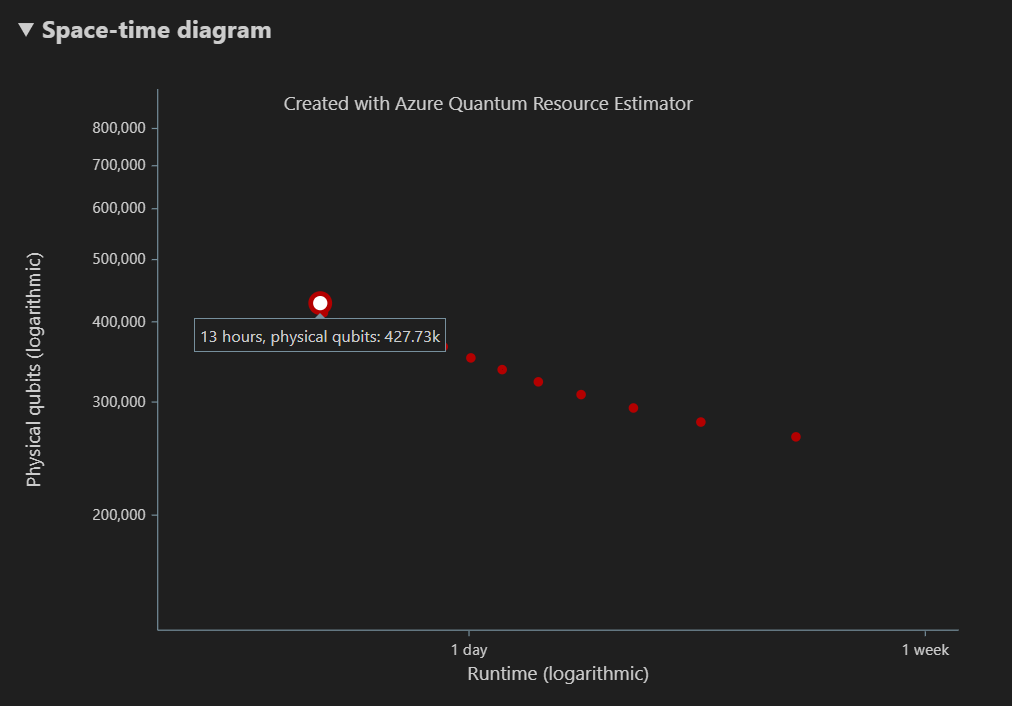
Per altre informazioni, vedere Diagramma spazio-tempo.
Nota
È necessario fare clic su un punto del diagramma spaziale, ovvero una coppia {numero di qubit, runtime} per visualizzare il diagramma spaziale e i dettagli della stima delle risorse corrispondente a tale punto.
Il diagramma spaziale mostra la distribuzione dei qubit fisici usati per l'algoritmo e le factory T, corrispondenti a una coppia {numero di qubit, runtime}. Ad esempio, se si seleziona il punto più a sinistra nel diagramma dello spazio-tempo, il numero di qubit fisici necessari per eseguire l'algoritmo è 427726, 196686 di cui sono qubit di algoritmo e 231040 di cui sono qubit di T factory.
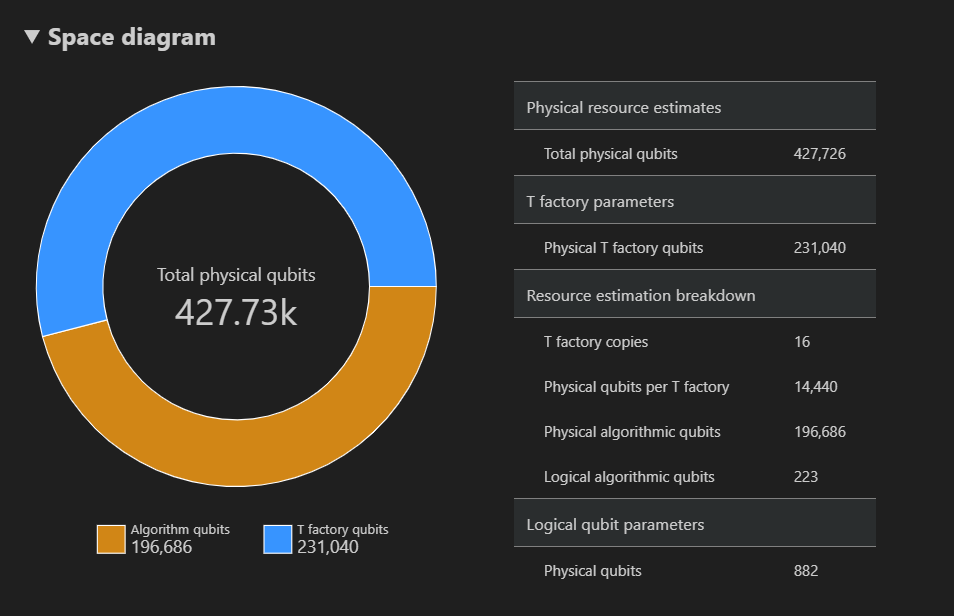
Infine, nella scheda Stime risorse viene visualizzato l'elenco completo dei dati di output per l'oggetto Resource Estimator corrispondente a una coppia di {numero di qubit, runtime} . È possibile controllare i dettagli dei costi comprimendo i gruppi, che includono altre informazioni. Ad esempio, selezionare il punto più a sinistra nel diagramma spazio-tempo e comprimere il gruppo di parametri qubit logici .
Parametro qubit logico Valore Schema Correzione degli errori quantistici surface_code Distanza di codice 21 Qubit fisici 882 Tempo ciclo logico 13 millisecs Frequenza di errore del qubit logico 3.00E-13 Attraversamento del prefactoring 0.03 Soglia di correzione degli errori 0,01 Formula tempo del ciclo logico (4 * twoQubitGateTime+ 2 *oneQubitMeasurementTime) *codeDistanceFormula qubit fisici 2 * codeDistance*codeDistanceSuggerimento
Fare clic su Mostra righe dettagliate per visualizzare la descrizione di ogni output dei dati del report.
Per altre informazioni, vedere i dati completi del report di Resource Estimator.
Modificare i target parametri
È possibile stimare il costo per lo stesso programma Q# usando altri tipi di qubit, codice di correzione degli errori e budget degli errori. Aprire la finestra Stima risorse selezionando Visualizza -> Riquadro comandi e digitare Q#: Calculate Resource Estimates.
Selezionare qualsiasi altra configurazione, ad esempio il parametro qubit basato su Majorana, qubit_maj_ns_e6. Accettare il valore predefinito del budget degli errori o immetterne uno nuovo e premere INVIO. Lo strumento di stima delle risorse esegue nuovamente la stima con i nuovi target parametri.
Per altre informazioni, vedere Target parametri per Lo strumento di stima delle risorse.
Eseguire più configurazioni di parametri
Azure Quantum Resource Estimator può eseguire più configurazioni di target parametri e confrontare i risultati della stima delle risorse.
Selezionare Visualizza -> Riquadro comandi oppure premere CTRL+MAIUSC+P e digitare
Q#: Calculate Resource Estimates.Selezionare qubit_gate_us_e3, qubit_gate_us_e4, qubit_maj_ns_e4 + floquet_code e qubit_maj_ns_e6 + floquet_code e fare clic su OK.
Accettare il valore predefinito del budget di errore 0,001 e premere INVIO.
Premere INVIO per accettare il file di input, in questo caso ShorRE.qs.
Nel caso di più configurazioni di parametri, i risultati vengono visualizzati in righe diverse nella scheda Risultati .
Il diagramma Spazio-tempo mostra i risultati per tutte le configurazioni dei parametri. La prima colonna della tabella dei risultati visualizza la legenda per ogni configurazione dei parametri. È possibile passare il puntatore del mouse su ogni punto per visualizzare i dettagli della stima delle risorse in quel punto.
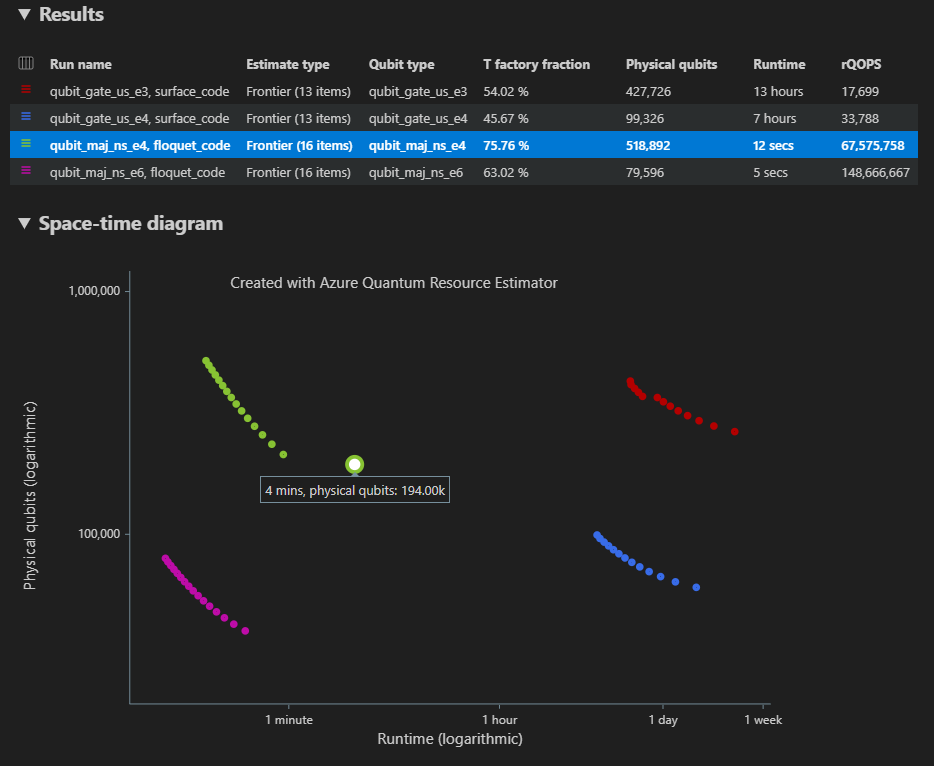
Fare clic su un punto {number of qubits, runtime} (Numero di qubit, runtime) del diagramma spazio-tempo per visualizzare i dati corrispondenti del diagramma spaziale e del report.
Prerequisiti per Jupyter Notebook in VS Code
Un ambiente Python con Python e Pip installati.
La versione più recente di Visual Studio Code o aprire VS Code sul Web.
VS Code con Quantum Development Kit, Pythone estensioni di Jupyter installate.
I pacchetti e
qsharpAzure Quantumqsharp_widgetspiù recenti.python -m pip install --upgrade qsharp qsharp_widgetso
!pip install --upgrade qsharp qsharp_widgets
Suggerimento
Non è necessario avere un account Azure per eseguire Lo strumento di stima delle risorse.
Creare l'algoritmo quantistico
In VS Code, selezionare Visualizza > Riquadro comandi e selezionare Crea: Nuovo Jupyter Notebook.
In alto a destra VS Code rileverà e visualizzerà la versione di Python e l'ambiente Python virtuale selezionato per il notebook. Se si dispone di più ambienti Python, potrebbe essere necessario selezionare un kernel usando la selezione kernel in alto a destra. Se non è stato rilevato alcun ambiente, vedere Jupyter Notebooks in VS Code per informazioni sull'installazione.
Nella prima cella del notebook importare il pacchetto
qsharp.import qsharpAggiungere una nuova cella e copiare il codice seguente.
%%qsharp import Std.Arrays.*; import Std.Canon.*; import Std.Convert.*; import Std.Diagnostics.*; import Std.Math.*; import Std.Measurement.*; import Microsoft.Quantum.Unstable.Arithmetic.*; import Std.ResourceEstimation.*; operation RunProgram() : Unit { let bitsize = 31; // When choosing parameters for `EstimateFrequency`, make sure that // generator and modules are not co-prime let _ = EstimateFrequency(11, 2^bitsize - 1, bitsize); } // In this sample we concentrate on costing the `EstimateFrequency` // operation, which is the core quantum operation in Shors algorithm, and // we omit the classical pre- and post-processing. /// # Summary /// Estimates the frequency of a generator /// in the residue ring Z mod `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order (period) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## bitsize /// Number of bits needed to represent the modulus. /// /// # Output /// The numerator k of dyadic fraction k/2^bitsPrecision /// approximating s/r. operation EstimateFrequency( generator : Int, modulus : Int, bitsize : Int ) : Int { mutable frequencyEstimate = 0; let bitsPrecision = 2 * bitsize + 1; // Allocate qubits for the superposition of eigenstates of // the oracle that is used in period finding. use eigenstateRegister = Qubit[bitsize]; // Initialize eigenstateRegister to 1, which is a superposition of // the eigenstates we are estimating the phases of. // We first interpret the register as encoding an unsigned integer // in little endian encoding. ApplyXorInPlace(1, eigenstateRegister); let oracle = ApplyOrderFindingOracle(generator, modulus, _, _); // Use phase estimation with a semiclassical Fourier transform to // estimate the frequency. use c = Qubit(); for idx in bitsPrecision - 1..-1..0 { within { H(c); } apply { // `BeginEstimateCaching` and `EndEstimateCaching` are the operations // exposed by Azure Quantum Resource Estimator. These will instruct // resource counting such that the if-block will be executed // only once, its resources will be cached, and appended in // every other iteration. if BeginEstimateCaching("ControlledOracle", SingleVariant()) { Controlled oracle([c], (1 <<< idx, eigenstateRegister)); EndEstimateCaching(); } R1Frac(frequencyEstimate, bitsPrecision - 1 - idx, c); } if MResetZ(c) == One { frequencyEstimate += 1 <<< (bitsPrecision - 1 - idx); } } // Return all the qubits used for oracle eigenstate back to 0 state // using Microsoft.Quantum.Intrinsic.ResetAll. ResetAll(eigenstateRegister); return frequencyEstimate; } /// # Summary /// Interprets `target` as encoding unsigned little-endian integer k /// and performs transformation |k⟩ ↦ |gᵖ⋅k mod N ⟩ where /// p is `power`, g is `generator` and N is `modulus`. /// /// # Input /// ## generator /// The unsigned integer multiplicative order ( period ) /// of which is being estimated. Must be co-prime to `modulus`. /// ## modulus /// The modulus which defines the residue ring Z mod `modulus` /// in which the multiplicative order of `generator` is being estimated. /// ## power /// Power of `generator` by which `target` is multiplied. /// ## target /// Register interpreted as little endian encoded which is multiplied by /// given power of the generator. The multiplication is performed modulo /// `modulus`. internal operation ApplyOrderFindingOracle( generator : Int, modulus : Int, power : Int, target : Qubit[] ) : Unit is Adj + Ctl { // The oracle we use for order finding implements |x⟩ ↦ |x⋅a mod N⟩. We // also use `ExpModI` to compute a by which x must be multiplied. Also // note that we interpret target as unsigned integer in little-endian // encoding. ModularMultiplyByConstant(modulus, ExpModI(generator, power, modulus), target); } /// # Summary /// Performs modular in-place multiplication by a classical constant. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(c*x) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular multiplication /// ## c /// Constant by which to multiply |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularMultiplyByConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { use qs = Qubit[Length(y)]; for (idx, yq) in Enumerated(y) { let shiftedC = (c <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, shiftedC, qs)); } ApplyToEachCA(SWAP, Zipped(y, qs)); let invC = InverseModI(c, modulus); for (idx, yq) in Enumerated(y) { let shiftedC = (invC <<< idx) % modulus; Controlled ModularAddConstant([yq], (modulus, modulus - shiftedC, qs)); } } /// # Summary /// Performs modular in-place addition of a classical constant into a /// quantum register. /// /// # Description /// Given the classical constants `c` and `modulus`, and an input /// quantum register |𝑦⟩, this operation /// computes `(x+c) % modulus` into |𝑦⟩. /// /// # Input /// ## modulus /// Modulus to use for modular addition /// ## c /// Constant to add to |𝑦⟩ /// ## y /// Quantum register of target internal operation ModularAddConstant(modulus : Int, c : Int, y : Qubit[]) : Unit is Adj + Ctl { body (...) { Controlled ModularAddConstant([], (modulus, c, y)); } controlled (ctrls, ...) { // We apply a custom strategy to control this operation instead of // letting the compiler create the controlled variant for us in which // the `Controlled` functor would be distributed over each operation // in the body. // // Here we can use some scratch memory to save ensure that at most one // control qubit is used for costly operations such as `AddConstant` // and `CompareGreaterThenOrEqualConstant`. if Length(ctrls) >= 2 { use control = Qubit(); within { Controlled X(ctrls, control); } apply { Controlled ModularAddConstant([control], (modulus, c, y)); } } else { use carry = Qubit(); Controlled AddConstant(ctrls, (c, y + [carry])); Controlled Adjoint AddConstant(ctrls, (modulus, y + [carry])); Controlled AddConstant([carry], (modulus, y)); Controlled CompareGreaterThanOrEqualConstant(ctrls, (c, y, carry)); } } } /// # Summary /// Performs in-place addition of a constant into a quantum register. /// /// # Description /// Given a non-empty quantum register |𝑦⟩ of length 𝑛+1 and a positive /// constant 𝑐 < 2ⁿ, computes |𝑦 + c⟩ into |𝑦⟩. /// /// # Input /// ## c /// Constant number to add to |𝑦⟩. /// ## y /// Quantum register of second summand and target; must not be empty. internal operation AddConstant(c : Int, y : Qubit[]) : Unit is Adj + Ctl { // We are using this version instead of the library version that is based // on Fourier angles to show an advantage of sparse simulation in this sample. let n = Length(y); Fact(n > 0, "Bit width must be at least 1"); Fact(c >= 0, "constant must not be negative"); Fact(c < 2 ^ n, $"constant must be smaller than {2L ^ n}"); if c != 0 { // If c has j trailing zeroes than the j least significant bits // of y will not be affected by the addition and can therefore be // ignored by applying the addition only to the other qubits and // shifting c accordingly. let j = NTrailingZeroes(c); use x = Qubit[n - j]; within { ApplyXorInPlace(c >>> j, x); } apply { IncByLE(x, y[j...]); } } } /// # Summary /// Performs greater-than-or-equals comparison to a constant. /// /// # Description /// Toggles output qubit `target` if and only if input register `x` /// is greater than or equal to `c`. /// /// # Input /// ## c /// Constant value for comparison. /// ## x /// Quantum register to compare against. /// ## target /// Target qubit for comparison result. /// /// # Reference /// This construction is described in [Lemma 3, arXiv:2201.10200] internal operation CompareGreaterThanOrEqualConstant(c : Int, x : Qubit[], target : Qubit) : Unit is Adj+Ctl { let bitWidth = Length(x); if c == 0 { X(target); } elif c >= 2 ^ bitWidth { // do nothing } elif c == 2 ^ (bitWidth - 1) { ApplyLowTCNOT(Tail(x), target); } else { // normalize constant let l = NTrailingZeroes(c); let cNormalized = c >>> l; let xNormalized = x[l...]; let bitWidthNormalized = Length(xNormalized); let gates = Rest(IntAsBoolArray(cNormalized, bitWidthNormalized)); use qs = Qubit[bitWidthNormalized - 1]; let cs1 = [Head(xNormalized)] + Most(qs); let cs2 = Rest(xNormalized); within { for i in IndexRange(gates) { (gates[i] ? ApplyAnd | ApplyOr)(cs1[i], cs2[i], qs[i]); } } apply { ApplyLowTCNOT(Tail(qs), target); } } } /// # Summary /// Internal operation used in the implementation of GreaterThanOrEqualConstant. internal operation ApplyOr(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { within { ApplyToEachA(X, [control1, control2]); } apply { ApplyAnd(control1, control2, target); X(target); } } internal operation ApplyAnd(control1 : Qubit, control2 : Qubit, target : Qubit) : Unit is Adj { body (...) { CCNOT(control1, control2, target); } adjoint (...) { H(target); if (M(target) == One) { X(target); CZ(control1, control2); } } } /// # Summary /// Returns the number of trailing zeroes of a number /// /// ## Example /// ```qsharp /// let zeroes = NTrailingZeroes(21); // = NTrailingZeroes(0b1101) = 0 /// let zeroes = NTrailingZeroes(20); // = NTrailingZeroes(0b1100) = 2 /// ``` internal function NTrailingZeroes(number : Int) : Int { mutable nZeroes = 0; mutable copy = number; while (copy % 2 == 0) { nZeroes += 1; copy /= 2; } return nZeroes; } /// # Summary /// An implementation for `CNOT` that when controlled using a single control uses /// a helper qubit and uses `ApplyAnd` to reduce the T-count to 4 instead of 7. internal operation ApplyLowTCNOT(a : Qubit, b : Qubit) : Unit is Adj+Ctl { body (...) { CNOT(a, b); } adjoint self; controlled (ctls, ...) { // In this application this operation is used in a way that // it is controlled by at most one qubit. Fact(Length(ctls) <= 1, "At most one control line allowed"); if IsEmpty(ctls) { CNOT(a, b); } else { use q = Qubit(); within { ApplyAnd(Head(ctls), a, q); } apply { CNOT(q, b); } } } controlled adjoint self; }
Stimare l'algoritmo quantistico
Stimare ora le risorse fisiche per l'operazione RunProgram usando i presupposti predefiniti. Aggiungere una nuova cella e copiare il codice seguente.
result = qsharp.estimate("RunProgram()")
result
La funzione qsharp.estimate crea un oggetto risultato, che può essere usato per visualizzare una tabella con il conto complessivo delle risorse fisiche. È possibile esaminare i dettagli dei costi espandendo i gruppi che contengono altre informazioni. Per altre informazioni, vedere i dati completi del report di Resource Estimator.
Ad esempio, espandi il gruppo dei parametri qubit logici per verificare che la distanza del codice sia 21 e il numero di qubit fisici sia 882.
| Parametro qubit logico | Valore |
|---|---|
| Schema Correzione degli errori quantistici | surface_code |
| Distanza di codice | 21 |
| Qubit fisici | 882 |
| Tempo ciclo logico | 8 millisecs |
| Frequenza di errore del qubit logico | 3.00E-13 |
| Attraversamento del prefactoring | 0.03 |
| Soglia di correzione degli errori | 0,01 |
| Formula tempo del ciclo logico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formula qubit fisici | 2 * codeDistance * codeDistance |
Suggerimento
Per una versione più compatta della tabella di output, è possibile usare result.summary.
Diagramma spaziale
La distribuzione dei qubit fisici usati per l'algoritmo e le factory T è un fattore che può influire sulla progettazione dell'algoritmo. È possibile usare il pacchetto qsharp-widgets per visualizzare questa distribuzione per comprendere meglio i requisiti di spazio stimati per l'algoritmo.
from qsharp-widgets import SpaceChart, EstimateDetails
SpaceChart(result)
In questo esempio, il numero di qubit fisici necessari per eseguire l'algoritmo è 829766, di cui 196686 sono qubit di algoritmo e 633080 sono qubit di T factory.
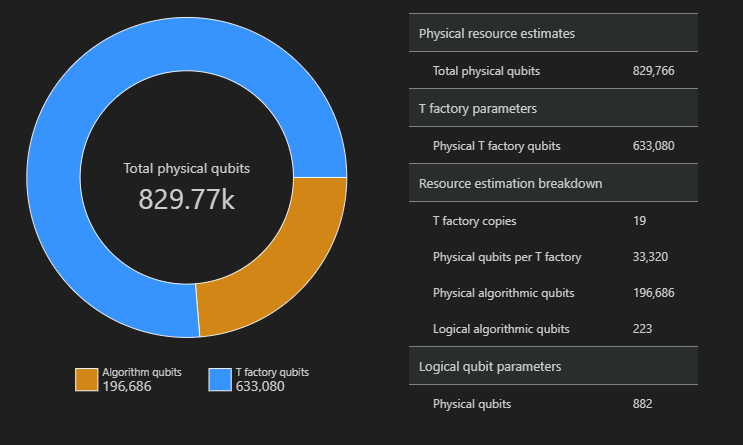
Modificare i valori predefiniti e stimare l'algoritmo
Quando si invia una richiesta di stima delle risorse per il programma, è possibile specificare alcuni parametri facoltativi. Usare il jobParams campo per accedere a tutti i target parametri che possono essere passati all'esecuzione del processo e verificare quali valori predefiniti sono stati presupposti:
result['jobParams']
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
È possibile notare che l'oggetto Strumento di stima delle risorse accetta il modello qubit qubit_gate_ns_e3, il codice di correzione degli errori surface_code e il budget degli errori 0,001 come valori predefiniti per la stima.
Questi sono i target parametri che è possibile personalizzare:
-
errorBudget: il budget complessivo degli errori consentito per l'algoritmo -
qecScheme: schema di correzione degli errori quantistici (QEC) -
qubitParams: parametri qubit fisici -
constraints: i vincoli a livello di componente -
distillationUnitSpecifications: le specifiche per gli algoritmi di crittografia delle factory T -
estimateType: singola o frontiera
Per altre informazioni, vedere Target parametri per Lo strumento di stima delle risorse.
Modificare il modello qubit
È possibile stimare il costo per lo stesso algoritmo usando il parametro qubit basato su Majorana, qubitParams, "qubit_maj_ns_e6".
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
}})
EstimateDetails(result_maj)
Modificare lo schema di correzione degli errori quantistici
È possibile rieseguire il processo di stima delle risorse per lo stesso esempio nei parametri qubit basati su Majorana con uno schema QEC floqued, qecScheme.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
}})
EstimateDetails(result_maj)
Modificare il budget degli errori
Eseguire quindi di nuovo lo stesso circuito quantistico con un valore errorBudget pari al 10%.
result_maj = qsharp.estimate("RunProgram()", params={
"qubitParams": {
"name": "qubit_maj_ns_e6"
},
"qecScheme": {
"name": "floquet_code"
},
"errorBudget": 0.1})
EstimateDetails(result_maj)
Invio in batch con lo strumento di stima delle risorse
Azure Quantum Resource Estimator consente di eseguire più configurazioni di target parametri e confrontare i risultati. Ciò è utile quando si vuole confrontare il costo di modelli qubit diversi, schemi QEC o budget di errore.
È possibile eseguire una stima batch passando un elenco di target parametri al
paramsparametro dellaqsharp.estimatefunzione. Ad esempio, eseguire lo stesso algoritmo con i parametri predefiniti e i parametri qubit basati su Majorana con uno schema QEC floquet.result_batch = qsharp.estimate("RunProgram()", params= [{}, # Default parameters { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" } }]) result_batch.summary_data_frame(labels=["Gate-based ns, 10⁻³", "Majorana ns, 10⁻⁶"])Modello Qubit logici Profondità logica T states Distanza di codice T factory Frazione T factory Qubit fisici rQOPS Runtime fisico Basato su gate ns 10⁻³ 223 3,64 M 4.70M 21 19 76.30 % 829.77k 26,55 M 31 sec Majorana ns 10⁻⁶ 223 3,64 M 4.70M 5 19 63.02 % 79.60k 148.67M 5 sec È anche possibile costruire un elenco di parametri di stima usando la
EstimatorParamsclasse .from qsharp.estimator import EstimatorParams, QubitParams, QECScheme, LogicalCounts labels = ["Gate-based µs, 10⁻³", "Gate-based µs, 10⁻⁴", "Gate-based ns, 10⁻³", "Gate-based ns, 10⁻⁴", "Majorana ns, 10⁻⁴", "Majorana ns, 10⁻⁶"] params = EstimatorParams(num_items=6) params.error_budget = 0.333 params.items[0].qubit_params.name = QubitParams.GATE_US_E3 params.items[1].qubit_params.name = QubitParams.GATE_US_E4 params.items[2].qubit_params.name = QubitParams.GATE_NS_E3 params.items[3].qubit_params.name = QubitParams.GATE_NS_E4 params.items[4].qubit_params.name = QubitParams.MAJ_NS_E4 params.items[4].qec_scheme.name = QECScheme.FLOQUET_CODE params.items[5].qubit_params.name = QubitParams.MAJ_NS_E6 params.items[5].qec_scheme.name = QECScheme.FLOQUET_CODEqsharp.estimate("RunProgram()", params=params).summary_data_frame(labels=labels)Modello Qubit logici Profondità logica T states Distanza di codice T factory Frazione T factory Qubit fisici rQOPS Runtime fisico Basato su gate µs 10⁻³ 223 3,64M 4.70M 17 13 40.54 % 216.77k 21,86 k 10 ore Basato su gate µs 10⁻⁴ 223 3,64 M 4.70M 9 14 43.17 % 63,57 k 41.30k 5 ore Basato su gate ns 10⁻³ 223 3,64M 4.70M 17 16 69.08 % 416.89k 32,79M 25 sec Basato su gate ns 10⁻⁴ 223 3,64M 4.70M 9 14 43.17 % 63,57 k 61,94M 13 sec Majorana ns 10⁻⁴ 223 3,64M 4.70M 9 19 82.75 % 501.48k 82.59M 10 sec Majorana ns 10⁻⁶ 223 3,64M 4.70M 5 13 31.47 % 42.96k 148.67M 5 sec
Esecuzione della stima della frontiera Pareto
Quando si stimano le risorse di un algoritmo, è importante considerare il compromesso tra il numero di qubit fisici e il runtime dell'algoritmo. È possibile considerare l'allocazione del maggior numero possibile di qubit fisici per ridurre il runtime dell'algoritmo. Tuttavia, il numero di qubit fisici è limitato dal numero di qubit fisici disponibili nell'hardware quantistico.
La stima della frontiera Pareto fornisce più stime per lo stesso algoritmo, ognuna con un compromesso tra il numero di qubit e il runtime.
Per eseguire Lo strumento di stima delle risorse usando la stima della frontiera Pareto, è necessario specificare il
"estimateType"target parametro come"frontier". Ad esempio, eseguire lo stesso algoritmo con i parametri qubit basati su Majorana con un codice di superficie usando la stima della frontiera Pareto.result = qsharp.estimate("RunProgram()", params= {"qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # frontier estimation } )È possibile usare la
EstimatesOverviewfunzione per visualizzare una tabella con i conteggi complessivi delle risorse fisiche. Fare clic sull'icona accanto alla prima riga per selezionare le colonne da visualizzare. È possibile scegliere tra nome di esecuzione, tipo di stima, tipo di qubit, schema qec, budget degli errori, qubit logici, profondità logica, distanza del codice, stati T, T factory, frazione di T factory, runtime, rQOPS e qubit fisici.from qsharp_widgets import EstimatesOverview EstimatesOverview(result)
Nella colonna Tipo di stima della tabella dei risultati è possibile visualizzare il numero di combinazioni diverse di {numero di qubit, runtime} per l'algoritmo. In questo caso, Lo strumento di stima delle risorse trova 22 combinazioni ottimali diverse tra molte migliaia di possibili.
Diagramma spazio-tempo
La EstimatesOverview funzione visualizza anche il diagramma spazio-tempo di Stima risorse.
Il diagramma dello spazio-tempo mostra il numero di qubit fisici e il runtime dell'algoritmo per ogni coppia {numero di qubit, runtime}. È possibile passare il puntatore del mouse su ogni punto per visualizzare i dettagli della stima delle risorse in quel punto.
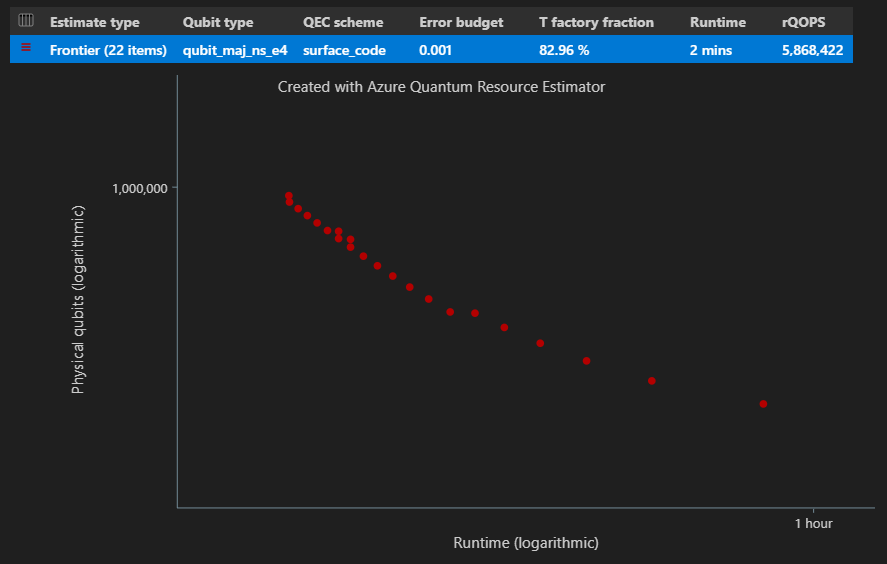
Invio in batch con stima della frontiera Pareto
Per stimare e confrontare più configurazioni di target parametri con la stima della frontiera, aggiungere
"estimateType": "frontier",ai parametri .result = qsharp.estimate( "RunProgram()", [ { "qubitParams": { "name": "qubit_maj_ns_e4" }, "qecScheme": { "name": "surface_code" }, "estimateType": "frontier", # Pareto frontier estimation }, { "qubitParams": { "name": "qubit_maj_ns_e6" }, "qecScheme": { "name": "floquet_code" }, "estimateType": "frontier", # Pareto frontier estimation }, ] ) EstimatesOverview(result, colors=["#1f77b4", "#ff7f0e"], runNames=["e4 Surface Code", "e6 Floquet Code"])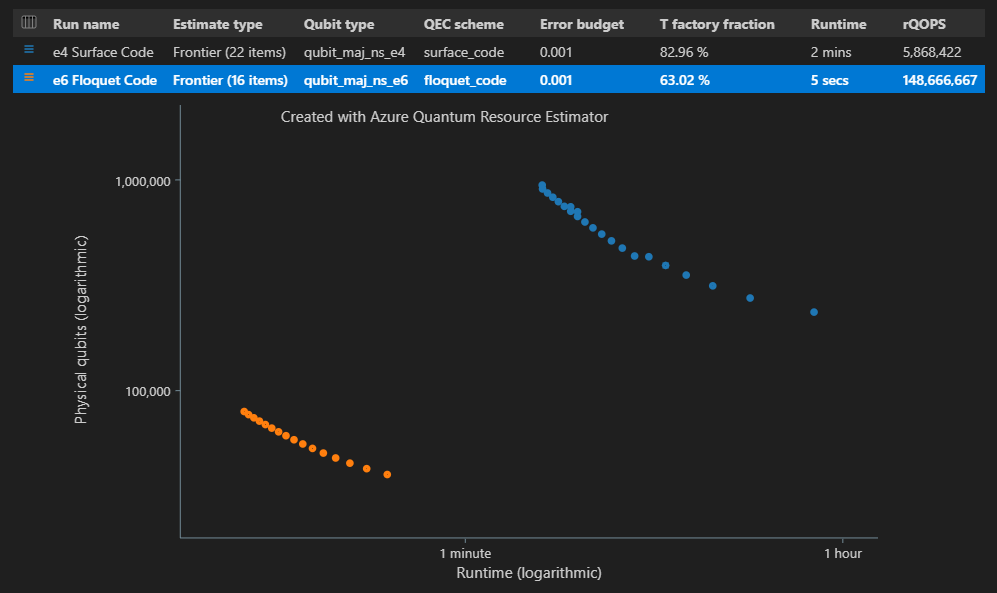
Nota
È possibile definire i colori ed eseguire i nomi per il diagramma di qubit-time usando la
EstimatesOverviewfunzione .Quando si eseguono più configurazioni di target parametri usando la stima della frontiera Pareto, è possibile visualizzare le stime delle risorse per un punto specifico del diagramma dello spazio-tempo, vale a dire per ogni coppia {numero di qubit, runtime}. Ad esempio, il codice seguente mostra l'utilizzo dei dettagli della stima per la seconda esecuzione (stima index=0) e il quarto runtime (indice punto=3) più breve.
EstimateDetails(result[1], 4)È anche possibile visualizzare il diagramma spaziale per un punto specifico del diagramma dello spazio-tempo. Ad esempio, il codice seguente mostra il diagramma spaziale per la prima esecuzione di combinazioni (stima index=0) e il terzo runtime più breve (indice punto=2).
SpaceChart(result[0], 2)
Prerequisiti per Qiskit in VS Code
Un ambiente Python con Python e Pip installati.
La versione più recente di Visual Studio Code o apri Visual Studio Code sul Web.
VS Code con Quantum Development Kit, Pythone estensioni di Jupyter installate.
Pacchetti di
qsharpeqsharp_widgetse diqiskitdi Azure Quantum più recenti.python -m pip install --upgrade qsharp qsharp_widgets qiskito
!pip install --upgrade qsharp qsharp_widgets qiskit
Suggerimento
Non è necessario avere un account Azure per eseguire Lo strumento di stima delle risorse.
Creare un nuovo notebook di Jupyter
- In VS Code, selezionare Visualizza > Riquadro comandi e selezionare Crea: Nuovo Jupyter Notebook.
- In alto a destra VS Code rileverà e visualizzerà la versione di Python e l'ambiente Python virtuale selezionato per il notebook. Se si dispone di più ambienti Python, potrebbe essere necessario selezionare un kernel usando la selezione kernel in alto a destra. Se non è stato rilevato alcun ambiente, vedere Jupyter Notebooks in VS Code per informazioni sull'installazione.
Creare l'algoritmo quantistico
In questo esempio viene creato un circuito quantistico per un moltiplicatore in base alla costruzione presentata in Conversion-Perez e Garcia-Escartin (arXiv:1411.5949) che usa la trasformazione Quantum Fourier per implementare l'aritmetica.
È possibile modificare le dimensioni del moltiplicatore modificando la bitwidth variabile. La generazione del circuito viene sottoposta a wrapping in una funzione che può essere chiamata con il bitwidth valore del moltiplicatore. L'operazione avrà due registri di input, ognuna delle dimensioni dell'oggetto specificato bitwidthe un registro di output che corrisponde al doppio delle dimensioni dell'oggetto specificato bitwidth. La funzione stampa anche alcuni conteggi delle risorse logiche per il moltiplicatore estratto direttamente dal circuito quantistico.
from qiskit.circuit.library import RGQFTMultiplier
def create_algorithm(bitwidth):
print(f"[INFO] Create a QFT-based multiplier with bitwidth {bitwidth}")
circ = RGQFTMultiplier(num_state_qubits=bitwidth)
return circ
Nota
Se si seleziona un kernel Python e il modulo qiskit non viene riconosciuto, provare a selezionare un ambiente Python diverso nel selettore di kernel.
Stimare l'algoritmo quantistico
Creare un'istanza dell'algoritmo usando la create_algorithm funzione . È possibile modificare le dimensioni del moltiplicatore modificando la bitwidth variabile.
bitwidth = 4
circ = create_algorithm(bitwidth)
Stimare le risorse fisiche per questa operazione usando i presupposti predefiniti. È possibile utilizzare la chiamata estimate, che è sovraccaricata per accettare un oggetto QuantumCircuit da Qiskit.
from qsharp.estimator import EstimatorParams
from qsharp.interop.qiskit import estimate
params = EstimatorParams()
result = estimate(circ, params)
In alternativa, è possibile usare il ResourceEstimatorBackend per eseguire la stima come fa il back-end esistente.
from qsharp.interop.qiskit import ResourceEstimatorBackend
from qsharp.estimator import EstimatorParams
params = EstimatorParams()
backend = ResourceEstimatorBackend()
job = backend.run(circ, params)
result = job.result()
L'oggetto result contiene l'output del processo di stima delle risorse. È possibile usare la funzione EstimateDetails per visualizzare i risultati in un formato più leggibile.
from qsharp_widgets import EstimateDetails
EstimateDetails(result)
La funzione EstimateDetails visualizza una tabella con i conteggi complessivi delle risorse fisiche. È possibile esaminare i dettagli dei costi espandendo i gruppi che contengono altre informazioni. Per altre informazioni, vedere i dati completi del report di Resource Estimator.
Ad esempio, se espandi il gruppo parametri qubit logici, è possibile vedere più facilmente che la distanza del codice di correzione degli errori è 15.
| Parametro qubit logico | Valore |
|---|---|
| Schema Correzione degli errori quantistici | surface_code |
| Distanza di codice | 15 |
| Qubit fisici | 450 |
| Tempo ciclo logico | 6us |
| Frequenza di errore del qubit logico | 3.00E-10 |
| Attraversamento del prefactoring | 0.03 |
| Soglia di correzione degli errori | 0,01 |
| Formula tempo del ciclo logico | (4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance |
| Formula qubit fisici | 2 * codeDistance * codeDistance |
Nel gruppo Parametri qubit fisici è possibile visualizzare le proprietà qubit fisiche che sono state considerate per questa stima. Ad esempio, il tempo per eseguire una misurazione a qubit singolo e un controllo a qubit singolo vengono considerati rispettivamente 100 ns e 50 ns.
Suggerimento
È anche possibile accedere all'output di Resource Estimator come dizionario Python usando il metodo result.data(). Ad esempio, per accedere ai conteggi fisici result.data()["physicalCounts"].
Diagrammi spazi
La distribuzione dei qubit fisici usati per l'algoritmo e le factory T è un fattore che può influire sulla progettazione dell'algoritmo. È possibile visualizzare questa distribuzione per comprendere meglio i requisiti di spazio stimati per l'algoritmo.
from qsharp_widgets import SpaceChart
SpaceChart(result)
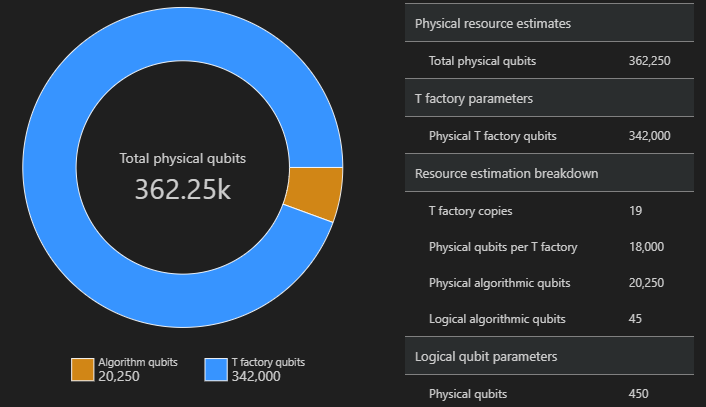
Il diagramma spaziale mostra la proporzione di qubit di algoritmo e qubit di T factory. Si noti che il numero di copie di fabbriche T, 19, contribuisce al numero di qubit fisici per le fabbriche T secondo l'equazione: $\text{fabbriche T} \cdot \text{qubit fisici per fabbrica T}= 19 \cdot 18.000 = 342.000$.
Per altre informazioni, vedere Stima fisica della factory T.
Modificare i valori predefiniti e stimare l'algoritmo
Quando si invia una richiesta di stima delle risorse per il programma, è possibile specificare alcuni parametri facoltativi. Usare il jobParams campo per accedere a tutti i valori che possono essere passati all'esecuzione del processo e verificare quali valori predefiniti sono stati considerati:
result.data()["jobParams"]
{'errorBudget': 0.001,
'qecScheme': {'crossingPrefactor': 0.03,
'errorCorrectionThreshold': 0.01,
'logicalCycleTime': '(4 * twoQubitGateTime + 2 * oneQubitMeasurementTime) * codeDistance',
'name': 'surface_code',
'physicalQubitsPerLogicalQubit': '2 * codeDistance * codeDistance'},
'qubitParams': {'instructionSet': 'GateBased',
'name': 'qubit_gate_ns_e3',
'oneQubitGateErrorRate': 0.001,
'oneQubitGateTime': '50 ns',
'oneQubitMeasurementErrorRate': 0.001,
'oneQubitMeasurementTime': '100 ns',
'tGateErrorRate': 0.001,
'tGateTime': '50 ns',
'twoQubitGateErrorRate': 0.001,
'twoQubitGateTime': '50 ns'}}
Questi sono i target parametri che è possibile personalizzare:
-
errorBudget- il budget complessivo degli errori consentiti -
qecScheme: schema di correzione degli errori quantistici (QEC) -
qubitParams: parametri qubit fisici -
constraints: i vincoli a livello di componente -
distillationUnitSpecifications: le specifiche per gli algoritmi di crittografia delle factory T
Per altre informazioni, vedere Target parametri per Lo strumento di stima delle risorse.
Modificare il modello qubit
Successivamente, stimare il costo per lo stesso algoritmo usando il parametro qubit basato su Majorana qubit_maj_ns_e6
qubitParams = {
"name": "qubit_maj_ns_e6"
}
result = backend.run(circ, qubitParams).result()
È possibile esaminare i conteggi fisici a livello di codice. Ad esempio, è possibile esplorare i dettagli sulla factory T creata per eseguire l'algoritmo.
result.data()["tfactory"]
{'eccDistancePerRound': [1, 1, 5],
'logicalErrorRate': 1.6833177305222897e-10,
'moduleNamePerRound': ['15-to-1 space efficient physical',
'15-to-1 RM prep physical',
'15-to-1 RM prep logical'],
'numInputTstates': 20520,
'numModulesPerRound': [1368, 20, 1],
'numRounds': 3,
'numTstates': 1,
'physicalQubits': 16416,
'physicalQubitsPerRound': [12, 31, 1550],
'runtime': 116900.0,
'runtimePerRound': [4500.0, 2400.0, 110000.0]}
Nota
Per impostazione predefinita, il runtime viene visualizzato in nanosecondi.
È possibile usare questi dati per produrre alcune spiegazioni del modo in cui le factory T producono gli stati T necessari.
data = result.data()
tfactory = data["tfactory"]
breakdown = data["physicalCounts"]["breakdown"]
producedTstates = breakdown["numTfactories"] * breakdown["numTfactoryRuns"] * tfactory["numTstates"]
print(f"""A single T factory produces {tfactory["logicalErrorRate"]:.2e} T states with an error rate of (required T state error rate is {breakdown["requiredLogicalTstateErrorRate"]:.2e}).""")
print(f"""{breakdown["numTfactories"]} copie(s) of a T factory are executed {breakdown["numTfactoryRuns"]} time(s) to produce {producedTstates} T states ({breakdown["numTstates"]} are required by the algorithm).""")
print(f"""A single T factory is composed of {tfactory["numRounds"]} rounds of distillation:""")
for round in range(tfactory["numRounds"]):
print(f"""- {tfactory["numUnitsPerRound"][round]} {tfactory["unitNamePerRound"][round]} unit(s)""")
A single T factory produces 1.68e-10 T states with an error rate of (required T state error rate is 2.77e-08).
23 copies of a T factory are executed 523 time(s) to produce 12029 T states (12017 are required by the algorithm).
A single T factory is composed of 3 rounds of distillation:
- 1368 15-to-1 space efficient physical unit(s)
- 20 15-to-1 RM prep physical unit(s)
- 1 15-to-1 RM prep logical unit(s)
Modificare lo schema di correzione degli errori quantistici
Eseguire di nuovo il processo di stima delle risorse per lo stesso esempio sui parametri qubit basati su Majorana con uno schema QEC floqued, qecScheme.
params = {
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"}
}
result_maj_floquet = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet)
Modificare il budget degli errori
Eseguire di nuovo lo stesso circuito quantistico con un valore errorBudget pari al 10%.
params = {
"errorBudget": 0.01,
"qubitParams": {"name": "qubit_maj_ns_e6"},
"qecScheme": {"name": "floquet_code"},
}
result_maj_floquet_e1 = backend.run(circ, params).result()
EstimateDetails(result_maj_floquet_e1)
Nota
Se si verifica un problema durante l'uso dello strumento di stima delle risorse, consultare la pagina Risoluzione dei problemi o contattare AzureQuantumInfo@microsoft.com.