VB.NET: Algoritmi genetici nella risoluzione di labirinti bidimensionali (it-IT)
Finalità
In questo articolo, da considerarsi come il seguito di «Algoritmo genetico per la generazione di icone in Visual Basic (it-IT)», vedremo come applicare gli algoritmi genetici per la risoluzione di problematiche delle quali non conosciamo a priori il modello finale, pur conoscendo quelli che sono i parametri ottimali da applicare. In altre parole, discuteremo gli algoritmi genetici nel contesto dell'ottimizzazione di soluzioni. Il linguaggio in cui svilupperemo l'applicazione di esempio sarà nuovamente Visual Basic .NET.
Introduzione
Nello scorso articolo abbiamo considerato come, a partire da un dato modello grafico, sia possibile generare un set di soluzioni caotiche/causali che evolvano verso l'obiettivo prefissato attraverso la costante selezione degli elementi migliori di ogni set, incrociandone le informazioni rappresentative per generare nuovi campioni probabilmente migliorativi. Nonostante si tratti di esempi interessanti, gli algoritmi genetici applicati al tendere verso un modello hanno l'ovvia particolarità di necessitare di una soluzione ideale di partenza/arrivo. Questo significa che se non disponiamo di un risultato finale cui proiettare/confrontare le soluzioni che vengono man mano generate, non vi sarà modo di evolvere oltre la dimensione del caos, chiudendo l'algoritmo in un ciclo infinito di esempi casuali, perché non orientati ad una qualsivoglia specificità.
Ovviamente, un algoritmo genetico deve sempre disporre - in qualche misura - di un obiettivo. Tuttavia, non è necessario fornire un modello monolitico cui tendere bensì, definite le condizioni ottimali che ci aspetteremmo, lasciare che l'algoritmo stesso trovi la soluzione che soddisfa tali requisiti, ovvero la soluzione ottimizzata ad un dato problema. Le applicazioni pratiche possibili sono tra le più svariate, e riguardano molti campi dello scibile umano. Dal momento però che uno dei campi che permette una migliore acquisizione di un concetto è il gioco, vedremo qui un esempio di implementazione in Visual Basic di un algoritmo genetico volto alla risoluzione di un labirinto 2D, cercando - tramite le funzionalità viste nel precedente articolo - non soltanto di unire due punti, ma di arrivare a farlo nel modo ottimale, ovvero cercando il percorso più breve.
Un breve riepilogo
Vediamo qui alcuni concetti già sottolineati in precedenza, ma utili da avere sottomano. Un algoritmo genetico è così chiamato perché cerca di mimare i processi biologici alla base dell'evoluzione delle specie. Si tratta cioè di creare un modello informatico capace di auto-adattarsi ad un dato contesto, generando individui (soluzioni ad un dato problema) che saranno impiegati per valutare il raggiungimento di un dato obiettivo. Il problema da risolvere è l'equivalente digitale del contesto biologico in cui gli individui si muovono, obbedendo al principio della sopravvivenza del più adatto. Nell'articolo precedente facevo l'esempio di un mondo popolato di predatori, in cui gli esseri più veloci (più predisposti alla fuga efficace) o più forti (più adatti alla resistenza attiva) rappresentavano candidati migliori per la sopravvivenza rispetto a esemplari più lenti o meno pugnaci. Allo stesso modo, se informaticamente disponiamo di un obiettivo (l'equivalente del parametro base della sopravvivenza biologica), potremo parlare di "invidui adatti" nella misura in cui potenziali soluzioni si avvicinano all'obiettivo prefisso. Tra queste, allo stesso modo di quanto accade in natura, cercheremo - individuate le migliori - di generare soluzioni figlie, che condividano i caratteri dei genitori. Un esempio lampante di ciò è quanto è stato mostrato nel primo articolo: data un'icona grafica (un insieme di byte che produce una data immagine), e partendo da un certo numero di soluzioni caotiche, ad ogni generazione le soluzioni migliori sono quelle che più si avvicinano alla forma del modello cui si ispirano.
L'ispirazione alla biologia da parte degli algoritmi genetici passa altresì per la sua terminologia. In essa, distinguiamo:
- Il concetto di cromosoma/individuo, ovvero la singola soluzione ad un dato problema;
- La popolazione, ovvero l'insieme delle possibili soluzioni;
- Il gene, o la parte (byte) di un individuo;
- L'adeguatezza, intesa come la percentuale di validità di una soluzione/individuo;
- Il crossing-over, ovvero la ricombinazione delle soluzioni in nuovi modelli (nuovi cromosomi/individui);
- La mutazione, intesa come i cambiamenti casuali (o pseudo tali) che possono prodursi all'interno di una soluzione qualsiasi.
Tutti questi concetti sono validi in campo informatico, e necessitano di essere in qualche modo implementati per poter parlare di una vera soluzione basata sugli algoritmi genetici, ossia capace di autoevolvere. Sta allo sviluppatore definire ciascuno di essi, sia in termini teorici che in quelli più pratici dello svolgimento di ciascuna fase.
Ottimizzare una soluzione
In linea di massima, anche citando il caso della replica speculare di un'immagine, parlando di un algoritmo genetico (AG) si può sempre parlare di ottimizzazione. In effetti, qualsiasi caso ad esso applicato è, in ultima analisi, la ricerca della migliore soluzione, sia che questo contempli il suo raggiungimento ideale o che ricada in un ottimo locale considerato soddisfacente. Con il termine "ottimo locale" indichiamo l'incapacità di progredire oltre un certo livello di precisione a causa di caratteristiche interne alla popolazione che, ricombinandosi, non generino migliorie. Una prevenzione a questo fattore viene applicato attraverso la mutazione, con la quale introduciamo, su base casuale, delle modifiche ulteriori alla replica genetica delle due soluzioni, in modo da avere sempre un minimo di caos nella trasmissione delle informazioni da una generazione alla successiva.
Nonostante sia sempre possibile riferirsi al concetto di ottimizzazione, esso diventa più evidente se lo applichiamo alla soluzione di un problema logistico. Supponiamo di trovarci all'interno di un labirinto, che fornisca più possibilità per arrivare a destinazione. In esso, potremo muoverci come la topografia del labirinto stesso ci consente, e non è da escludersi che potremmo anche tornare sui nostri passi, magari non arrivando mai a destinazione. In sostanza, in un simile labirinto ci sono molti modi per giungere ad una soluzione...ma sicuramente ne esiste almeno una che è migliore di altre. In un luogo del genere, la strada migliore è quella che ci conduce dal punto di partenza a quello di destinazione in modo diretto, nel minor numero di mosse/passi possibile (soluzione ottima/ottimizzata). Ed un algoritmo genetico può aiutarci ad individuare quel percorso, senza sapere a priori quali siano le possibilità. Vediamo quindi che non si tratta soltanto di trovare una soluzione, ma di saggiarne la bontà, in vista di ricercare quella migliore.
La struttura di base
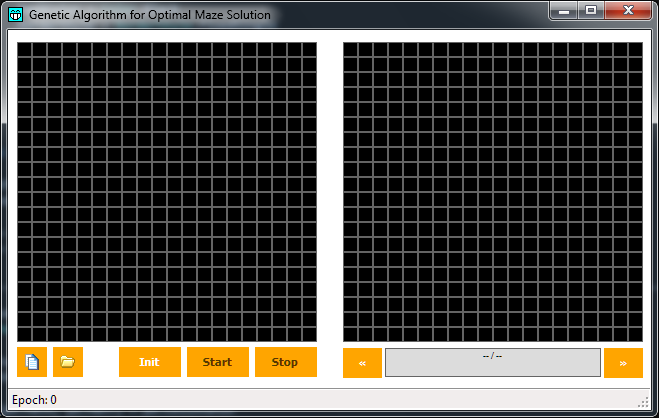
Per poter ragionare su un labirinto, dobbiamo anzitutto disporre di un labirinto. Qui a seguire evidenzio le basi che ho utilizzato nel mio esempio, in modo da far comprendere su quali basi ci troveremo ad operare. Come di consueto, alla fine di questo articolo è presente il link al quale scaricare il codice di esempio, che invito a consultare per i dettagli che in queste righe non vengono analizzati. Eseguendo il codice allegato, ci si troverà dinanzi ad una videata di questo tipo:
Si nota cioè che vengono create due finestre di lato 20 x 20 celle, le quali verranno impiegate come rappresentazione grafica degli elementi costituenti il labirinto definito dall'utente (sulla sinistra) e quello che mostrerà le varie soluzioni trovate dal programma (sulla destra). Nel riquadro di sinistra, è possibile cliccare ciascuna cella un certo numero di volte. Segue uno schema di corrispondenza tra il numero di clic eseguito ed il valore assunto dalla cella in questione:
1 Clic = Cella "Muro" (colore grigio, sarà considerata invalicabile)
2 Clic = Punto di partenza (colore verde, il punto di ingresso nel labirinto)
3 Clic = Punto di arrivo (colore rosso, il punto di uscita dal labirinto)
4 Clic = Cella considerata valida (non usata in questo contesto, sarà impiegata dall'algoritmo)
5 Clic = Cella "Libera" (colore nero, una cella considerata attraversabile)
Per rendere le cose un po' più rapide nel caso si desideri fare qualche test alternativo, ho implementato due tasti per effettuare il salvataggio e successivo caricamento di file di labirinto. Nel codice sorgente è fornito il file "test_maze.txt" per l'esempio qui in esame. Caricando tale file, si ottiene il labirinto che segue:
Si nota immediatamente che tra i due punti definiti come partenza ed arrivo esistono molteplici soluzioni possibili. Ma prima di indagare la parte legata all'algoritmo genetico, spendo qualche riga per illustrare come è stato creato il labirinto, e su quale logica operativa soggiace: sarà utile per capire meglio il funzionamento dell'algoritmo.
Implementazione labirinto in VB
Il nostro labirinto ha, come base fondante, un array a due dimensioni di Byte di nome sourceMaze(). Ad ogni cella del labirinto corrisponde cioè una posizione interna a tale array, nella forma (X, Y). Ciascuno di tali bytes è valorizzato in modo da rappresentare lo stato di quella particolare cella. Per comodità, tali stati sono riassunti in un'enumerazione, presente nel file Globals.vb:
Module Globals
Public Const MAZESIZE As Byte = 20
Public Const MAZESIDE As Byte = 15
Public Enum CELLSTATE
Free = 0
Wall = 1
Start = 2
Finish = 3
Valid = 4
FakeWall = 5
End Enum
End Module
Si noterà la presenza di un valore ulteriore rispetto a quelli citati sopra, ovvero FakeWall = 5. Ne parleremo tra poco, quando vedremo come vengano generate le soluzioni.
In ingresso al Form, viene chiamata una routine preposta alla generazione grafica dei labirinti. Ciò viene fatto mediante l'impiego di controlli MazeCell, estensione del PictureBox standard creata ad hoc per contenere i valori corrispondenti alla matrice dei dati.
Private Sub GenerateMaze(container As Panel)
Dim _TOP As Integer = 0
Dim _LEFT As Integer = 0
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
Dim pb As New MazeCell
With pb
.Name = container.Name & _Y.ToString("00") & _X.ToString("00")
.Top = _TOP
.Left = _LEFT
.Width = MAZESIDE
.Height = MAZESIDE
.BackColor = Color.Black
.BorderStyle = BorderStyle.FixedSingle
.Cursor = Cursors.Hand
.MatX = _X
.MatY = _Y
AddHandler pb.Click, AddressOf MazeClickCell
End With
_LEFT += MAZESIDE
container.Controls.Add(pb)
Next
_LEFT = 0
_TOP += MAZESIDE
Next
End Sub
GenerateMaze() necessita di un parametro Panel, che rappresenta il controllo padre all'interno del quale generare la struttura. Successivamente, attraverso due loop annidati, si creano le celle che saranno legate all'array sourceMaze durante l'evento MazeClickCell, definito come segue:
Private Sub MazeClickCell(sender As Object, e As EventArgs)
Dim pb As MazeCell = CType(sender, MazeCell)
pb.CellStatus += 1
If pb.CellStatus > CELLSTATE.Valid Then pb.CellStatus = CELLSTATE.Free
sourceMaze(pb.MatX, pb.MatY) = pb.CellStatus
pb.BackColor = pb.CellBrush
End Sub
Si nota quindi che i controlli di tipo MazeCell, rispetto ad un PictureBox tradizionale, dispongono delle proprietà MatX, che identifica l'ascissa della cella nella matrice, MatY, che rappresenta l'ordinata, CellStatus, che espone il contenuto della cella, e CellBrush, che relativamente allo stato della cella la rappresenti mediante un colore. Il codice che realizza l'estensione MazeCell è il seguente:
Public Class MazeCell
Inherits PictureBox
Dim _STATUS As Byte = 0
Dim _MATX As Byte = 0
Dim _MATY As Byte = 0
Public Property CellStatus As Byte
Get
Return _STATUS
End Get
Set(value As Byte)
_STATUS = value
End Set
End Property
Public ReadOnly Property CellBrush As Color
Get
Select Case CellStatus
Case CELLSTATE.Free
Return Color.Black
Case CELLSTATE.Valid
Return Color.Violet
Case CELLSTATE.Start
Return Color.Green
Case CELLSTATE.Finish
Return Color.Red
Case CELLSTATE.Wall
Return Color.Gray
Case CELLSTATE.FakeWall
Return Color.Yellow
End Select
End Get
End Property
Public Property MatX As Byte
Get
Return _MATX
End Get
Set(value As Byte)
_MATX = value
End Set
End Property
Public Property MatY As Byte
Get
Return _MATY
End Get
Set(value As Byte)
_MATY = value
End Set
End Property
Public ReadOnly Property StringMatrix As String
Get
Return _MATX.ToString & ";" & _MATY.ToString
End Get
End Property
End Class
Questa struttura permette, lato utente, la definizione del labirinto di base, da fornire poi come base all'algoritmo genetico, o salvare per referenza futura (non mi dilungo qui sulle routine di salvataggio e caricamento, che sono rese funzionali ma non ottimizzate, dal momento che ho preferito concentrare l'attenzione sugli aspetti fondamentali dell'esempio).
Logica dell'algoritmo genetico
Terminata la definizione del contesto operativo, possiamo ragionare sulle possibilità esplorative di un automa. Più sopra abbiamo accennato alle regole da applicare per ciascuna tipologia di cella, e sappiamo quindi quali siano i requisiti di base che deve avere un algoritmo generico (attenzione: generico, non genetico) di esplorazione. Sappiamo che deve iniziare a muoversi a partire dalla cella verde, tentare di raggiungere quella rossa, e non può valicare le celle grigie. Tutte le celle nere/libere possono essere esplorate. Possiamo quindi pensare ad una routine che, dato un punto di partenza, valuti in base a quello stesso punto la condizione delle quattro celle adiacenti, e si sposti ricorsivamente su ciascuna di quelle considerate attraversabili.
Detto il altri termini, considerando l'array solverBytes() come la matrice contenente una determinata soluzione, una funzione di questo tipo:
Private Function Solve(_X As Integer, _Y As Integer) As Boolean
If solverBytes(_endPos(0), _endPos(1)) = CELLSTATE.Valid Then Return True
If solverBytes(_X + 1, _Y) = CELLSTATE.Free Or solverBytes(_X + 1, _Y) = CELLSTATE.Start Or solverBytes(_X + 1, _Y) = CELLSTATE.Finish Then
solverBytes(_X + 1, _Y) = CELLSTATE.Valid
If Solve(_X + 1, _Y) Then Return True
End If
If solverBytes(_X - 1, _Y) = CELLSTATE.Free Or solverBytes(_X - 1, _Y) = CELLSTATE.Start Or solverBytes(_X - 1, _Y) = CELLSTATE.Finish Then
solverBytes(_X - 1, _Y) = CELLSTATE.Valid
If Solve(_X - 1, _Y) Then Return True
End If
If solverBytes(_X, _Y + 1) = CELLSTATE.Free Or solverBytes(_X, _Y + 1) = CELLSTATE.Start Or solverBytes(_X, _Y + 1) = CELLSTATE.Finish Then
solverBytes(_X, _Y + 1) = CELLSTATE.Valid
If Solve(_X, _Y + 1) Then Return True
End If
If solverBytes(_X, _Y - 1) = CELLSTATE.Free Or solverBytes(_X, _Y + 1) = CELLSTATE.Start Or solverBytes(_X, _Y + 1) = CELLSTATE.Finish Then
solverBytes(_X, _Y - 1) = CELLSTATE.Valid
If Solve(_X, _Y - 1) Then Return True
End If
Return False
End Function
Come è possibile notare, dato un punto di partenza individuabile alle coordinate [_X,_Y], la funzione cicla finchè non individua tutte le celle libere che conducono alla soluzione, ovvero ad avere la cella finale come valida. Detto in altri termini, tale algoritmo esplora l'intero dominio delle soluzioni. Applicando tale funzione al labirinto di cui sopra, otterremmo cioé una soluzione di questo tipo:
Ovviamente si tratta di una soluzione onnicomprensiva, che ha il solo fine di tracciare tutte le possibilità. Si tratta cioè della soluzione valida più dispersiva in assoluto. Ha il suo utilizzo in contesti particolari (si noti che, a livello di concetto, si tratta banalmente di un floodfill grafico internamente a margini definiti), ma non è ciò che desideriamo ottenere in questa sede. Qui stiamo entrando in contatto con quelle che sono le particolarità di un AG: cosa deve essere in grado di fare? Nel nostro caso, deve cercare di risolvere un labirinto, ma senza accanirsi nell'occupazione massiva dello spazio di movimento. Così, nel generare più individui dotati della capacità di risolvere il problema, potremmo introdurre una sorta di limitatore.
L'abbiamo intravisto sopra, nell'enumerazione CELLSTATE, con il valore di FakeWall = 5. Mentre generiamo un individuo, andiamo cioè a "sporcare" la soluzione della funzione Solve() con dei "muri virtuali", ovvero non presenti nella struttura base del labirinto, ma che hanno l'effetto di alterare le possibilità risolutive dell'algoritmo stesso.
Per semplicità di rappresentazione, renderizzeremo tali blocchi con il colore giallo. Come detto, si tratta di limiti arbitrari, che rispondono alle stesse leggi di invalicabilità dei muri tradizionali, e che vanno a limitare, per ciascun individuo creato, il dominio delle soluzioni. Si noti infatti che, laddove è presente un blocco giallo, non viene proseguita l'esplorazione a partire da quella cella specifica. Tale casualità ci permette di generare una popolazione di individui varia: conterrà elementi che risolveranno il labirinto, e altri che non riusciranno (pensiamo ad un blocco giallo subito davanti alla cella finale). Ciascuna soluzione, poi, completerà il suo ciclo in un certo numero di passi. Ci saranno elementi che arriveranno a destinazione in modo più diretto rispetto ad altre più arzigogolate, e quindi dispersive.
Implementazione soluzione potenziale in VB
Qui a seguire, riporto il listato della classe GASolver, che rappresenta il singolo individuo/soluzione. Si noti che essa è dotata di un costruttore generico, che accetta in ingresso l'array del labirinto creato dall'utente, per replicare in ciascuna soluzione i bytes relativi ai muri fisici, ed ai punti di partenza e arrivo, che sono requisiti imprescindibili nella risoluzione del labirinto. Con una certa probabilità, vengono valorizzate una o più celle mediante il valore FakeWall, per apporre dei limiti ulteriori laddove l'utente, nella creazione del labirinto, ha lasciato degli spazi percorribili.
Public Class GASolver
Dim _startpos(1) As Byte
Dim _endPos(1) As Byte
Dim _isSolved As Boolean
Dim solverBytes(MAZESIZE, MAZESIZE) As Byte
Public ReadOnly Property StartPos As Byte()
Get
Return _startpos
End Get
End Property
Public ReadOnly Property EndPos As Byte()
Get
Return _endPos
End Get
End Property
Public ReadOnly Property GetBytes As Byte(,)
Get
Return solverBytes
End Get
End Property
Public ReadOnly Property Steps As Integer
Get
Dim _steps As Integer = 0
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If solverBytes(_X, _Y) = CELLSTATE.Valid Then _steps += 1
Next
Next
Return _steps
End Get
End Property
Public ReadOnly Property isSolved As Boolean
Get
Return Solve(_startpos(0), _startpos(1))
End Get
End Property
Private Function Solve(_X As Integer, _Y As Integer) As Boolean
If solverBytes(_endPos(0), _endPos(1)) = CELLSTATE.Valid Then Return True
If solverBytes(_X + 1, _Y) = CELLSTATE.Free Or solverBytes(_X + 1, _Y) = CELLSTATE.Start Or solverBytes(_X + 1, _Y) = CELLSTATE.Finish Then
solverBytes(_X + 1, _Y) = CELLSTATE.Valid
If Solve(_X + 1, _Y) Then Return True
End If
If solverBytes(_X - 1, _Y) = CELLSTATE.Free Or solverBytes(_X - 1, _Y) = CELLSTATE.Start Or solverBytes(_X - 1, _Y) = CELLSTATE.Finish Then
solverBytes(_X - 1, _Y) = CELLSTATE.Valid
If Solve(_X - 1, _Y) Then Return True
End If
If solverBytes(_X, _Y + 1) = CELLSTATE.Free Or solverBytes(_X, _Y + 1) = CELLSTATE.Start Or solverBytes(_X, _Y + 1) = CELLSTATE.Finish Then
solverBytes(_X, _Y + 1) = CELLSTATE.Valid
If Solve(_X, _Y + 1) Then Return True
End If
If solverBytes(_X, _Y - 1) = CELLSTATE.Free Or solverBytes(_X, _Y + 1) = CELLSTATE.Start Or solverBytes(_X, _Y + 1) = CELLSTATE.Finish Then
solverBytes(_X, _Y - 1) = CELLSTATE.Valid
If Solve(_X, _Y - 1) Then Return True
End If
Return False
End Function
Public Sub New(bytes01(,) As Byte, bytes02(,) As Byte, startPos As Byte(), endPos As Byte())
_startpos = startPos
_endPos = endPos
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If bytes01(_X, _Y) = CELLSTATE.Wall Then solverBytes(_X, _Y) = bytes01(_X, _Y)
If bytes01(_X, _Y) = CELLSTATE.FakeWall Then solverBytes(_X, _Y) = bytes01(_X, _Y)
Next
Next
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If bytes02(_X, _Y) = CELLSTATE.Wall Then solverBytes(_X, _Y) = bytes02(_X, _Y)
If bytes02(_X, _Y) = CELLSTATE.FakeWall Then solverBytes(_X, _Y) = bytes02(_X, _Y)
Next
Next
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If solverBytes(_X, _Y) <> CELLSTATE.Wall Then
Randomize()
If Int(Rnd() * 100) Mod 99 = 0 Then
If Int(Rnd() * 100) Mod 99 = 0 Then
solverBytes(_X, _Y) = CELLSTATE.FakeWall
Else
solverBytes(_X, _Y) = CELLSTATE.Free
End If
End If
End If
Next
Next
solverBytes(startPos(0), startPos(1)) = CELLSTATE.Start
solverBytes(endPos(0), endPos(1)) = CELLSTATE.Finish
End Sub
Public Sub New(sourceBytes(,) As Byte)
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If sourceBytes(_X, _Y) = CELLSTATE.Start Then _startpos(0) = _X : _startpos(1) = _Y
If sourceBytes(_X, _Y) = CELLSTATE.Finish Then _endPos(0) = _X : _endPos(1) = _Y
If sourceBytes(_X, _Y) = CELLSTATE.Free Then
Randomize()
If Int(Rnd() * 100) Mod 50 = 0 Then
solverBytes(_X, _Y) = CELLSTATE.FakeWall
Else
solverBytes(_X, _Y) = CELLSTATE.Free
End If
Else
solverBytes(_X, _Y) = sourceBytes(_X, _Y)
End If
Next
Next
End Sub
End Class
È inoltre presente la funzione Solve() vista sopra, che permetterà di capire se una data soluzione arriva al punto di destinazione, o se fallisce in un altro punto. Vi sono poi altre proprietà e funzioni che analizzeremo tra breve.
Fitness di una soluzione
Come già descritto nel precedente articolo, particolarità irrinunciabile di un algoritmo genetico è quella di poter calcolare un punteggio di adattabilità rispetto ad un problema qualunque. Va da sé che il modo in cui detto punteggio verrà calcolato dipende dalla tipologia del problema. Il fitness è fondamentale perchè, data una popolazione costituita da elementi più o meno vicini a ciò che ci prefissiamo, permette di estrarre quei campioni dalle cui caratteristiche vorremmo poter creare nuovi esemplari migliorativi. È pertanto evidente come l'errata progettazione della funzione del calcolo del fitness sia il fondamento di un eventuale fallimento nella realizzazione di un AG.
Per cercare di limitare problematiche relative all'errata attribuzione del fitness ad una o più soluzioni, è fondamentale analizzare a fondo la problematica. È più semplice se ci interessa, come nel primo articolo, replicare un'immagine: sappiamo che essa è - in fondo - un insieme di bytes ordinati in un dato modo, quindi il fitness di una soluzione passa per la verifica di quanti bytes siano uguali all'obiettivo in ciascun individuo della popolazione. In caso di problemi "aperti", come il presente, è necessario un passo in più. Qui infatti non ci interessa l'affinità ad un modello predefinito, bensì l'efficacia potenziale di una soluzione.
Semplificando, nel caso di un labirinto ci interessano fondamentalmente due aspetti, già accennati sopra:
- Che sia una soluzione valida, ovvero che arrivi a destinazione
- Che sia una soluzione rapida, ovvero che, dato per requisito fondamentale il punto 1), riesca ad ottenerlo il più concisamente possibile
Possiamo quindi dire che, nel nostro caso, la determinazione del nostro fitness passa per due proprietà: la prima è la solvibilità, mentre la seconda è il numero di passi validi effettuati, dove minore è il valore, maggiore è la qualità della soluzione. A questo fine, la classe GASolver implementa le due rispettive proprietà: isSolved, che restituisce un booleano utile a comprendere se l'individuo raggiunge il punto di destinazione, e Steps, che conta il numero di celle valide presenti nella soluzione stessa.
Inizializzazione e cross-over
Il concetto di inizializzazione segue regole semplici: si tratta di creare una prima generazione di soluzioni, usando i normali costruttori. Nel codice allegato, ciò viene compiuto alla pressione del tasto btnInit:
Private Sub btnInit_Click(sender As Object, e As EventArgs) Handles btnInit.Click
epochs = 0
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If sourceMaze(_X, _Y) = CELLSTATE.Start Then _startPos(0) = _X : _startPos(1) = _Y
If sourceMaze(_X, _Y) = CELLSTATE.Finish Then _endPos(0) = _X : _endPos(1) = _Y
Next
Next
gaList = New List(Of GASolver)
For ii As Integer = 0 To 999
gaList.Add(New GASolver(sourceMaze))
Next
gaCursor = 0
MazePaintItem(mazeDest)
btnStart.Enabled = True
btnStop.Enabled = False
End Sub
Viene portato a zero un contatore che servirà per il conteggio delle generazioni, dopodichè si determinano le caselle che l'utente ha definito essere i punti di partenza e arrivo. In una comoda struttura di tipo List(Of GASolver), che interrogheremo via LINQ, aggiungiamo un numero arbitrario di nuovi elementi GASolver (nel caso in esame, 1000 unità), per poi procedere alla loro rappresentazione grafica. Ciascuna soluzione iniziale, come abbiamo visto, sarà inizializzata aggiungendo limiti fittizi in alcuni spazi lasciati vuoti dall'utente, in modo da creare varietà nella popolazione.
Alla pressione del tasto btnStart, viene lanciata la ricerca di soluzioni. Si noti come nel loop vengano estratti dalla lista gaList gli elementi che risolvono il labirinto (ga.isSolved = True), ordinati per il numero di passi necessari a completare la procedura, ordinati in modo ascendente (Order By ga.Steps Ascending). In questo modo, saremo certi di estrarre le due soluzioni migliori. Tali elementi verranno ricombinati tra di loro, producendo due nuovi elementi, secondo le regole che vedremo tra un attimo. Infine, ordinando la lista per il numero discendente di passi, scartiamo due elementi tra quelli vecchi. Si noti che non applichiamo qui discriminanti sulla validità della soluzione, ed è possibile quindi che vengano eliminati elementi risolutivi, aventi però la pecca di essere - tra tutte le soluzioni, valide e non - quelle più dispendiose.
Il cross-over che genera i due nuovi elementi è esemplificato nella funzione New() a quattro argomenti della classe GASolver.
Essa è come segue:
Public Sub New(bytes01(,) As Byte, bytes02(,) As Byte, startPos As Byte(), endPos As Byte())
_startpos = startPos
_endPos = endPos
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If bytes01(_X, _Y) = CELLSTATE.Wall Then solverBytes(_X, _Y) = bytes01(_X, _Y)
If bytes01(_X, _Y) = CELLSTATE.FakeWall Then solverBytes(_X, _Y) = bytes01(_X, _Y)
Next
Next
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If bytes02(_X, _Y) = CELLSTATE.Wall Then solverBytes(_X, _Y) = bytes02(_X, _Y)
If bytes02(_X, _Y) = CELLSTATE.FakeWall Then solverBytes(_X, _Y) = bytes02(_X, _Y)
Next
Next
For _Y As Integer = 0 To MAZESIZE - 1
For _X As Integer = 0 To MAZESIZE - 1
If solverBytes(_X, _Y) <> CELLSTATE.Wall Then
Randomize()
If Int(Rnd() * 100) Mod 99 = 0 Then
If Int(Rnd() * 100) Mod 99 = 0 Then
solverBytes(_X, _Y) = CELLSTATE.FakeWall
Else
solverBytes(_X, _Y) = CELLSTATE.Free
End If
End If
End If
Next
Next
solverBytes(startPos(0), startPos(1)) = CELLSTATE.Start
solverBytes(endPos(0), endPos(1)) = CELLSTATE.Finish
End Sub
In sostanza, necessita in ingresso delle matrici riferite ai due elementi da combinare, più le coordinate dei punti di inizio e fine del labirinto.
Ciclando all'interno delle due matrici, assegna ad una matrice risultante la combinazione dei tipi cella Wall e FakeWall. Al di là del fatto che i tipi Wall sono coincidenti per entrambe le matrici, i FakeWall verosimilmente non lo saranno. Se però entrambe le soluzioni risolvono l'algoritmo, significa che i FakeWall di entrambe le matrici in ingresso possono essere applicate senza inficiare la soluzione, ma - anzi - migliorandola, eliminando potenziali spazi liberi che vengano considerati come step validi. Terminato questo procedimento, un ulteriore loop di mutazione calcola l'eventuale trasformazione di celle non-muro in celle Wall o FakeWall. La soluzione appena prodotta avrà quindi gli stessi muri e punti di inizio/arrivo dei genitori, ma i muri virtuali di entrambi, con le mutazioni (se avverranno) del caso.
La logica è semplice: ciò che determina una soluzione più economica rispetto ad una più dispersiva, è la libertà di movimento. Tante più sono le celle libere, tanto maggiore sarà il dominio delle soluzioni e, di conseguenza, i passi che verranno compiuti verso l'uscita. Nel modo sopra descritto, si applica una limitazione progressiva verso un cammino essenziale, costituito dalla sommatoria dei limiti che, nelle generazioni precedenti, hanno rappresentato un aiuto verso tale fine.
Lasciando che l'algoritmo avvicendi le generazioni, entro poche centinaia di epoche avremo la soluzione ottimale, ovvero quella che conduce dalla partenza all'arrivo senza scarti di sorta. Al tempo stesso, l'eliminazione progressiva delle soluzioni scadenti in favore di quelle più performanti condurrà ad avere un'intera popolazione di soluzioni accettabili.
Nell'esempio qui sopra, è possibile notare come dopo circa 14000 generazioni di soluzioni, il risultato sia vicino a quello ottimale: c'è ancora spazio per migliorie, che proseguendo nell'elaborazione potranno essere raggiunte, seppur con la lentezza dovuta dalla ricombinazione di soluzioni molto vicine all'ideale (che possono cioè quasi esclusivamente contare sulla mutazione, per migliorare ancora). Si consideri inoltre che - date più soluzioni - la direzione intrapresa dall'algoritmo si modifica a seconda delle elaborazioni: se in una mutazione viene inibito un certo passaggio, allora l'algoritmo si concentrerà sulle soluzioni restanti. Non verrà quindi determinata la migliore nel senso assoluto del termine, bensì la migliore secondo il contesto corrente e gli agenti a disposizione, mimando a livello concettuale ciò che accade anche nella biologia.
Codice sorgente di esempio
Video dimostrativo
- È possibile visionare una sessione di esempio del programma qui trattato, a questo indirizzo: http://youtu.be/4cqsjThCrRA
Bibliografia
- http://en.wikipedia.org/wiki/DNA
- http://en.wikipedia.org/wiki/Natural_selection
- http://en.wikipedia.org/wiki/Genetic_algorithm
- Algoritmo genetico per la generazione di icone in Visual Basic (it-IT)
Altre lingue
Questo articolo è disponibile anche in Inglese: