Algorithmes de création de transformation WCS

Création de transformations

 

Exécution séquentielle de transformation

 

Création de transformations optimisées

 

ICCProfileFromWCSProfile

 

Black Preservation et Black Generation

 

Vérifier la gamme

Création de transformations

Pour expliquer correctement le fonctionnement des transformations de couleur, il est utile d’expliquer le chemin de traitement complet à la fois par ICM 2.0 et les éléments internes de l’objet CTE. La fonction CreateColorTransformW ICM 2.0 crée une transformation de couleur que les applications peuvent utiliser pour effectuer la gestion des couleurs. Cette fonction crée un contexte de couleur à partir des entrées LOGCOLORSPACE et intention. Les intentions sont mappées à des corrélations d’algorithme de mappage de gamut ICC de base. La fonction appelle ensuite la fonction ICM 2.0 CreateMultiProfileTransform pour un traitement cohérent des couleurs. La fonction CreateColorTransform copie généralement les données dans la structure de transformation optimisée interne.

La fonction CreateMultiProfileTransform ICM 2.0 accepte un tableau de profils et un tableau d’intentions ou un profil de liaison d’appareil unique, et crée une transformation de couleur que les applications peuvent utiliser pour effectuer un mappage de couleurs. Il traite ces profils et intentions d’entrée pour créer des modèles d’appareil, des modèles d’apparence de couleur, des descriptions de limites de gamut et des modèles de mappage de gamut. Voici comment procéder :

• Les modèles d’appareil sont initialisés directement à partir des profils DM. Un modèle d’appareil est créé pour chaque profil dans l’appel à CreateMultiProfileTransform.
• Les modèles d’apparence de couleur sont initialisés directement à partir des profils CAM. Il existe un profil CAM pour chaque profil dans l’appel à CreateMultiProfileTransform. Toutefois, le même profil CAM peut être spécifié pour plusieurs profils.
• Les descriptions des limites de gamut sont initialisées à partir d’un objet de modèle d’appareil et d’un objet CAM. Il existe une description de limite de gamut pour chaque profil dans l’appel à CreateMultiProfileTransform.
• Les modèles de mappage de gamut sont initialisés à partir de deux limites de gamut et d’une intention. Vous devez créer un modèle de mappage de gamut entre chaque paire de modèles d’appareil créée à partir de l’appel à CreateMultiProfileTransform. Notez que cela signifie que vous utilisez un modèle de carte de gamut de moins que le modèle d’appareil. Étant donné que le nombre d’intentions correspond au nombre de modèles d’appareil, il y a également une intention de plus que nécessaire. La première intention de la liste est ignorée. Vous parcourez la liste des modèles d’appareils et des intentions, en créant des modèles de mappage de gamut. Récupérez les premier et deuxième modèles d’appareil et la deuxième intention, puis initialisez le premier modèle de mappage de gamut. Récupérez les deuxième et troisième modèles d’appareil et la troisième intention, puis initialisez le deuxième modèle de mappage de gamut. Continuez de cette manière jusqu’à ce que vous ayez créé tous les modèles de mappage de gamut.

Lorsque les profils ont été correctement traités et que tous les objets intermédiaires ont été créés et initialisés, vous pouvez créer la transformation CITE avec l’appel suivant. Les valeurs pDestCAM et pDestDM sont celles associées au dernier profil dans l’appel à CreateMultiProfileTransform.

HRESULT CreateCITEColorTransform(
 __inout     IDeviceModel          *pSourceDM,
 __inout     IColorAppearanceModel *pSourceCAM,
 __in        GamutMapArray         *pGamutMapArray,
 __inout     IColorAppearanceModel *pDestCAM,
 __inout     IDeviceModel          *pDestDM,
             EColorTransformMode    eTransformMode,
 __deref_out IColorTransform      **ppCTS
 );

Prise en charge des plug-ins

Un problème lié à la configuration de la liste de transformation consiste à vérifier si un plug-in requis est disponible. Le commutateur de modèle suivant fournit cette stratégie pour contrôler ce comportement. La gestion de cette liste de transformations est une méthode dans la structure de transformation optimisée interne, mais chaque méthode de modèle fournit le pointeur vers elle-même et son propre ensemble de valeurs de paramètres.

Le mode doit être l’un des suivants.

• TfmRobust : si un profil de mesure spécifie un plug-in préféré et que le plug-in n’est pas disponible, le nouveau système DTE utilise le plug-in de base. Si aucun plug-in n’est disponible, la transformation signale une erreur.
• TfmStrict : si ColorContext spécifie un plug-in préféré, le plug-in doit être disponible. Si aucun plug-in préféré n’est trouvé, le plug-in de base est utilisé. Si aucun plug-in n’est disponible, la transformation signale une erreur.
• TfmBaseline : seuls les plug-ins de base peuvent être utilisés dans AddMeasurementStep. Si colorContext spécifie un plug-in préféré, le plug-in est ignoré. Si le plug-in de base n’est pas disponible, la transformation signale une erreur.

Exécution de la transformation

La fonction TranslateColors de l’API ICM 2.0 traduit un tableau de couleurs de l’espace de couleur source vers l’espace de couleur de destination tel que défini par une transformation de couleur. Cette fonction vérifie en interne un tableau de couleurs mises en cache pour permettre une correspondance immédiate des couleurs couramment transformées. Cette transformation prend en charge les tableaux d’octets 8 bits par canal et les tableaux float 32 bits par canal. Tous les autres formats seront convertis avant de passer à la nouvelle table DTE.

La fonction TranslateBitmapBitBitBits de l’API ICM 2.0 traduit les couleurs d’une bitmap ayant un format défini pour produire une autre bitmap dans un format demandé. Cette fonction vérifie en interne un tableau de couleurs mises en cache pour permettre une correspondance immédiate des couleurs couramment transformées. Pour éviter un trop grand nombre de chemins de code, la prise en charge et la complexité des tests, seuls un nombre limité de formats bitmap sont réellement pris en charge dans le moteur de transformation et d’interpolation. Cette fonction doit traduire les formats bitmap entrants et sortants non natifs en formats pris en charge en mode natif pour le traitement. Cette transformation prend uniquement en charge les bitmaps d’octets 8 bits par canal et les bitmaps flottantes 32 bits par canal. Tous les autres formats seront convertis avant de passer à la nouvelle table DTE.

 

Exécution séquentielle de transformation

Si le paramètre dwFlags a le SEQUENTIAL_TRANSFORM bit défini lorsque les fonctions ICM CreateColorTransformW ou CreateMultiProfileTransform sont appelées, les étapes de transformation sont exécutées séquentiellement. Cela signifie que le code parcoure séparément chaque modèle d’appareil, modèle d’apparence de couleur et modèle de mappage de gamut, comme spécifié par l’appel CreateColorTransform ou CreateMultiProfileTransform . Cela peut être utile pour le débogage des modules de plug-in, mais il est beaucoup plus lent que l’exécution via une transformation optimisée. L’exécution en mode séquentiel n’est donc pas recommandée pour les logiciels de production. En outre, il peut y avoir de légères différences dans les résultats obtenus en mode séquentiel et en mode optimisé. Cela est dû aux variations introduites lorsque les fonctions sont concaténées ensemble.

Création de transformations optimisées

Une transformation optimisée est une table de choix multidimensionnelle. La table peut être traitée par un moteur d’interpolation multidimensionnel, tel que l’interpolation tétraédrale, qui applique les couleurs d’entrée à la transformation. La section suivante décrit comment les tables de choix optimisées sont créées. La section suivante décrit comment interpoler dans les tables de choix optimisées.

Tables de choix éparses

Les imprimantes conventionnelles ont des encres CMJN. Pour étendre la gamme, une approche consiste à ajouter de nouvelles entrées manuscrites au système. Les encres généralement ajoutées sont des couleurs que les encres CMJN ont des difficultés à reproduire. Les choix courants sont l’orange, le vert, le rouge, le bleu, etc. Pour augmenter la « résolution apparente », vous pouvez utiliser des encres avec des teintes différentes, par exemple du cyan clair, du magenta clair, etc. En effet, le périphérique d’imprimante a plus de quatre canaux.

Bien que les imprimantes soient des périphériques de sortie, elles effectuent également la conversion de couleur de l’espace de l’appareil vers un autre espace de couleurs. Dans le cas d’une imprimante CMJN, il s’agit d’une transformation de CMJN en XYZ, ou le « modèle avant » de l’imprimante. En combinant le modèle de transfert avec d’autres transformations, il est possible d’émuler une impression CMJN sur un autre appareil. Par exemple, une imprimante CMJN sur un moniteur RVB rend possible un mécanisme de vérification qui émule une impression de cette imprimante CMJN sur un moniteur. De même, il en va de même pour les imprimantes hi-fi. Une conversion CMYKOG en RVB permet la vérification de l’imprimante CMYKOG sur un moniteur.

L’approche conventionnelle pour implémenter une telle conversion de couleur consiste à utiliser un LUT uniforme. Par exemple, dans un profil ICC pour une imprimante CMYKOG, la spécification ICC impose une étiquette A2B1 qui stocke un LUT uniforme représentant un échantillonnage uniforme dans l’espace d’appareil CMYKOG du modèle avant, qui va de CMYKOG à l’espace de connexion du profil ICC (CIELAB ou CIEXYZ). Le profil de liaison d’appareil ICC permet une transformation directe de l’espace d’appareil CMYKOG vers n’importe quel espace de couleur, y compris un espace d’appareil, également sous la forme d’un LUT échantillonné uniformément dans l’espace CMYKOG. L’échantillonnage n’est jamais effectué avec 256 niveaux (profondeur de bits 8) en raison de l’énorme LUT résultant, sauf dans le cas des appareils monochromes (1 canal). Au lieu de cela, l’échantillonnage avec une profondeur de bits inférieure est utilisé ; certains choix typiques sont 9 (profondeur de bits 3), 17 (profondeur de bits 4), 33 (profondeur de bits 5). Avec le nombre de niveaux inférieur à 256 dans chaque canal, le LUT est utilisé conjointement avec un algorithme d’interpolation pour produire le résultat si un niveau se trouve entre deux niveaux échantillonné.

Bien qu’un LUT uniforme soit conceptuellement simple à implémenter et que l’interpolation sur un LUT uniforme soit généralement efficace, la taille du LUT augmente de façon exponentielle avec la dimension d’entrée. En fait, si d est le nombre d’étapes utilisé dans le LUT uniforme et n le nombre de canaux dans l’espace de couleur source, le nombre de nœuds dans le LUT 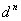. De toute évidence, le nombre de nœuds demande rapidement tellement de stockage en mémoire que même les systèmes informatiques de pointe ont des difficultés à gérer la demande. Pour les appareils avec six ou huit canaux, une implémentation ICC du profil d’appareil nécessite l’utilisation de quelques étapes dans le LUT, parfois même jusqu’à cinq étapes dans la table A2B1 pour conserver le profil en mégaoctets au lieu de gigaoctets. De toute évidence, l’utilisation d’un plus petit nombre d’étapes augmente l’erreur d’interpolation, car il y a maintenant moins d’échantillons. Étant donné que le LUT doit être uniforme, la précision sur l’ensemble de l’espace colorimétrique est dégradée même dans les régions de l’espace où une différence de couleur significative peut être causée par une petite modification de la valeur de l’appareil.

Dans les appareils avec plus de quatre colorants, certains sous-espaces de l’espace de l’appareil sont plus importants que d’autres. Par exemple, dans l’espace CMYKOG, les encres cyan et verte sont rarement utilisées ensemble, car leurs teintes se chevauchent en grande partie. De même, les encres jaunes et oranges se chevauchent en grande partie. Une réduction uniforme du nombre d’étapes peut être vue comme une dégradation globale de la qualité dans l’ensemble de l’espace de couleur, ce qui est quelque chose que vous pouvez vous permettre pour les combinaisons d’encre improbables, mais pas pour les combinaisons probables ou importantes.

Bien qu’un LUT échantillonné uniformément soit simple et efficace pour l’interpolation, il impose des exigences de mémoire énormes à mesure que la dimension augmente. En réalité, alors qu’un appareil peut avoir six ou huit canaux, ils sont rarement utilisés simultanément. Dans la plupart des cas, la couleur d’entrée en transformation de couleur n’a que quelques colorants « actifs » et réside donc dans un espace de couleurs de dimension inférieure. Cela signifie également que l’interpolation peut être effectuée plus efficacement dans cet espace de dimension inférieure, car l’interpolation est plus rapide lorsque la dimension est inférieure.

Par conséquent, l’approche consiste à stratifier l’ensemble de l’espace de l’appareil en sous-espaces de différentes dimensions. Et parce que les dimensions inférieures (celles combinant trois ou quatre colorants) sont plus importantes, en stratifiant l’espace, vous pouvez également appliquer des taux d’échantillonnage différents; c’est-à-dire un nombre différent d’étapes, pour les pièces; augmenter les taux d’échantillonnage pour les dimensions inférieures, les réduire pour les dimensions plus élevées.

Pour corriger les notations, n est le nombre de canaux dans l’espace de couleur source de la transformation de couleur que vous souhaitez échantillonner. Vous pouvez également faire référence à n comme dimension d’entrée, et 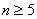, sauf indication contraire.

Les blocs de construction de base sont des unités logiques de dimensions et de tailles d’entrée différentes, au lieu d’un seul LUT uniforme avec la dimension d’entrée n. Pour être plus précis, unLUT est un réseau rectangulaire imposé sur un cube d’unité ; autrement dit, toutes les coordonnées de l’appareil sont normalisées à la plage [0, 1]). si est la dimension d’entrée du lut (notez qu’il n’est pas nécessaire d’être égal à n, bien que 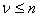soit requis), il se compose de ν grilles d’échantillonnage unidimensionnelles :

Samp i :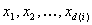

où tous les _{x j}s doivent se trouver dans la plage [0, 1], 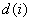représente le nombre d’étapes pour l’échantillonnage du i ième canal qui doit être d’au moins 1, et 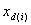doit être égal à 1. En revanche, 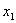Il n’est pas nécessaire d’avoir la valeur 0.

Seuls les deux cas spéciaux suivants de LUT seront définis.

LUT fermé : il s’agit d’un LUT avec l’exigence supplémentaire que pour chaque Samp*_i*, 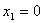, et 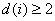. Un LUT fermé uniforme est un LUT fermé qui a le même 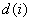pour chaque canal, et les nœuds sont espacés uniformément entre 0 et 1.

Open LUT : il s’agit d’un LUT avec l’exigence supplémentaire qui, pour chaque Samp i, 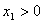. Il est correct d’avoir .

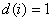L’objectif est de stratifier le cube d’unités [0, 1] n en une collection de LTU fermées et de LUT ouvertes, de sorte que la collection entière couvre le cube d’unités. Il est conceptuellement plus simple d’organiser ces « strates LUT » en fonction de leurs dimensions, de sorte qu’au niveau supérieur :

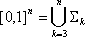
où 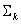est la collection « k -dimensional strata ». Notez que la dimension de strates commence par 3 au lieu de 0 ; c’est-à-dire des points, car l’interpolation de combinaisons de trois colorants peut être gérée sans trop de besoin de mémoire.

Description des strates LUT

Dans cette implémentation :

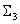1. se compose de LUT fermés avec trois entrées, une parmi chaque combinaison possible de trois colorants choisis parmi les n colorants.

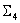2. se compose d’un LUT fermé pour la combinaison CMJN (ou les quatre premiers colorants), ainsi que 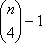luts ouverts pour toutes les autres combinaisons de quatre colorants. En sélectionnant la combinaison CMJN, vous reconnaissez qu’il s’agit d’une combinaison importante.

3. Pour 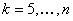, 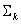se compose de 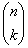open LUTs, un pour chaque combinaison possible de choix k colorants parmi le total de n colorants.

Il reste à spécifier les tailles des LUT. La principale différence entre les luts ouverts et fermés est que les luT ouverts ne se chevauchent pas, et que les luT fermés peuvent se chevaucher aux faces de la limite. Le fait que l’échantillonnage unidimensionnel dans un LUT ouvert ne contienne pas 0 signifie essentiellement qu’un LUT ouvert manque la moitié des faces limites, d’où le nom « open ». Si deux luT ne se chevauchent pas, vous pouvez utiliser un nombre différent d’étapes ou d’emplacements de nœud dans chaque canal. La même chose n’est pas vraie si deux luT se chevauchent. Dans ce cas, si le nombre d’étapes ou les emplacements des nœuds sont différents, un point situé à l’intersection des deux luT reçoit une valeur d’interpolation différente selon le LUT utilisé dans l’interpolation. Une solution simple à ce problème consiste à utiliser un échantillonnage uniforme avec le même nombre d’étapes chaque fois que deux luT se chevauchent. En d’autres termes :

Tous les LUT fermés (tous les LUT à trois colorants et le LUT CMJN dans cette implémentation) doivent être uniformes et avoir le même nombre d’étapes, qui sont indiquées d.

Les deux algorithmes suivants peuvent être utilisés pour déterminer le nombre d’étapes d pour les unités logiques fermées et le nombre d’étapes pour les unités logiques ouvertes.

Algorithme n° 1

Cet algorithme ne nécessite pas d’entrée externe.

Toutes les unités logiques fermées sont uniformes avec un nombre d’étapes .

Toutes les unités logiques ouvertes de la dimension k auront le même nombre d’étapes 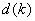dans chaque canal d’entrée, et les nœuds sont également espacés ; autrement dit, pour chaque .

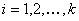Samp i :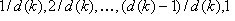

Enfin, spécifiez d et d (k ) dans le tableau 1 suivant. Les trois modes , « preuve », « normal » et « meilleur » sont les paramètres de qualité ICM 2.0. Dans cette implémentation, le mode de preuve a l’encombrement mémoire le plus faible, et le meilleur mode a l’encombrement mémoire le plus élevé.

Pour implémenter cet algorithme, vous devez appeler l’algorithme suivant n°2. Les utilisateurs peuvent spécifier leurs propres emplacements d’échantillonnage, en utilisant les tables comme guide.

Algorithme n°2

Cet algorithme nécessite une entrée externe sous la forme d’une liste d’emplacements d’échantillonnage « importants », mais il est plus adaptatif et peut potentiellement économiser de l’espace mémoire.

L’entrée requise est un tableau de valeurs d’appareil fourni par l’utilisateur. Ces valeurs d’appareil indiquent quelle région de l’espace de couleur de l’appareil est importante ; autrement dit, quelle région doit être échantillonné le plus.

Toutes les unités logiques fermées seront uniformes avec un nombre d’étapes , comme décrit dans Algorithme n°1. Les valeurs de d sont fournies dans le tableau 1.

(a) Uniform Closed LUT

	Mode preuve	Mode Normal	Meilleur mode
D	9	17	33

 

(b) Ouvrir LUT

Dimension d’entrée	Mode preuve	Mode Normal	Meilleur mode
4	5	7	9
5	2	3	3
6	2	3	3
7	2	2	2
8 ou plus	2	2	2

 

Tableau 1 : Tailles LUT utilisées dans l’algorithme

Chaque LUT ouvert peut avoir un nombre différent d’étapes dans chaque canal d’entrée, et les emplacements d’échantillonnage n’ont pas besoin d’être également espacés. Pour une strate LUT ouverte donnée, il existe une combinaison de colorant associée, par exemple, 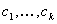, où les 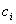s sont des entiers distincts compris entre 1 et n. Il s’agit des indices de canal correspondant aux colorants « actifs » de cette strate.

ÉTAPE 1 : Filtrez le tableau entré de valeurs d’appareil qui ne sont pas contenues dans cette couche. Une valeur d’appareil 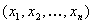est contenu dans les strates, si et uniquement si 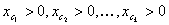tous les autres canaux sont 0. Si l’ensemble filtré a N entrées, laissez

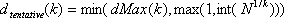
Pour chaque 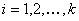, itérer les étapes suivantes 2 à 5 :

ÉTAPE 2 : Si 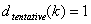, Samp i n’a que 1 point, qui doit être 1.0. Passez au i suivant. Sinon, passez à l’ÉTAPE 3.

ÉTAPE 3 : Triez les exemples filtrés dans l’ordre croissant dans le canal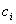

ÉTAPE 4 : Définir la grille d’échantillonnage « provisoire » à l’aide des nœuds

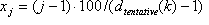
où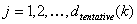

ÉTAPE 5 : Régulariser la grille provisoire pour vous assurer qu’elle est conforme à la monotonicité stricte et qu’elle se termine par 1.0. Étant donné que le tableau est déjà trié, les nœuds de la grille provisoire sont déjà monotoniques nondécasés. Toutefois, les nœuds adjacents peuvent être identiques. Vous pouvez résoudre ce problème en supprimant des nœuds identiques, si nécessaire. Enfin, après cette procédure, si le point de terminaison est inférieur à 1.0, remplacez-le par 1.0.

Notez que l’ÉTAPE 5 est la raison pour laquelle les couches LUT peuvent avoir un nombre d’étapes différent dans chaque canal. Après la régularisation, le nombre d’étapes dans un canal peut être inférieur à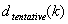

Interpolation

Vous pouvez construire la stratification du cube d’unités en utilisant des strates LUT ouvertes et des strates LUT fermées. Pour effectuer l’interpolation à l’aide de cette « structure LUT éparse », procédez comme suit. Supposons qu’une valeur de périphérique d’entrée donnée .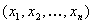

ÉTAPE 1 : Déterminez le nombre de canaux « actifs ». Il s’agit du nombre de canaux autres que zéro. Cela détermine la dimension k des strates à rechercher pour la strate contenante. Plus précisément, la dimension des strates est 3 si le nombre de canaux actifs est 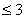Sinon, la dimension des strates est identique au nombre de canaux actifs.

ÉTAPE 2 : Dans 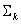, recherchez la strate contenante. Une valeur d’appareil est contenue dans une couche ouverte si tous les canaux correspondant à la strate ont une valeur différente de zéro, et si tous les autres canaux sont zéro. Une valeur d’appareil est contenue dans une couche fermée si chaque canal non représenté par la strate est égal à zéro. Si aucune strate contenante n’est trouvée, il existe une condition d’erreur. Annuler et signaler l’échec. Si une couche contenante est trouvée, passez à l’étape suivante.

ÉTAPE 3 : Si la strate contenante est fermée, l’interpolation au sein de la strate peut être effectuée par n’importe quel algorithme d’interpolation connu. Dans cette implémentation, le choix de l’algorithme est l’interpolation tétraédrale. Si la strate contenante est ouverte et que la valeur de l’appareil se trouve strictement à l’intérieur de la strate, c’est-à-dire,

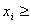premier nœud dans i ième canal

où i est un index de canal pour la strate, puis l’algorithme d’interpolation standard, tel que l’interpolation tétraédrale, fonctionne.

Si 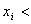premier nœud dans i th canal pour certains i, la valeur de l’appareil tombe dans l'« écart » entre la strate et les sous-espaces de dimension inférieure. Ce MOI n’est pas concerné par un algorithme d’interpolation en soi. Par conséquent, n’importe quel algorithme d’interpolation peut être utilisé pour interpoler dans cette « lacune », bien que l’algorithme préféré soit l’interpolation transfinite suivante.

L’architecture du module d’interpolation est illustrée dans les deux parties de la figure 1.

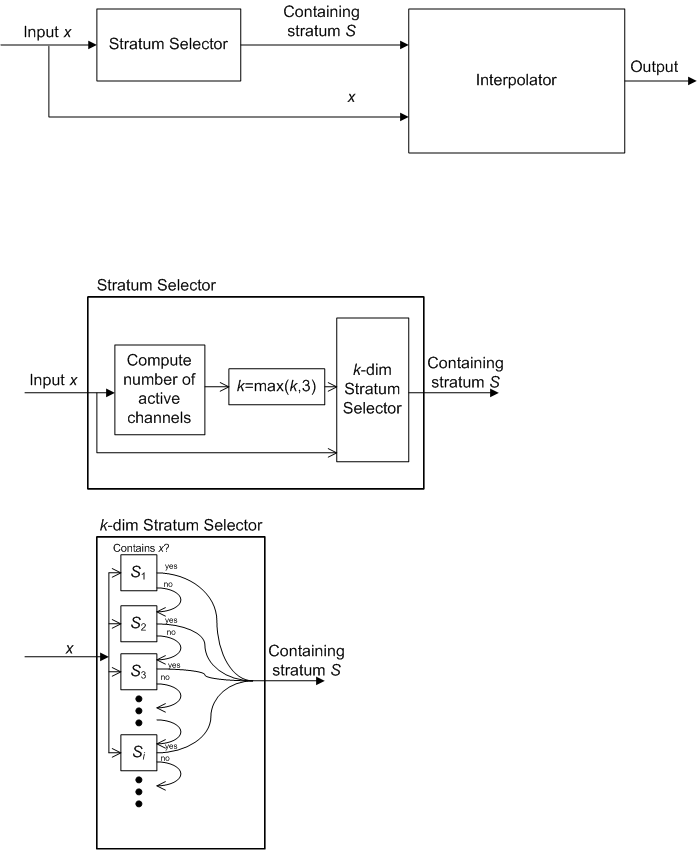
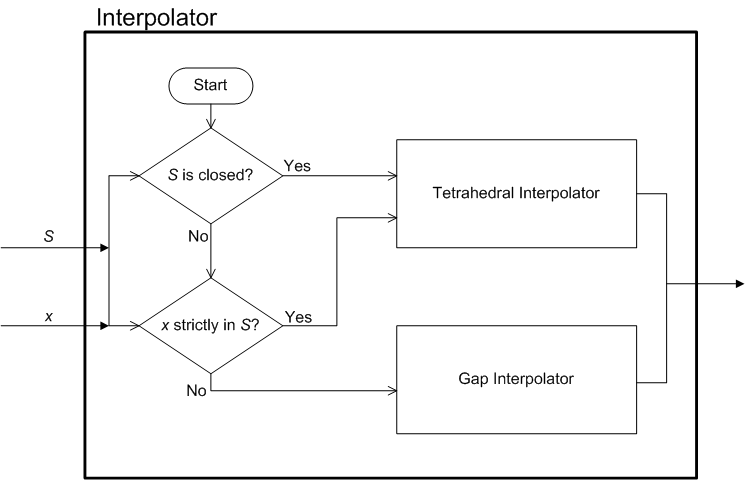
Figure 1 : Architecture du module d’intepolation

Comme expliqué précédemment, cet algorithme est capable d’effectuer un échantillonnage relativement dense dans les régions de l’espace de l’appareil qui contiennent une combinaison importante de colorants, tout en réduisant la taille totale des LUT nécessaires. Le tableau suivant présente une comparaison du nombre de nœuds nécessaires pour l’implémentation LUT éparse (à l’aide de l’algorithme n°1 et du mode normal) et de l’implémentation uniforme LUT correspondante.

Nombre de canaux d’entrée	LUT partiellement alloué	LUT uniforme
5	142498	1419857
6	217582	24137567
7	347444	410338673
8	559618	6975757441

 

Interpolation dans un cube d’unité

Une étape de base dans le cas d’une grille rectangulaire est l’interpolation dans une cellule englobante. Pour un point d’entrée, vous pouvez facilement déterminer la cellule englobante. Dans une grille rectangulaire, la valeur de sortie à chacun des sommets (points d’angle) de la cellule englobante est spécifiée. Il s’agit également des seules conditions limites (BC) auxquelles un interpolant doit satisfaire : l’interpolant doit passer par tous ces points. Notez que ces conditions limites se trouvent sur des points « discrets », dans ce cas les 2n points d’angle de la cellule, où n est la dimension de l’espace de couleurs.

Il est utile de formaliser le concept de conditions limites avant de passer à autre chose. Pour tout sous-ensemble S de la limite de la cellule englobante (cube d’unité dans n dimensions), une condition de limite sur S est une spécification d’une fonction BC : S → Rm, où m est la dimension de sortie. En d’autres termes, un interpolant, qui peut être nommé Interp : [0,1]n→ Rm, est requis pour satisfaire : Interp(x) = BC(x) pour tous les x dans S.

Dans le scénario standard d’interpolation sur le cube d’unité, S est l’ensemble de points discrets qui sont les 2n sommets du cube.

Vous pouvez maintenant généraliser les conditions limites pour résoudre les problèmes décrits précédemment et fournir un nouvel algorithme d’interpolation dans le cube d’unité. Au lieu d’autoriser uniquement des points de limite discrets, des conditions limites peuvent être imposées à une face limite entière du cube. Les hypothèses précises sont les suivantes :

(a) Le point vn =(1,1,...,1) est spécial et seule une condition de limite discrète est autorisée. En d’autres termes, aucune condition de limite continue ne peut être imposée aux n faces limites xi=1 (i=1,...,n).

(b) Pour chacune des n faces de limite restantes xi=0 (i=1,...,n), une condition limite peut être imposée à l’ensemble de la face, avec la condition de compatibilité selon laquelle si deux faces se croisent, les conditions limites des visages doivent convenir de l’intersection.

(c) Tous les sommets non contenus dans les visages avec condition limite auront une condition limite individuelle (discrète).

Vous pouvez faire référence à une condition de limite discrète en tant que données finies et à une condition de limite continue en tant que données transfinites pour discuter de l’interpolation sur les données finies et transfinites.

Tout d’abord, passez en revue l’interpolation tétraédrique standard (comme celle utilisée dans le brevet de Sakamoto) qui permet de définir les notations pour cette formulation particulière du problème. On sait que le cube d’unité [0,1]n peut être subdivisé en n! tétraèdre, paramétré par l’ensemble de permutations sur n symboles. Plus spécifiquement, chacun de ces tétraèdre est défini par les inégalités

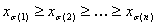
où σ:{1,2,..,n}→{1,2,...,n} est une permutation de « symboles » 1, 2, ..., n, c’est-à-dire un mappage bijectif de l’ensemble de n symboles. Par exemple, si n = 3 et σ = (3, 2, 1), ce qui signifie σ(1)=3, σ(2)=2, σ(3)=1, le tétraèdre correspondant est défini par z≥y≥x, où la notation commune x, y, z est utilisée pour x1, x2, x3. Notez que ces tétraèdres ne sont pas disjoints les uns des autres. Aux fins de l’interpolation, les points situés sur une face commune de deux tétraèdres distincts auront la même valeur d’interpolation, quel que soit le tétraèdre utilisé dans l’interpolation. Néanmoins, dans le scénario standard d’interpolation sur des points finis, pour un point d’entrée donné (x1, ..., xn), déterminez d’abord le tétraèdre dans lequel il se trouve, ou de façon équivalente, la permutation correspondante σ, puis l’interpolant tétraédral est défini comme étant

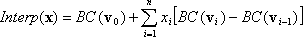
où 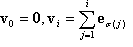pour i=1, ..., n et e1, ..., en sont les vecteurs de base standard. Avant de passer à la généralisation, notez que v0, v1, ..., vn sont les sommets du tétraèdre et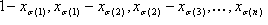

Pour le cas général des contrôleurs de bord sur les faces limites, vous pouvez utiliser le concept de projection barycentrique. Comme précédemment, pour un point d’entrée donné (x1, ..., xn), déterminez d’abord dans quel tétraèdre il se trouve, ou de manière équivalente, la permutation correspondante σ. Effectuez ensuite une série de projections barycentriques, comme suit. La première projection 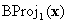envoie le point au plan 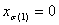Sauf si 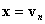Dans ce cas, il n’est pas modifié. La définition précise de la carte BProj est définie comme suit :

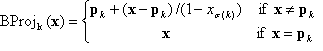
avec 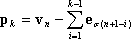et k = 1, 2, ..., n.

Dans le cas 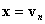, vous pouvez arrêter, car BC est défini à vn par l’assomption (a). Dans le cas 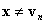, il est clair que 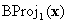a le composant σ(1)th annihilé. En d’autres termes, il se trouve sur l’une des faces limites. Soit il se trouve sur une face sur laquelle BC est défini, auquel cas vous pouvez arrêter, soit vous effectuez une autre projection barycentrique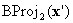 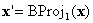Et si 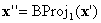est sur un visage sur lequel BC est défini, vous pouvez arrêter ; sinon, effectuez une autre projection 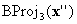Étant donné que chaque projection annihile un composant, la dimension effective diminue. Vous savez donc que le processus doit s’arrêter. Dans le pire des cas, vous effectuez n projections jusqu’à la dimension 0, c’est-à-dire des sommets sur le cube, qui, selon l’hypothèse (c), vous savez que BC sera défini sur.

En supposant que K projections ont été effectuées, avec

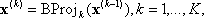
x(0)= x, le point d’entrée et BC est défini à x(k). Ensuite, déroulez les projections en définissant une série de vecteurs de sortie :

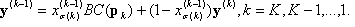
où 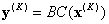, et vous obtenez enfin la réponse

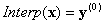
Exemple pratique

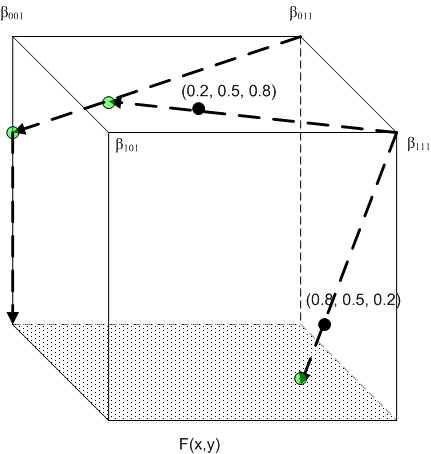
Figure 2 : Exemple de travail

Considérez la situation illustrée à la figure 2, où n = 3, m = 1, et vous avez les contrôleurs de base suivants :

a) Quatre BCs discrets sur les sommets

(0, 0, 1): β001

(0, 1, 1): β011

(1, 0, 1): β101

(1, 1, 1): β111

(b) Bc continue sur le visage x3=0 : F(x1, x2)

Calcul n°1 : point d’entrée x = (0,8, 0,5, 0,2). Le tetraèdre englobant est associé à la permutation <1, 2, 3>.

1ère projection :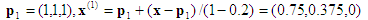

C’est déjà sur le visage x3=0, vous pouvez donc vous arrêter. La substitution vers l’arrière donne alors

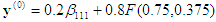qui est la réponse.

Calcul n°2 : point d’entrée x = (0,2, 0,5, 0,8). Le tétraèdre englobant est associé à la permutation <3, 2, 1>.

1ère projection :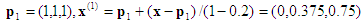

2e projection :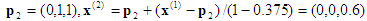

3e projection : 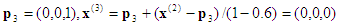, qui est sur la face x3=0. La substitution vers l’arrière donne alors

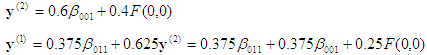
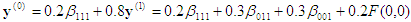, qui est la réponse finale.

Applications

(a) Interpolation séquentielle de type tetraédral

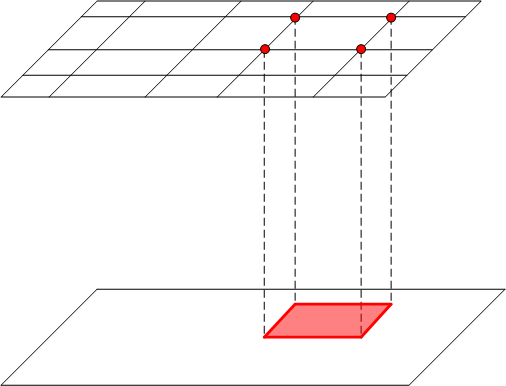
Figure 3 : Interpolation quadriédrale séquentielle

Reportez-vous à la figure 3. Pour interpoler entre deux plans sur lesquels des grilles incompatibles ont été imposées, considérez une cellule englobant un point P donné illustré dans la figure. Les sommets « supérieurs » de la cellule proviennent directement de la grille dans le plan supérieur. Les sommets dans la face inférieure ne sont pas compatibles avec la grille dans le plan inférieur, de sorte que la face entière est traitée comme ayant une bc avec des valeurs obtenues par interpolation sur la grille dans le plan inférieur. Il est alors clair que cette configuration répond aux hypothèses (a), (b) et (c) ci-dessus, et vous pouvez appliquer l’algorithme d’interpolation.

Il est également clair que l’algorithme a réduit la dimension du problème d’interpolation de 1, car le résultat est une combinaison linéaire de valeurs aux sommets dans la grille supérieure et l’interpolation dans le plan inférieur, qui a une dimension moins 1. Si une configuration de plan de sandwich similaire existe dans le plan inférieur, vous pouvez appliquer la procédure dans ce plan, en réduisant la dimension de 1. Cette procédure peut continuer jusqu’à ce que vous atteigniez la dimension 0. Cette cascade de projections et d’interpolations peut être appelée « Interpolation séquentielle de type tetraédral ».

(b) Interpolation d’écart

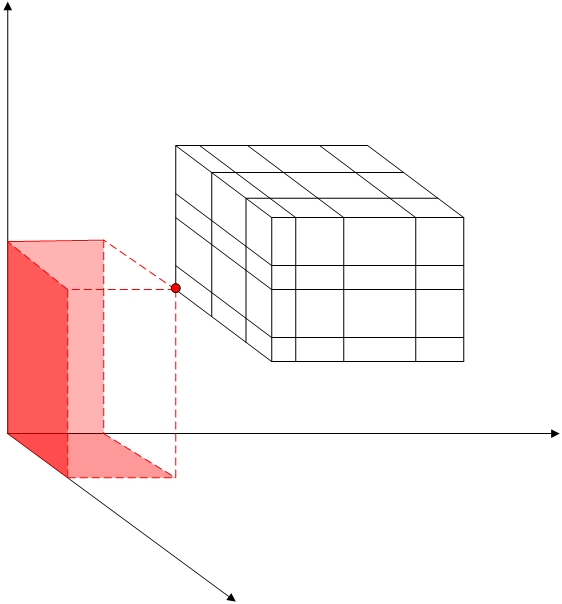
Figure 4 : Interpolation d’écart

Il s’agit d’une grille imposée sur un cube se trouvant strictement à l’intérieur du quadrant positif. Le cube lui-même a une grille, et chaque plan de coordonnées a des grilles qui ne sont pas nécessairement compatibles. L'« écart » entre le cube et les plans de coordonnées a une section croisée « en forme de L » et n’est pas accessible aux techniques standard. Toutefois, avec la technique introduite ici, vous pouvez facilement introduire des cellules qui couvrent cette lacune. La figure 4 illustre l’un de ces éléments. Les grilles sur les plans de coordonnées prennent en charge l’interpolation qui fournit les BC nécessaires pour toutes les faces inférieures de la cellule, avec un sommet restant dont bc est fourni par le coin inférieur du cube.

Note finale sur l’implémentation

Dans l’application réelle, le « cube d’unité » qui est le paramètre de base de l’algorithme est extrait de lattics plus grands, et les valeurs aux sommets peuvent nécessiter un calcul coûteux. D’un autre côté, il est également clair que l’interpolation de la forme de l’unité ne nécessite que les valeurs au niveau des sommets du quadrièdre, qui est un sous-ensemble de tous les sommets du cube d’unité. Par conséquent, il est plus efficace de mettre en œuvre ce qu’on peut appeler une « évaluation différée ». Dans une implémentation logicielle de l’algorithme précédent, il est courant d’avoir une sous-routine qui prend le cube d’unité et les valeurs à ses sommets comme entrée. L’évaluation différée signifie qu’au lieu de transmettre les valeurs au niveau des sommets, les informations nécessaires à l’évaluation des valeurs des sommets sont passées, sans réellement effectuer l’évaluation. À l’intérieur de la sous-routine, l’évaluation réelle de ces valeurs ne sera effectuée que pour les sommets qui appartiennent au tétraèdre englobant, une fois le tétraèdre englobant déterminé.

Table de recherche à utiliser avec des appareils sources RVB virtuels à plage dynamique élevée

Dans le cas où une transformation est construite avec un appareil source modélisé comme un appareil RVB virtuel, il est possible que les valeurs de colorant source soient négatives ou supérieures à unity (1.0). Lorsque cela se produit, l’appareil source est appelé avoir une plage dynamique élevée (HDR). Une attention particulière est apportée à ce cas.

Dans le cas de transformations HDR, les valeurs minimales et maximales de chaque canal colorant peuvent être déterminées à partir de la limite de la gamme de l’appareil. En utilisant ces valeurs, une mise à l’échelle simple pour chaque canal colorant est appliquée afin que les valeurs de colorant égales au colorant minimal soient converties en 0,0, et que les valeurs de colorant égales au colorant maximal soient converties en 1,0, avec une mise à l’échelle linéaire des valeurs entre pour mapper linéairement entre 0,0 et 1,0.

ICCProfileFromWCSProfile

Étant donné que l’objectif main de cette fonctionnalité est de prendre en charge les versions antérieures à Vista de Windows, vous devez générer des profils ICC version 2.2 comme défini dans la spécification ICC.1:1998-09. Dans certains cas (voir le tableau suivant « Mappage de classe de profil de base de l’appareil à la classe de profil ICC »), vous pouvez créer une matrice ou un profil ICC basé sur TRC à partir d’un profil WCS. Dans d’autres cas, le profil de la CPI se compose de luts. Le processus suivant décrit comment créer les unités logiques AToB et BToA. Bien sûr, les profils icc ont d’autres domaines aussi. Certaines données peuvent être dérivées du profil WCS. Pour les autres données, vous devez développer des valeurs par défaut intelligentes. Le droit d’auteur sera attribué à Microsoft ; puisque c’est la technologie Microsoft qui est utilisée pour créer les LUT.

Cette conception doit fonctionner pour tous les types de modèles d’appareils, y compris les plug-ins. Tant que le plug-in a un modèle d’appareil de base associé, le type d’appareil sous-jacent peut être déterminé.

La partie difficile de la création d’un profil ICC consiste à créer les tables de recherche AToB et BToA. Ces tableaux sont mappés entre l’espace de l’appareil, par exemple RVB ou CMJN, et l’espace de connexion de profil (PCS), qui est une variante de CIELAB. Cela est fondamentalement identique au processus de gestion des couleurs utilisé dans la transformation CITE pour mapper de l’espace de l’appareil à l’espace de l’appareil. Toutefois, vous devez disposer des informations suivantes pour effectuer la transformation.

1. Référencer les conditions d’affichage du PCS.

2. Référencer la gamme PCS.

3. Modèle d’appareil qui convertit les valeurs PCS et la colorimétrie.

Le profil WCS et sa CAM associée sont fournis en tant que paramètres. Il existe deux modèles d’appareil de base qui effectuent une conversion entre la colorimétrie et l’encodage PCS. La raison pour laquelle vous en avez besoin est expliquée ci-dessous.

1. Vous pouvez obtenir les conditions d’affichage de référence pour le PCS à partir de la spécification du format de profil ICC. Les informations fournies dans la spécification du format de profil ICC sont suffisantes pour calculer toutes les données requises pour initialiser la CAM utilisée par le CMS. Par souci de cohérence et de flexibilité, ces informations sont stockées dans un profil de couleur WCS.

2. Vous pouvez également utiliser un profil WCS pour stocker des exemples qui définissent la gamme de référence du PCS. Le système de gestion des couleurs CITE (CMS) offre deux façons de créer des limites de gamme. L’une consiste à échantillonner l’espace complet de l’appareil et à utiliser le modèle d’appareil pour créer des valeurs de mesure. La deuxième méthode consiste à utiliser des échantillons mesurés à partir du profil pour créer une limite de gamut de référence. Étant donné que la gamme du PCS ICC est trop grande pour en faire une gamme de référence utile, la première méthode est inappropriée. Mais la deuxième méthode est une approche flexible basée sur des profils. Pour redéfinir la gamme PCS de référence, vous pouvez modifier les données de mesure dans le profil d’appareil PCS.

3. Le PCS ICC est une modélisation d’un appareil idéal. En créant un modèle du PCS en tant qu’appareil réel, vous pouvez tirer parti du processus de gestion des couleurs utilisé dans la CMM intelligente. La création d’un modèle d’appareil à partir de la colorimétrie vers l’encodage PCS est simple. Il vous suffit de mapper entre les vraies valeurs colorimétriques et les valeurs encodées PCS. Étant donné que l’interface CMS pour les modèles d’appareil prend uniquement en charge les valeurs XYZ, vous devrez peut-être également mapper xyz et LAB. Il s’agit d’une transformation bien connue. Ce modèle est décrit dans le document 2.2.02 « Modèles d’appareil de base » dans les sections 7.9 et 7.10.

Vous devrez peut-être effectuer un mappage de gamut si la gamme de l’appareil est supérieure à la gamme du PCS. Les MGM de base peuvent être utilisés à cette fin. Notez qu’un profil ICC correctement créé comporte des tables de recherche pour les intentions colorimétriques, perceptuelles et de saturation relatives, bien qu’elles puissent toutes pointer vers le même LUT en interne.

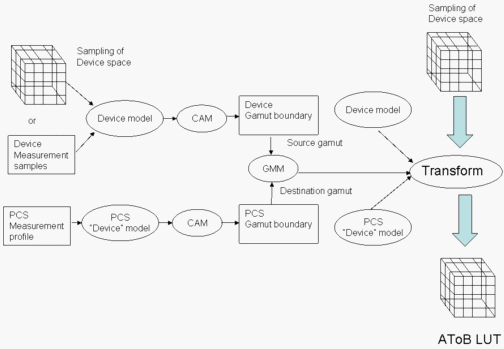
Figure 5 : Création d’un LUT AToB

Ce processus est illustré dans la figure 5. Tout d’abord, le modèle d’appareil est initialisé à partir des données du profil DM. Ensuite, construisez une limite de gamme d’appareils comme suit. Un échantillonnage des données du modèle d’appareil est exécuté via le modèle d’appareil pour obtenir des données colorimétriques. Les données colorimétriques sont exécutées via la CAM pour créer des données d’apparence. Les données d’apparence sont utilisées pour créer la limite de la gamme d’appareils.

Ensuite, utilisez les données du profil de mesure PCS de référence pour créer une limite de gamut pour le PCS.

Utilisez les deux limites de gamut que vous venez de créer pour initialiser un GMM. Ensuite, utilisez le modèle d’appareil, le GMM et le modèle d’appareil PCS pour créer une transformation. Exécutez un échantillonnage de l’espace d’appareil via la transformation pour créer un LUT AToB.

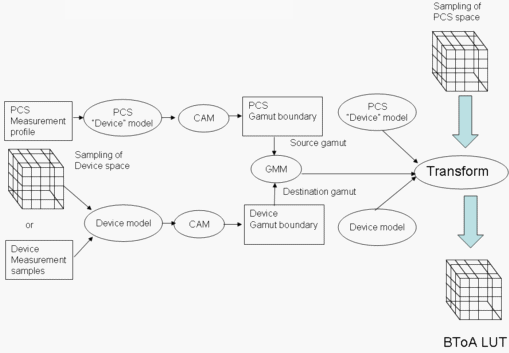
Figure 6 : Création d’un LUT BToA

La figure 6 illustre la création du LUT BToA. Cela est presque identique à la création d’un LUT AToB, avec les rôles de source et de destination échangés. En outre, vous devez échantillonner la gamme PCS complète pour créer le LUT.

Notez que étant donné que le CAM (CIECAM02 dans WCS) est impliqué dans le processus, l’adaptation chromatique entre le point blanc du média et le point blanc PCS (mandaté par icc comme étant celui de D50) est effectuée de manière transparente par le CAM.

Appareils RVB virtuels HDR

Une attention particulière doit être prise en compte lors de la génération de profils pour les appareils RVB virtuels HDR ; c’est-à-dire les appareils pour lesquels les valeurs de colorant peuvent être inférieures à 0,0 ou supérieures à 1,0. Dans la génération du LUT ATOB, un plus grand ensemble de LUT d’entrée 1D est généré. Les valeurs de colorant sont mises à l’échelle et décalées à la plage 0 .. 1 en utilisant les valeurs minimales et maximales de colorant dans le profil WCS.

Étant donné que l’espace colorant des appareils HDR n’est probablement pas complètement rempli, une prise en charge spéciale est fournie dans le LUT 3D pour l’étiquette. Afin de gérer les couleurs dans la région peu peuplée, les colorants sont recodés afin d’obtenir une extrapolation au-delà de 0,0 et 1,0. La plage utilisée est -1 .. +4.

En raison de la mise à l’échelle appliquée pour le LUT 3D, un ensemble de luts de sortie 1D est créé pour mapper le résultat à la plage 0 .. 1.

Plusieurs PCS

La CPI a conclu qu’un PCS n’était pas suffisamment souple pour répondre à toutes les utilisations prévues d’un CMS. Dans la version 4 de la spécification de profil, l’ICC a précisé qu’il existe en fait deux encodages PCS. Un est utilisé pour les intentions colorimétriques; une autre est utilisée pour l’intention perceptuelle. (Aucun PCS n’est spécifié pour l’intention Saturation. La CPI a laissé cette partie ambiguë.) Le PCS colorimétrique a une légèreté minimale et maximale spécifiée, mais les valeurs de chroma et de teinte sont comprises à environ ± 127. Ce PCS ressemble à un prisme rectangulaire. Comme mentionné précédemment, le volume de PCS perceptuel ressemble à la gamme d’une imprimante à jet d’encre.

Les deux PCS ICC ont également deux encodages numériques différents. Dans le PCS perceptuel, une valeur de zéro représente une légèreté de zéro. Dans le PCS colorimétrique, la valeur zéro représente la légèreté minimale du PCS, qui est supérieure à zéro. Vous pouvez résoudre ce problème en ayant un modèle d’appareil différent pour chacun des encodages PCS.

Mappage de gamuts

Pour créer les unités logiques AToB dans un profil ICC, vous mappez de la gamme d’appareils à l’espace PCS approprié. Pour créer les unités logiques BToA, vous mapper de l’espace PCS à la gamme d’appareils. Le mappage des unités logiques AToB est assez similaire à celui utilisé dans un CMS basé sur les mesures. Pour le PCS perceptuel, mappez la gamme plausible de l’appareil à la limite de la gamme PERCEPTual PCS, en utilisant le découpage ou la compression pour toutes les couleurs hors gamut. Pour les intentions colorimétriques, vous devrez peut-être découper la légèreté, mais les valeurs de chroma et de teinte vont toutes s’adapter à la gamme colorimétrique PCS.

Le mappage des unités logiques BToA est un peu différent. Les intentions colorimétriques sont toujours faciles; il vous suffit de découper les valeurs PCS sur la gamme de l’appareil. Toutefois, l’ICC exige que toutes les valeurs PCS possibles soient mappées à une valeur d’appareil, et pas seulement à celles figurant dans la gamme de référence du PCS perceptuel. Par conséquent, vous devez vous assurer que les MGM peuvent gérer les couleurs sources qui se trouvent en dehors de la gamme de référence. Pour ce faire, vous pouvez découper ces couleurs sur la limite de la gamme de l’appareil.

Mappage d’appareil de base à classe de profil ICC

Type d’appareil de référence	Classe de profil ICC	Remarque
Périphérique de capture RVB	Périphérique d’entrée (« scnr »)	PCS est CIELAB. AToB0Tag est Appareil vers PCS avec intention colorimétrique relative.
CRT, moniteur LCD	Périphérique d’affichage (« mntr »)	PCS est CIEXYZ. Consultez les rubriques suivantes pour la conversion de modèle.
Projecteur RVB	Espace de couleur (« espace »)	PCS est CIELAB.
Imprimante RVB et CMJN	Périphérique de sortie (« prtr »)	PCS est CIELAB.
Appareil virtuel RVB (cas non HDR)	Périphérique d’affichage (« mntr »)	PCS est CIEXYZ.
Appareil virtuel RVB (cas HDR)	Espace de couleur (« espace »)	PCS est CIELAB.

 

La conversion des profils d’analyse n’implique pas la création de luts, mais consiste plutôt à créer une matrice ou un modèle TRC. Le modèle utilisé dans ICC est légèrement différent de celui utilisé dans la modélisation WCS CRT ou LCD en ce que le terme « correction noire » est manquant. Plus précisément :

Modèle WCS :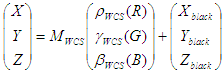

Modèle ICC :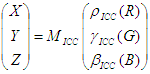

La conversion du modèle WCS en modèle ICC s’effectue comme suit.

Définissez de nouvelles courbes :

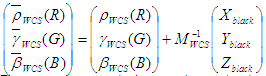
Il ne s’agit pas de courbes de reproduction de tonalités, car elles ne mappent pas 1 à 1. Une normalisation y parvient. Les définitions finales du modèle ICC sont les suivantes :

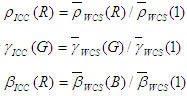
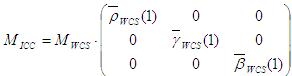
Pour les appareils virtuels RVB non HDR, vous générez également un profil ICC d’affichage pour l’efficacité de l’espace. Dans ce cas, la matrice tristimulus M ICC peut être obtenue directement à partir des primaires du profil WCS sans la conversion de modèle ci-dessus. Une dernière remarque, mais importante, est que cette matrice tristimulus doit être adaptée chromatiquement à D50 pour se conformer à la spécification ICC du PCS. En d’autres termes, les entrées sur chaque ligne de la matrice à encoder dans le profil ICC doivent correspondre respectivement à 96,42, 100 et 82,49. Dans l’implémentation actuelle, l’adaptation chromatique est effectuée par CAT02, qui est également la transformation d’adaptation chromatique utilisée dans CAM02.

Black Preservation et Black Generation

L’implémentation de la préservation des noirs est liée à la génération du canal noir dans les appareils qui prennent en charge un canal noir. Pour ce faire, des informations sur chaque couleur de source sont collectées pour permettre aux modèles d’appareils qui prennent en charge un canal noir de déterminer la meilleure façon de définir le canal noir sur la sortie. Bien que la conservation des noirs soit pertinente pour les transformations de couleur qui se convertissent d’un appareil à canal noir à un autre, la génération noire est implémentée pour toutes les transformations impliquant un appareil de destination de canal noir.

Les informations de canal noir sont enregistrées dans une structure de données appelée BlackInformation. La structure BlackInformation contient une valeur booléenne indiquant si la couleur contient uniquement du colorant noir et une valeur numérique indiquant le degré de « noirceur » appelé « poids noir ». Pour les appareils sources qui prennent en charge un canal noir, le poids noir est le pourcentage de colorant noir dans la couleur source. Pour les appareils sources qui ne contiennent pas de canal noir, le poids noir est calculé à l’aide des autres colorants et de la valeur d’apparence. Une valeur appelée « pureté de la couleur » est calculée en prenant la différence entre la valeur maximale de colorant et la valeur minimale de colorant divisée par la valeur maximale du colorant. Une valeur appelée « légèreté relative » est calculée en prenant la différence entre la légèreté de la couleur et la légèreté minimale pour l’appareil de destination divisée par la différence entre la luminosité minimale et la luminosité maximale pour l’appareil de destination. Si l’appareil source est un appareil additif (moniteur ou projecteur), le poids noir est déterminé comme étant de 1,0 moins la pureté des couleurs multipliée par la légèreté relative. Par exemple, si l’appareil source est un moniteur RVB, la valeur maximale et la valeur minimale de R, G et B pour chaque couleur sont calculées et le poids noir est déterminé par la formule :

BW = (1,0 – (max(R,G,B) – min(R,G,B)) / max(R, G, B)) * légèreté relative

Si l’appareil source prend en charge la coloration soustractive, par exemple une imprimante CMY, les colorants individuels doivent être « complétés » (soustraits de 1.0) avant d’être utilisés dans la formule précédente. Par conséquent, pour une imprimante CMY, R = 1.0 – C, G = 1.0 – M et B = 1.0 – Y.

Les informations noires pour chaque couleur traitée par la transformation de couleur sont déterminées pendant le processus de traduction de couleur. Les informations en noir uniquement sont déterminées si la conservation des noirs est spécifiée. Le poids noir est toujours déterminé si le modèle d’appareil de destination prend en charge un colorant noir. Les informations noires sont transmises au modèle d’appareil de destination via la méthode ColorimetricToDeviceColorsWithBlack , qui utilise le LUT résultant.

Notez que, en raison de l’optimisation de la transformation de couleur, le processus ci-dessus se produit uniquement lors de la création de la LUT de transformation optimisée, et non pendant l’exécution de la méthode TranslateColors.

Optimisation des transformations avec plus de trois canaux sources

La taille de la transformation optimisée est déterminée par plusieurs facteurs : le nombre de canaux de couleur dans l’appareil source, le nombre d’étapes dans le tableau pour chaque canal de couleur source et le nombre de canaux de couleur dans l’appareil de sortie. La formule pour déterminer la taille de la table de transformation est la suivante :

Size = Nombre d’étapes par source de canal _{\ device(Number\ of\ channels\ in\ source\ device)} x nombre de canaux dans l’appareil de sortie

Comme vous pouvez le voir, la taille de la table augmente de façon exponentielle en fonction du nombre de canaux dans l’appareil source. De nombreux appareils sources prennent en charge trois canaux de couleur, par exemple rouge, vert et bleu. Toutefois, si un appareil source prend en charge quatre canaux, tels que CMJN, la taille de la table et le temps nécessaire pour construire la table augmentent d’un facteur du nombre d’étapes. Dans un CMS basé sur les mesures où les transformations sont construites « à la volée », cette fois peut bien être inacceptable.

Pour réduire le temps nécessaire à la construction de la table de conversion de couleurs, il est possible de tirer parti de deux faits. Tout d’abord, alors que l’appareil source peut prendre en charge plus de trois canaux de couleur, l’espace de couleur intermédiaire indépendant du périphérique (CIECAM02 Ja _C b _C ) n’a que trois canaux de couleur. Deuxièmement, la partie la plus longue du traitement n’est pas la modélisation de l’appareil (conversion des coordonnées de couleur d’appareil en valeurs tristimulus), mais le mappage de la gamme. À l’aide de ces faits, vous pouvez construire une table de conversion de couleurs préliminaire qui convertit les couleurs dans l’espace de couleurs indépendant de l’appareil par le biais des étapes de mappage de gamut et, enfin, via le modèle de couleur d’appareil de sortie. La construction de cette table est de dimension 3. Ensuite, nous construisons la table de conversion de couleur finale de quatre dimensions en convertissant les combinaisons de couleurs sources en espace intermédiaire indépendant de l’appareil, puis, à l’aide de la table de conversion de couleur préliminaire, terminez la conversion en espace colorimétrique du périphérique de sortie. Ainsi, vous réduisez du calcul (nombre d’étapes dans la table de choix) _{le nombre\ de\ canaux} de mappage de gamuts au nombre d’étapes dans la table intermédiaire ₃ calculs de mappage de gamuts. Même si vous devez effectuer un nombre d’étapes dans le nombre de canaux ( table de choix) _{nombre\ de\ calculs} de la modélisation d’appareil et des recherches de tables tridimensionnelles, cela reste beaucoup plus rapide que le calcul d’origine.

Le processus précédent fonctionne correctement, à condition qu’il n’y ait pas besoin d’informations à transmettre entre le modèle d’appareil source et tout autre composant de la transformation de couleur. Toutefois, si le dispositif de sortie et le dispositif source prennent tous deux en charge un colorant noir et que le colorant noir source est utilisé pour déterminer le colorant noir de sortie, le processus ne parvient pas à communiquer correctement les informations sur le noir source. Un autre processus consiste à construire une table de conversion de couleurs préliminaire qui convertit les couleurs dans l’espace de couleurs indépendant de l’appareil par le biais des étapes de mappage de gamut uniquement. Ensuite, construisez la table de conversion de couleur finale de la dimension quatre en procédant comme suit : a) convertissez les combinaisons de couleurs sources en espace intermédiaire indépendant du périphérique, b) effectuez les étapes de mappage de gamut en interpolant dans la table de couleurs préliminaire au lieu d’appliquer les processus de mappage de gamut réels, et c) utilisez les valeurs résultantes des étapes de mappage de gamut et des informations de canal noir source pour calculer les colorants de périphérique de sortie à l’aide du modèle d’appareil de sortie. Ce processus peut également être utilisé quand des informations sont transférées entre les modèles d’appareil source et de sortie, même s’il n’y a pas de canal noir ; par exemple, si les deux modules sont implémentés avec une architecture de plug-in qui permet l’échange de données entre les modules.

Les deux processus précédents peuvent être utilisés pour améliorer efficacement le temps nécessaire à la construction de la table de transformation de couleurs à quatre dimensions.

CheckGamut

L’ICM appelle CreateTransform et CreateMultiProfileTransform prennent un mot de valeurs d’indicateur, dont l’une est ENABLE_GAMUT_CHECKING. Lorsque cet indicateur est défini, CITE doit créer la transformation différemment. Les étapes initiales sont les mêmes : les cartes d’accès client source et de destination doivent être initialisées, puis les descripteurs de limites de gamut source et de destination doivent être initialisés. Quelle que soit l’intention spécifiée, le GMM CheckGamut doit être utilisé. Le GMM CheckGamut doit être initialisé à l’aide des modèles d’appareil source et de destination et des descripteurs de limites de gamut. Toutefois, la transformation doit ensuite créer une transformation tronquée comprenant le modèle d’appareil source, la cam source, toutes les machines gmms intermédiaires et checkGamut GMM. Cela garantit que les valeurs delta J, delta C et delta h sorties par checkGamut CMM deviennent les valeurs résultantes finales.

La signification de CheckGamut est claire lorsqu’il n’y a que deux profils d’appareil dans la transformation. Lorsqu’il existe plus de deux profils d’appareil et plus de deux MMM, CheckGamut indique si les couleurs qui ont été transformées via le premier modèle d’appareil et toutes les GMM sauf le dernier sont comprises dans la gamme de l’appareil de destination.

Rubriques connexes

Concepts de base de la gestion des couleurs

Schémas et algorithmes du système de couleurs Windows