Algorithmes et schéma de profil de modèle de mappage de couleur WCS

• Vue d'ensemble
• Architecture de profil de modèle de carte gamut
• Génération de la limite de gamut
• Schéma GMMP
• Éléments de schéma GMMP
• GamutMapModel
  • Espace de noms
  • Version
  • Documentation
  • Type DefaultBaselineGamutMapModel
  • PlugInGamutMapType
  • ExtensionType
• Algorithmes de base GMMP
• Alignement des axes neutres
  • Différence de couleur minimale (MinCD)
  • BasicPhoto
  • Vue d'ensemble
  • Cas de l’interpréteur de commandes à gamut unique
  • Amélioration du noir
  • Le cas des interpréteurs de commandes à double gamut
  • Raisons des modifications apportées aux recommandations TC8-03 du CIE
  • Mappage de teintes
• Description de la limite de gamut et algorithmes d’interpréteur de commandes de gamuts
  • Triangulation de la limite de gamut
  • Éléments de ligne de limite
  • Opération Gamut : CheckGamut
  • Plan de teinte complet : Intersection
  • Opération gamut : CheckGamut (suite)
  • Mappage de la gamme de différences de couleurs minimales
  • Lissage des teintes
  • Définition des valeurs primaires et secondaires dans la description de la limite de gamut
  • Définition de l’axe neutre dans la description de la limite de gamut
• Rubriques connexes

Vue d’ensemble

Ce schéma est utilisé pour spécifier le contenu d’un profil de modèle de carte gamut (GMMP). Les algorithmes de base associés sont décrits dans la rubrique suivante.

Le schéma GMMP de base se compose d’informations d’en-tête courantes, d’une référence facultative à un plug-in Gamut Map Model préféré et de balises d’extension.

En outre, le GMMP fournit des informations explicites sur le modèle de carte gamut ciblé et fournit une stratégie sur le modèle de carte gamut de référence de secours à utiliser si le modèle ciblé n’est pas disponible. Le schéma peut inclure des informations d’extension privées, mais n’inclut aucune autre information superflue.

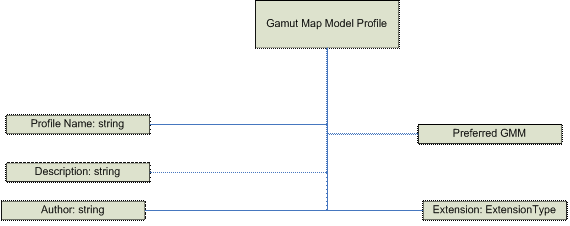
Architecture de profil de modèle de carte gamut

L’échantillonnage de l’espace colorant du dispositif de sortie est effectué en itérant dans les colorants de 0.0 à 1.0 avec une étape fractionnaire, en accumulant toutes les combinaisons de chaque colorant à chaque étape, puis en les convertissant de l’espace colorant du périphérique en espace d’apparence de couleur à l’aide de la méthode DM::D eviceToColorimetricColors suivie de la méthode CAM::ColorimetricToAppearanceColors. Voici un exemple de la façon dont cette opération est effectuée pour RVB.

For (red= 0.0; red <= 1.0; red += redStep) {

     For (green = 0.0; green <= 1.0; green += greenStep) {

          For (blue = 0.0; blue <= 1.0; blue += blueStep) {

               Colorants[0] = red; colorants[1] = green; colorants[2] = blue;

               pRGBDM->DeviceToColorimetricColors(1, colorants, &amp;XYZ);

               pCAM->ColorimetricToAppearanceColors(1, &amp;XYZ, &amp;JCh);

          }

     }

}

Génération de la limite de gamut

Il existe trois composants à la limite de la gamme : les primaires, les échantillons neutres et les interpréteurs de commandes. Les primaires sont générées en prenant les primaires d’appareil et en appliquant la transformation DeviceToColorimetric/ColorimetricToAppearance. Les échantillons neutres sont générés en échantillonnant l’espace colorant de l’appareil dans la zone neutre et en appliquant la même transformation. Pour trois dispositifs colorants (RVB ou CMY), les échantillons neutres sont définis comme ayant tous les colorants égaux, par exemple, R == G == B. Pour CMJN, les échantillons neutres sont définis comme ayant C == M == Y == 0.

Les facteurs qui influencent les données utilisées pour créer la limite de la gamme sont les exemples de données (appareils de base uniquement) et les conditions d’affichage. La taille d’étape utilisée pour effectuer l’échantillonnage complet de l’espace colorant (pour les moniteurs et pour la coque plausible) est une constante interne et n’est pas disponible pour une manipulation extérieure. La modification des conditions d’affichage modifie le comportement du modèle d’apparence de couleur (CAM) et modifie la forme de la limite de gamut. Vous devez donc générer une limite de gamut liée au profil des conditions d’affichage. Si des exemples de données sont utilisés, comme dans le cas des imprimantes de base et des périphériques de capture, les exemples auront un impact important sur la forme de la gamme de référence et affecteront le comportement du modèle lui-même.

Pour les périphériques d’entrée, tels que les caméras et les scanneurs, différents échantillonnages sont utilisés pour générer l’interpréteur de commandes de référence et l’interpréteur de commandes plausible. L’interpréteur de commandes de référence est généré à partir des mesures utilisées pour initialiser le modèle d’appareil. L’interpréteur de commandes plausible est généré de la même façon que l’illustration précédente pour les périphériques de sortie. La différence est que lorsque vous entrez une cible classique, vous n’obtenez pas de valeurs complètement saturées (où R, G ou B = 255). Vous devez extrapoler à l’aide du modèle d’appareil pour estimer ces valeurs.

Schéma GMMP

<?xml version="1.0" encoding="UTF-8"?>
<xs:schema 
  xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
  xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
  targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
  xmlns:xs="http://www.w3.org/2001/XMLSchema"
  elementFormDefault="qualified"
  attributeFormDefault="unqualified"
  blockDefault="#all"
  version="1.0">

  <xs:annotation>
    <xs:documentation>
      Gamut Map Model profile schema.
      Copyright (C) Microsoft. All rights reserved.
    </xs:documentation>
  </xs:annotation>

  <xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />

  <xs:element name="GamutMapModel">
    <xs:complexType>
      <xs:sequence>
        <xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
        <xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="DefaultBaselineGamutMapModel">
          <xs:simpleType>
            <xs:restriction base="xs:string">
              <xs:enumeration value="HPMinCD_Absolute"/>
              <xs:enumeration value="HPMinCD_Relative"/>
              <xs:enumeration value="SGCK"/>
              <xs:enumeration value="HueMap"/>
            </xs:restriction>
          </xs:simpleType>
        </xs:element>
        <xs:element name="PlugInGamutMapModel" minOccurs="0">
          <xs:complexType>
            <xs:sequence>
              <xs:any namespace="##other" processContents="skip"
                minOccurs="0" maxOccurs="unbounded" />
            </xs:sequence>
            <xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
          </xs:complexType>
        </xs:element>
      </xs:sequence>
      <xs:attribute name="ID" type="xs:string" use="optional" />
    </xs:complexType>
  </xs:element>
</xs:schema>

Éléments de schéma GMMP

GamutMapModel

Cet élément est une séquence des sous-éléments suivants :

1. Chaîne ProfileName,
2. DefaultBaselineGamutMapModel,
3. Chaîne de description facultative,
4. Chaîne d’auteur facultative,
5. PlugInGamutMap facultatif et
6. ExtensionType facultatif.

Conditions de validation : chaque sous-élément est validé par son propre type.

Espace de noms

xmlns:gmm= »http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"

targetNamespace= »http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"

Version

Version « 1.0 » avec la première version de Windows Vista.

Conditions de validation : 1.0 dans Windows Vista. Les versions <2.0 sont également valides pour prendre en charge les modifications de format sans rupture.

Documentation

Schéma de profil de modèle de carte de gamut.

Copyright (C) Microsoft. Tous droits réservés.

Conditions de validation : chaque sous-élément est validé par son propre type.

Type DefaultBaselineGamutMapModel

Type UINT

Valeurs d’énumération :

« MinCD\_Absolute » « MinCD\_Relative » « SIG\_KNEE » « HueMap »

Conditions de validation : les valeurs doivent correspondre à l’une des énumérations ci-dessus.

PlugInGamutMapType

Cet élément est une séquence d’un GUID GUIDType et de tous les sous-éléments.

Conditions de validation : le GUID est utilisé pour correspondre au GUID de la DLL PlugIn GMM. Il existe un maximum de 100 000 sous-éléments personnalisés.

ExtensionType

Cet élément est une séquence facultative de tous les sous-éléments.

Conditions de validation : il peut y avoir un maximum de 100 000 sous-éléments.

Algorithmes de base GMMP

Alignement des axes neutres

La plupart des algorithmes de mappage de gamut ont pour objectif de mapper l’axe neutre de l’appareil source à l’axe neutre de l’appareil de destination : autrement dit, le blanc passe au blanc, le noir au noir et le gris au gris. Cela est résolu en partie par la mise à l’échelle de la luminosité des couleurs sources pour qu’elle corresponde à la plage de luminosité de l’appareil de destination. Mais cela ne répond pas complètement au problème.

Il est une propriété physique de la plupart des appareils d’imagerie que la chromaticité du blanc de l’appareil ne correspond pas exactement à la chromaticité de l’appareil noir. Par exemple, le blanc du moniteur dépend de la somme des chromaticités et des luminosités relatives des trois primaires, tandis que le moniteur noir dépend de la réflectance de la surface d’affichage. Le blanc de l’imprimante dépend de la chromaticité du papier, tandis que le noir de l’imprimante dépend de l’encre ou du toner utilisé. Un modèle d’apparence qui mappe le blanc de l’appareil exactement à l’axe neutre de l’espace d’apparence (chroma exactement égal à zéro) ne mappe pas l’appareil en noir à l’axe neutre. Étant donné que l’œil est plus sensible aux différences chromatiques à mesure que la légèreté augmente, le gris moyen sera représenté comme encore plus chromatique que le noir d’appareil. (La figure 1 illustre la courbure des axes neutres en deux dimensions. En fait, les axes neutres forment une courbe plus complexe en trois dimensions.)

Alors que le CAM prédit que ces couleurs neutres d’appareil apparaîtront chromatiques, les observateurs réels semblent compenser cela. La plupart des gens ne considèrent pas ces valeurs neutres d’appareil comme chromatiques. Pour la plupart des modèles de mappage de gamut, par conséquent, vous devez continuer à mapper des sources neutres à des appareils neutres.

Pour mapper des sources neutres à des appareils neutres, ajustez les limites de la gamme source et de destination et chaque pixel lorsque vous appliquez l’algorithme de mappage de gamut. Commencez par ajuster chaque valeur dans la couleur source afin que l’axe neutre de l’appareil source au niveau de la luminosité de la couleur source tombe directement sur l’axe neutre de l’espace d’apparence. (Voir le côté gauche de la figure 1.) Ajustez ensuite la description de la limite de gamut de l’appareil de destination afin que chaque couleur de l’axe neutre de l’appareil de destination au niveau de la couleur de la limite de la gamme de l’appareil de destination tombe directement sur l’axe neutre de l’espace d’apparence. (Voir le côté droit de la figure 1.)

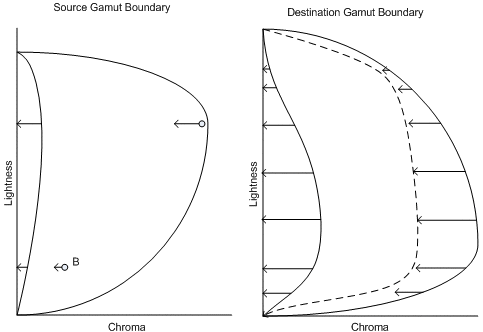
Figure 1 : Alignement des axes neutres illustrés. Gauche : ajustement des points sources par rapport à l’axe neutre de l’appareil source. Droite : ajustement de la description de la limite de gamut de destination par rapport à la description de la limite de la gamme de destination.

Notez que vous ajustez chaque valeur de pixel source par rapport à l’axe neutre à cette valeur de luminosité. Cela garantit que les appareils sources neutres tomberont sur l’axe neutre du modèle d’apparence. Vous déplacez également toutes les autres couleurs à cette légèreté du même montant, de sorte qu’il n’y ait pas de discontinuités dans la représentation de la gamme source. Vous devez décaler par des quantités différentes à différents niveaux de luminosité, car les neutres de l’appareil source ne sont pas représentés comme également chromatiques aux différents niveaux de luminosité. De toute évidence, il ne s’agit pas d’une transformation triviale.

La gestion des valeurs de l’appareil de destination est un peu plus difficile. Au départ, vous ajustez la limite de la gamme de destination entière de la même manière, mais par rapport à l’axe neutre de l’appareil de destination. Ceci est illustré dans la figure 1 sur le côté droit. Cet ajustement garantit que les valeurs grises sources seront mappées aux valeurs grises de destination. Il s’agit de l’espace dans lequel les algorithmes de mappage de gamut fonctionnent.

Toutefois, cet espace ne décrit pas avec précision le véritable comportement de l’appareil de destination. Vous devez inverser le mappage avant que les couleurs mappées par gamut soient transmises au modèle d’apparence et au modèle d’appareil de destination. Vous décalerez toutes les valeurs mappées par l’opposé du décalage appliqué précédemment à l’axe neutre de l’appareil de destination. Cela mappe l’axe neutre de destination à la valeur représentée à l’origine par le CAM. Il en est de même pour la limite de la gamme et toutes les valeurs intermédiaires.

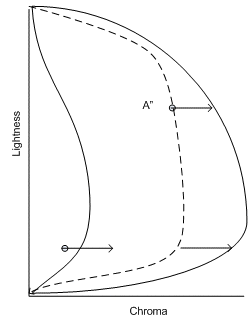
Figure 2 : Annulation de l’alignement de l’axe neutre de l’appareil de destination

Différence de couleur minimale (MinCD)

Minimum Color Difference (MinCD) Relative et Absolute versions : équivalent à l’intention colorimétrique ICC.

Notes

Le GMM MinCD convient pour le mappage de graphiques et de dessins en courbes contenant des couleurs de « logo » (couleurs spot), des dégradés de couleurs de logo avec des couleurs hors gamme et pour la phase finale des transformations de vérification. Bien que le GMM MinCD puisse être utilisé pour les images photographiques qui se trouvent entièrement dans la gamme de destination, il n’est pas recommandé pour le rendu général des images photographiques. Le mappage des couleurs hors gamut aux couleurs de la surface de gamut de destination peut entraîner des artefacts indésirables, tels que des irrégularités de ton ou de chroma dans des dégradés lisses qui franchissent la limite de gamut. BasicPhoto est recommandé pour les images photographiques. Si une image photographique ou contone nécessite un mappage de gamut autre que BasicPhoto, l’alternative doit consister à créer un module GMM plug-in implémentant ce mappage, au lieu d’utiliser MinCD.

 

Les couleurs de la gamme restent inchangées. Pour les couleurs hors gamut, la luminosité et la couleur sont ajustées en recherchant le point dans la gamme de destination qui a la distance de couleur minimale par rapport aux points d’entrée hors gamut. La distance de couleur est calculée dans l’espace JCh. Toutefois, vous pondez différemment la distance en légèreté (J) et la distance en chroma (C) ou en teinte (h). Une fonction de poids dépendant de la chromaie est utilisée pour la distance en légèreté, de sorte que le poids est plus petit pour la petite chromatique et plus grand pour la grande chroma jusqu’à ce qu’un seuil chromatique soit atteint, après quoi le poids reste à 1, c’est-à-dire le même poids que la distance dans la chroma ou la teinte. Cela suit l’utilisation recommandée pour CMC et CIEDE2000. Il existe deux variantes : colorimétrique relative et colorimétrique absolue.

Colorimétrique relative : Tout d’abord, alignez les axes neutres source et de destination, comme décrit précédemment. Ensuite, attachez la couleur de source ajustée à la limite de la gamme de destination ajustée. (Voir la figure 4. Mappage chromatique le long d’une légèreté constante.) Réajustez les valeurs de l’appareil de destination comme décrit précédemment. Dans le cas d’une limite de gamme de destination monochrome, le découpage chromatique signifie que la valeur chromatique (C) est définie sur zéro (0,0).

Colorimétrique absolue : Cela est similaire à la colorimétrie relative, mais sans l’alignement de l’axe source et de destination neutre. La valeur source est directement coupée sur l’axe neutre de destination. Notez que si les limites de la gamme source et de destination sont monochromes, le comportement est identique à la variante colorimétrique relative ; autrement dit, l’alignement des axes neutres est effectué, puis la chroma est coupée à zéro. Cela garantit qu’une sortie raisonnable est atteinte même si les milieux et les colorants sont sensiblement différents.

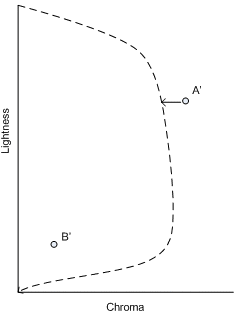
Figure 3 : Découpage minCD sur la gamme ajustée

BasicPhoto

Vue d’ensemble

BasicPhoto : équivalent à l’intention préférée, picturale ou perceptive de la CPI.

Cet algorithme est une variante du mappage de la luminosité sigmoidale et de la mise à l’échelle du genou du cusp (CUSP) qui sont décrits par CIE TC8-03 dans CIE156:2004. Cet algorithme de variante prend en charge les descripteurs de limites de gamut (GBD) avec des interpréteurs de commandes à deux gamuts ; c’est-à-dire des GBD avec un interpréteur de commandes de référence et un interpréteur de commandes plausible. L’algorithme SGCK, qui suppose à l’origine qu’un seul interpréteur de données gamut dans le GBD, est basé sur l’algorithme de SIG_KNEE (Braun, 1999), qui intègre le mappage de légèreté sigmoïdale et la mise à l’échelle de la fonction genoux proposées par Braun et Fairchild (1999), combiné avec la dépendance chromatique de GCUSP (Morovic, 1998). Il maintient la constante de teinte perçue, par exemple, l’angle de teinte dans jab corrigé de teinte, et utilise une échelle de légèreté sigmoïdale générique (indépendante de l’image) qui est appliquée de manière dépendante de la chromaie et d’une fonction de genou à 90 pour cent. La variante est mise à l’échelle le long de lignes de légèreté constante.

Cas de l’interpréteur de commandes à gamut unique

Il est utile de passer en revue l’algorithme dans le cas où les GBD source et de destination n’ont qu’un seul interpréteur de commandes gamut. Dans ce cas, l’algorithme se compose des calculs suivants.

Tout d’abord, effectuez un mappage de légèreté initiale à l’aide de la formule suivante :

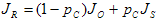(1)

où Jₒ est la légèreté d’origine et J_R est la légèreté de reproduction.

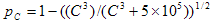(2)

Lorsque la limite de la gamme source est monochrome, la valeur chromatique est égale à zéro pour la limite monochrome en raison de l’alignement neutre de l’axe. Cela entraîne le cas dégénéré où C est égal à zéro. Dans ce cas, p_C est défini sur 1.

p_C est un facteur de pondération chroma-dépendant (Morovic, 1998) qui dépend de la chroma de la couleur d’origine, C et _JS sont le résultat de la légèreté d’origine mappée à l’aide d’une fonction sigmoïdale.

 

Pour calculer _JS (Braun et Fairchild, 1999), une table de recherche unidimensionnelle (LUT) entre les valeurs de légèreté d’origine et de reproduction est d’abord configurée sur la base d’une fonction normale cumulative discrète (S).

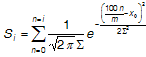(3)

où x ₀ et S sont respectivement la moyenne et l’écart-type de la distribution normale et i = 0,1,2... m,m est le nombre de points utilisés dans le LUT. S_i est la valeur de la fonction normale cumulative pour i /m pour cent. Les paramètres dépendent de la légèreté du point noir de la gamme de reproduction et peuvent être interpolés à partir du tableau 1. Pour plus d’informations sur le calcul de ces paramètres, voir Braun et Fairchild (1999, p. 391).

J _minOut

5,0

10.0

15.0

20,0

x ₀

53.7

56.8

58.2

60.6

S

43,0

40,0

35,0

34,5

Tableau 1 : Calcul du paramètre de compression de légèreté BasicPhoto

Pour utiliser S comme LUT (S _LUT ) de mappage de luminosité, il doit d’abord être normalisé dans la plage de luminosité de [0,100]. Les données normalisées sont ensuite mises à l’échelle dans la plage dynamique de l’appareil de destination, comme indiqué dans l’équation 4, où J_{min\ Out} et J_{max\ Out} sont les valeurs de légèreté du point noir et du point blanc du support de reproduction, respectivement.

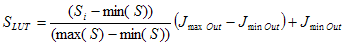(4)

À ce stade, les valeurs JS peuvent être obtenues à partir du _LUT S en interpolant entre les points m des valeurs J O' et J S correspondantes qu’il contient, et en utilisant l’équation suivante comme entrée.

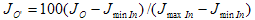(5)

J _minIn est la valeur de légèreté du point noir du support d’origine, J _maxIn est la valeur de légèreté du point blanc du support d’origine et J _O est la légèreté d’origine. Pour référence ultérieure, vous pouvez désigner par S la fonction sigmoïdale définie de la manière qui vient d’être décrite, comme illustré dans la figure 4 suivante.

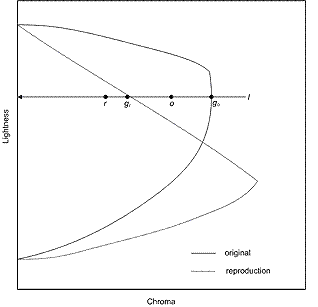
Figure 4 : Mappage chromatique le long d’une luminosité constante

Deuxièmement, si la limite de gamut de destination est chromatique, compressez la chroma le long des lignes de légèreté constante (l) et effectuez la compression comme suit.

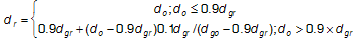(6)

où d représente la distance par rapport à E sur l; g représente la limite de la gamme moyenne ; r représente la reproduction ; et o la figure 5 d’origine.

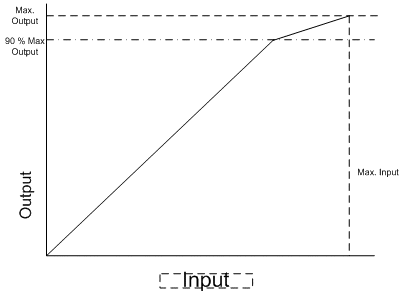
Figure 5 : Compression chromatique et légèreté dans BasicPhoto

Si la limite de gamut de destination est monochrome, la valeur de chroma est rogné sur zéro.

Troisièmement, utilisez un clip MinCD (décrit précédemment) pour éliminer toute erreur résiduelle.

Amélioration du noir

L’algorithme précédent peut être modifié pour améliorer le noir lorsque la destination est un périphérique d’imprimante. Le problème est lié au choix de J_minOut, qui ne correspond généralement pas à la couleur la plus foncée qu’une imprimante peut produire.

Plus précisément, la couleur avec la densité la plus élevée, obtenue en plaçant 100 % d’encres (ou la couverture maximale possible, si la limitation gcr/encre est appliquée), n’est généralement pas « neutre » dans l’espace d’apparence des couleurs. Voir la figure 6. En d’autres termes, si la légèreté minimale neutre est utilisée pour l’appareil de destination, le scaler de luminosité construit correspond à une légèreté minimale qui n’est pas la densité la plus élevée que peut atteindre l’imprimante. Considérez le cas d’usage ultérieur du moniteur à l’imprimante. Le moniteur noir, R=G=B=0, sera alors imprimé comme n’étant pas la densité la plus élevée. L’impact sur la qualité de l’image est qu’il y a un manque de profondeur et de contraste.

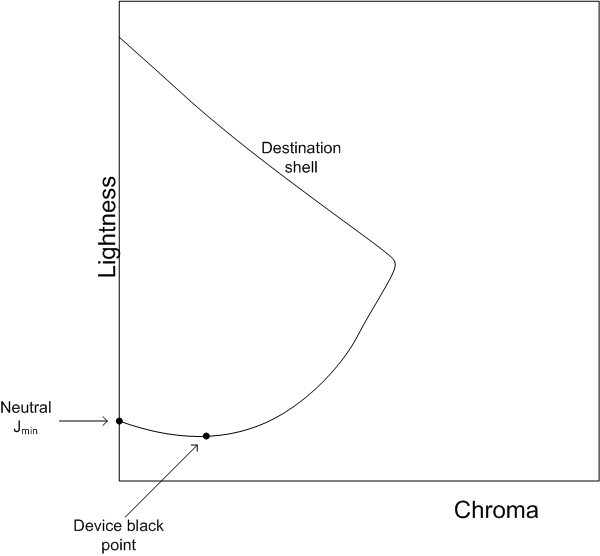
Figure 6 : Le point noir de l’appareil peut être plus foncé que la luminosité minimale neutre.

Supposons que la destination « point noir de l’appareil » est Jkakbk/JkCkh k. Si C k n’est pas zéro, le point noir de l’appareil n’est pas neutre par rapport à CAM02. Si vous utilisez J k pour la destination « légèreté minimale neutre » dans la construction du scaler de légèreté ; c’est-à-dire, définition

J_minOut = Jk

et l’appliquez à l’interpréteur de commandes de gamut source, vous obtenez la configuration illustrée dans la figure 7. Dans la figure, le plan de teinte correspond à h k.

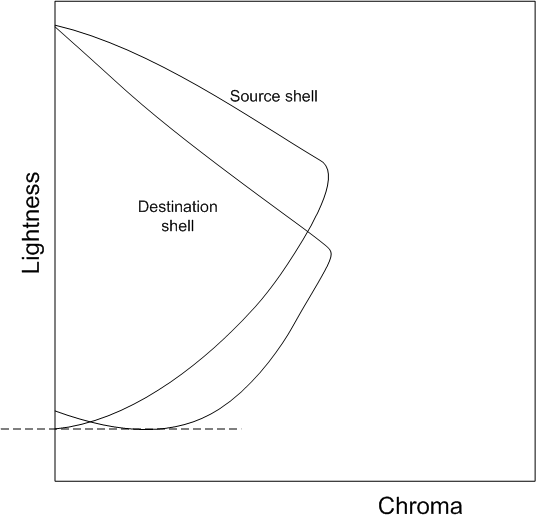
Figure 7 : Géométrie à l’aide du scaler de luminosité modifié avec point noir de l’appareil de destination

Pour permettre à l’algorithme de compression de chroma suivant de continuer, vous souhaitez aligner les luminosités maximale et minimale sur les interpréteurs de commandes source et de destination. Pour ce faire, vous pouvez ajuster l’interpréteur de commandes de destination entre J _neutralMin et J k en déplaçant les points vers la gauche. De plus, cette transformation doit être appliquée sur l’ensemble de l’espace Jab, et pas seulement sur le plan de teinte correspondant à h k.

La transformation est

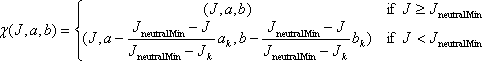
La figure 8 montre l’effet de la transformation.

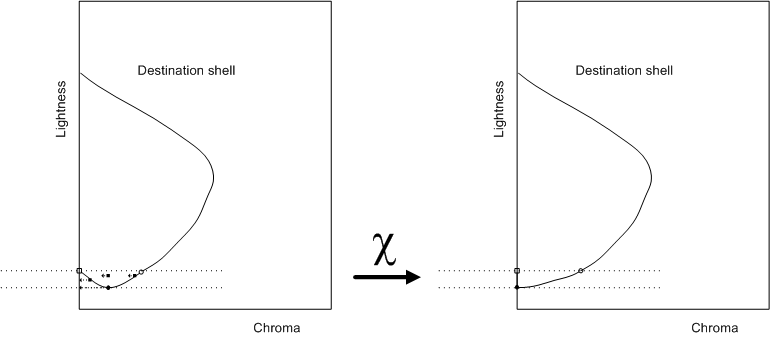
Figure 8 : Géométrie à l’aide du scaler de luminosité modifié avec point noir de l’appareil de destination

Après avoir appliqué l’algorithme de compression chromatique habituel, le point doit être « déplacé en arrière », c’est-à-dire que la transformation inverse doit être appliquée pour obtenir la couleur mappée finale.

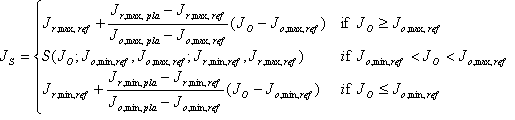
Le cas des interpréteurs de commandes à double gamut

L’objectif est de généraliser SIG_KNEE pour l’interpréteur de commandes à gamut unique au cas où le GBD de l’appareil source ou le GBD de l’appareil de destination a une structure à deux interpréteurs de commandes. L’interpréteur de commandes interne sera appelé l’interpréteur de commandes de référence, tandis que l’interpréteur de commandes externe sera appelé l’interpréteur de commandes plausible. Vous souhaitez prendre en compte les cas suivants.

(a) Le GBD source et le GBD de destination ont une structure à deux interpréteurs de commandes.

(b) Le GBD source a une structure à deux interpréteurs de commandes ; le GBD de destination n’a qu’un seul interpréteur de commandes.

(c) Le GBD source n’a qu’un seul interpréteur de commandes ; le GBD de destination a une structure à deux interpréteurs de commandes.

(d) Le GBD source et le GBD de destination n’ont qu’un seul interpréteur de commandes.

Le cas (d) est le cas de l’interpréteur de commandes à gamut unique qui a été abordé précédemment. Pour les cas (a), (b) et (c), vous pouvez généraliser la mise à l’échelle de légèreté pour utiliser les informations supplémentaires de la structure du double interpréteur de commandes. Dans les cas (b) et (c) où la source ou la destination n’a qu’un seul interpréteur de commandes, vous introduisez un « interpréteur de commandes de référence induit » qui sera abordé dans une section suivante, « Interpréteur de commandes de référence induit ». L’algorithme général pour deux interpréteurs de commandes sera décrit pour le cas (a). Une fois la construction de l’interpréteur de commandes de référence induit expliquée, l’algorithme peut également être appliqué aux cas (b) et (c). Comme pour la compression chromatique, le taux de compression est déterminé par les plus grandes coques disponibles. En d’autres termes, si l’interpréteur de commandes plausible et l’interpréteur de commandes de référence sont disponibles, l’interpréteur de commandes plausible sera utilisé ; sinon, l’interpréteur de commandes de référence sera utilisé.

Mise à l’échelle de la légèreté généralisée

L’existence de deux interpréteurs de commandes pour le GBD source et le GBD de destination signifie que vous devez mapper un ensemble de quatre points du GBD source à un ensemble correspondant dans le GBD de destination.

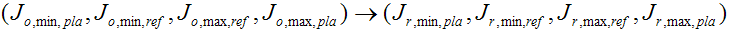
Les indices ont les significations suivantes.

o ou r : « original » (source) ou « reproduction » (destination)

min ou max : luminosité neutre minimale ou luminosité neutre maximale

pla ou ref : Interpréteur de commandes plausible ou interpréteur de commandes de référence

L’ordre de chaque quadruplé est également l’ampleur relative attendue de ces points.

La carte Lightness Rescaling utilise les mêmes deux premières équations que l’interpréteur de commandes unique, mais JS est défini de manière fragmenté comme suit.

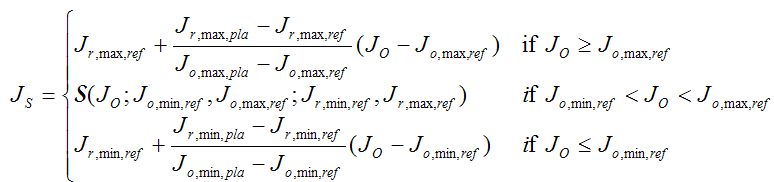(7)

En d’autres termes, il est sigmoïdal dans l’interpréteur de commandes de référence et linéaire à l’extérieur. Voir figure 9.

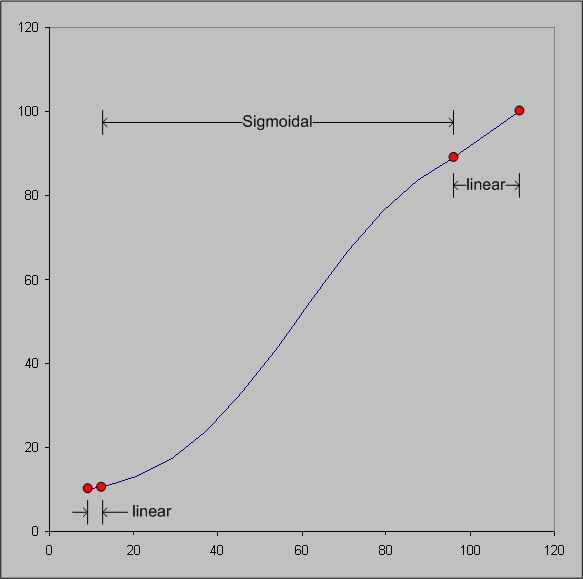
Figure 9 : Fonction de mise à l’échelle de la légèreté pour les GBD à deux shells

INTERPRÉTEUR DE COMMANDES DE RÉFÉRENCE INDUIT

Si un GBD a un interpréteur de commandes et l’autre GBD a deux interpréteurs de commandes, vous devez créer un « interpréteur de commandes de référence » pour le GBD avec un seul interpréteur de commandes. L’interpréteur de commandes existant, qui serait appelé Interpréteur de commandes de référence, sera remplacé par « Interpréteur de commandes plausible ». En fait, vous n’avez pas besoin de créer un interpréteur de commandes dans l’espace Jab complet. Étant donné que la mise à l’échelle légère utilise uniquement J max et J min, vous n’avez qu’à créer ces valeurs pour l’interpréteur de commandes de référence induit. Il existe deux cas, selon le GBD qui a deux interpréteurs de commandes.

Cas 1 : Le GBD source a deux interpréteurs de commandes ; le GBD de destination a un interpréteur de commandes.

Déterminer l’interpréteur de commandes de référence induit par la destination sur l’axe neutre ; c’est-à-dire les références J _{r,\ min,\ ref} et J _{r,\ max,\ de} l’interpréteur de commandes. Pour ce faire, utilisez l’algorithme suivant.

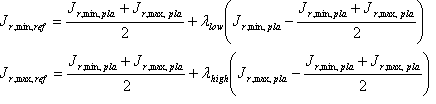
Les facteurs ? _bas et ? _{les hauts} contrôlent la séparation entre l’interpréteur de commandes plausible et l’interpréteur de commandes de référence. La valeur 1 signifie que les valeurs J _min ou J mₐₓ valeurs coïncident. Leurs valeurs sont « induites » à partir de l’interpréteur de commandes de référence source et de l’interpréteur de commandes plausible source.

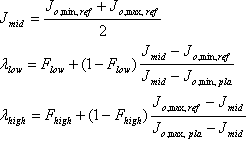
Les « facteurs fudge » F _low et F _high sont des paramètres paramétrables qui doivent se situer entre 0 et 1. Si la valeur est 0, les J _min ou J mₐₓ sont directement induits à partir des interpréteurs de commandes source. Dans ce cas, choisissez F _faible = 0,95 et F _élevé = 0,1.

Cas 2 : Le GBD source a un interpréteur de commandes ; le GBD de destination a deux interpréteurs de commandes.

Déterminer l’interpréteur de commandes de référence induit par la source sur l’axe neutre ; _{c’est-à-dire les valeurs J o,\ min,\ ref} et J _{o,\ max,\ de} l’interpréteur de commandes. Pour ce faire, utilisez l’algorithme suivant.

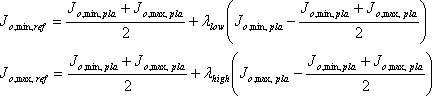
Là encore, les facteurs ? _bas et ? _high contrôle la séparation entre l’interpréteur de commandes plausible et l’interpréteur de commandes de référence. La valeur 1 signifie que les valeurs J _min ou J mₐₓ coïncident. Leurs valeurs sont « induites » à partir de l’interpréteur de commandes de référence source et de l’interpréteur de commandes plausible source :

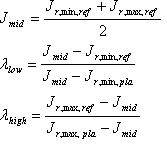
Raisons des modifications apportées aux recommandations du CIE TC8-03

BasicPhoto diffère des recommandations CIE TC8-03 des manières suivantes.

1. La chroma n’est pas compressée vers le cusp, mais sur des lignes de légèreté constante.
2. La plage de luminosité utilise la légèreté de la couleur la plus foncée de la gamme plutôt que le point auquel la limite de gamut traverse l’axe neutre.
3. BasicPhoto prend en charge à la fois un interpréteur de commandes de gamut de référence et un interpréteur de commandes de gamut plausible, si l’une ou l’autre limite de gamut dans la transformation a deux interpréteurs de commandes.
4. BasicPhoto utilise CIECAM02 ; au lieu d’utiliser CIECAM97s pour convertir en D65 à 400 cd/m2, puis d’utiliser l’espace de couleur IPT RIT.

La première modification a été apportée pour éviter les problèmes d’inversion de tonalité qui peuvent se produire lors de l’utilisation de la compression vers un cusp. Comme le montre la figure 10, la compression du cusp peut provoquer des inversions de tonalité. Cela peut se produire lorsque les couleurs de haute couleur sont plus claires que les couleurs de couleur inférieure. Étant donné que SGCK compresse chaque pixel indépendamment en légèreté et en couleur, il n’est pas garanti de conserver la relation de légèreté entre les valeurs de pixels après la compression. L’inconvénient bien connu de cette décision de compresser sur des lignes de légèreté constante est que vous pouvez subir des pertes de chroma, en particulier dans les zones où la limite de gamut de destination est très plate, comme c’est le cas avec les jaunes brillants.

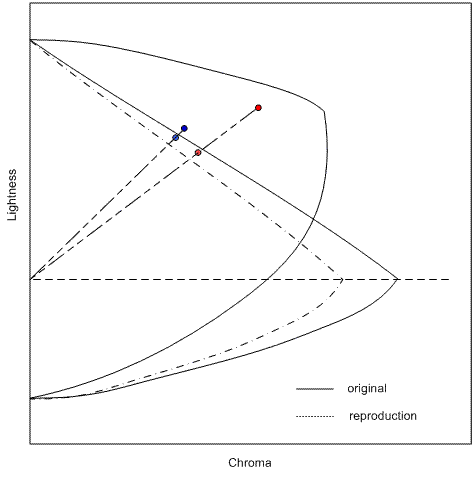
Figure 10 : Inversion de tonalité provoquée par SGCK

Figure 11 : image d’origine, résultat SGCK et résultat BasicPhoto

La figure 11 illustre cette inversion de tonalité. À gauche se trouve une image originale capturée par un appareil photo numérique ; au centre, l’image telle que reproduite par SGCK ; et à droite, l’image telle que reproduite par BasicPhoto. L’image à gauche se trouve dans l’espace de couleurs de l’appareil photo numérique, les images centre et droite se trouvent dans l’espace de couleurs d’un écran vidéo LCD. Dans l’image d’origine, la partie supérieure de la théière est plus foncée que le bas, car le bas reflète la nappe sur laquelle elle est assise. Dans l’image SGCK, la partie supérieure est en fait plus légère que la partie inférieure, en raison de l’inversion de tonalité. En outre, il est difficile de voir les articles reflétés dans la partie inférieure de la théière. À droite, BasicPhoto a fixé l’inversion de ton et les articles réfléchis sont plus clairement reconnaissables.

La deuxième modification a été apportée pour améliorer la reproduction des couleurs presque noires sur les imprimantes où le noir le plus noir ne tombe pas directement sur l’axe neutre CIECAM02. La figure 12 suivante montre une image convertie en sRGB ; reproduit pour une imprimante jet d’encre RVB à l’aide de SGCK ; et reproduit pour la même imprimante à l’aide de BasicPhoto. L’image au centre n’utilise pas le noir complet de l’appareil, et elle n’a donc pas le contraste observé dans l’original. Le contraste est restauré avec BasicPhoto.

Figure 12 : Noir amélioré

La troisième modification a été apportée pour améliorer la reproduction des couleurs pour les appareils photo numériques. En particulier dans les cas où l’appareil photo numérique a été profilé à l’aide d’une cible de référence, une description de limite de gamut créée à partir de couleurs mesurées peut ne pas inclure toutes les couleurs qui peuvent être capturées dans une scène du monde réel. Au lieu de couper toutes les couleurs sur la gamut de la cible de couleur mesurée, vous autorisez l’extrapolation à produire une limite de gamut plausible. L’algorithme BasicPhoto est conçu pour prendre en charge une telle limite de gamuts extrapolée.

La quatrième modification a été apportée, car CIECAM02 fonctionne bien pour le mappage de gamuts. Le processus recommandé par TC8-03 pour convertir les couleurs des appareils en D65 à 400 cd/m2, puis utiliser l’espace de couleurs RIT IPT est à la fois gourmand en calculs et chronophage.

Mappage Hue

HueMap est l’équivalent de l’intention de saturation ICC.

Si la limite de gamut source ou la limite de gamut de destination ne contient pas de valeurs primaires, ce modèle revient au modèle MinCD (relatif) décrit dans une section précédente ; par exemple, les appareils pour lesquels les primaires ne peuvent pas être déterminées (profils ICC avec plus de quatre canaux) ou les profils ICC monochromes.

Cet algorithme ajuste d’abord la teinte de la valeur de couleur d’entrée. Ensuite, il ajuste simultanément la légèreté et la chromaité, à l’aide d’un mappage de cisaillement. Enfin, il clipse la valeur de couleur pour s’assurer qu’elle se trouve dans gamut.

La première étape consiste à déterminer les « roues Hue ». Recherchez les valeurs JCh pour les couleurs primaires et secondaires pour l’appareil source et l’appareil de destination. Vous n’envisagez que les composants hue. Il en résulte une roue de teinte primaire ou secondaire avec six points de couleur pour chaque appareil. (Voir la figure 13.)

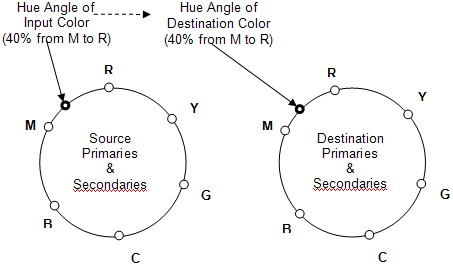
Figure 13 : Roues Hue

De meilleurs résultats peuvent être obtenus si le principal bleu source n’est pas pivoté vers le principal bleu de destination. Au lieu de cela, l’angle de teinte primaire bleu source est utilisé comme angle de teinte primaire bleu de destination.

Ensuite, effectuez les rotations de teinte pour chaque couleur d’entrée à partir de l’image source,

a)À l’aide de l’angle de teinte de la couleur d’entrée, déterminez l’emplacement de la couleur sur la roue de teinte source par rapport aux deux couleurs primaires ou secondaires adjacentes. L’emplacement peut être considéré comme un pourcentage de la distance entre les primaires. Par exemple, la teinte de couleur d’entrée est de 40 % du chemin entre la valeur de teinte de Magenta et la valeur de teinte rouge.

b)Sur la roue de teinte de destination, recherchez l’angle de teinte associé, par exemple, de 40 % de Magenta à Rouge. Cette valeur sera l’angle de teinte de destination.

En général, les primaires sources et les secondaires ne seront pas aux mêmes angles de teinte que les primaires et les secondaires de destination; autrement dit, l’angle de teinte de destination sera généralement différent de l’angle de teinte source.

Par exemple, supposons que les roues hue produisent les valeurs suivantes :

Source M = 295 degrés, Source R = 355 degrés.

Destination M = 290 degrés, Destination R = 346 degrés.

Si l’angle de teinte de la couleur d’entrée est de 319 degrés, il correspond à 40 % de l’angle (24 degrés) de la source M à la source R. L’angle de M à R est de 60 degrés et l’angle de M à la teinte d’entrée est de 24 degrés. Calculez l’angle de la destination qui est de 40 % de la destination M à la destination R (22 degrés), de sorte que l’angle de teinte de la couleur de destination est de 312 degrés.

Ensuite, calculez les points de référence hue pour la teinte source et la teinte de destination. Pour calculer le point de référence de teinte pour une valeur h (hue) particulière, vous souhaitez rechercher la valeur J (légèreté) et la valeur C (chroma).

• Recherchez la valeur J du point de référence de teinte en interpolant entre les valeurs J des points primaires ou secondaires adjacents, à l’aide de la position relative de la teinte ; par exemple, 40 % dans cet exemple.
• Recherchez la valeur C maximale à cette valeur J et h. Vous avez maintenant le JCh du point de référence hue pour cette teinte.

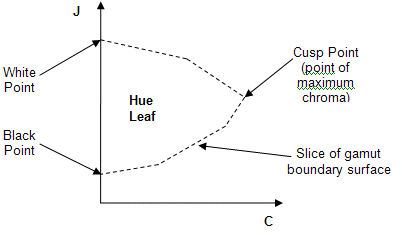
Figure 14 : Feuille de teinte (visualisation d’une tranche de limite de gamut à une teinte spécifique)

L’étape suivante consiste à calculer le mappage de cisaillement pour chaque pixel. Tout d’abord, visualisez une feuille de teinte à partir du gamut source pour l’angle de teinte de la couleur source et une feuille de teinte du gamut de destination pour l’angle de teinte de destination calculé pendant la rotation de teinte. Les feuilles de teinte sont créées en prenant une « tranche » à partir de la surface limite du gamut JCh à un angle de teinte spécifique (voir figure 14).

REMARQUE : Pour des raisons d’optimisation des performances, les feuilles hue ne sont pas réellement créées ; ils sont décrits et affichés ici à des fins de visualisation uniquement. Les opérations sont effectuées directement sur la surface de limite de gamut à la teinte spécifiée. Vous calculez ensuite les points de référence hue pour déterminer le mappage de cisaillement.

• Effectuez une mise à l’échelle légère pour mapper les points noir et blanc de la feuille source à la feuille de destination (voir figure 15). Les points noir et blanc de la feuille de teinte source sont mappés linéairement aux points noir et blanc de la feuille de teinte de destination, en mettant à l’échelle toutes les coordonnées J de la limite source. La valeur de couleur d’entrée mappée est mise à l’échelle de la même manière.

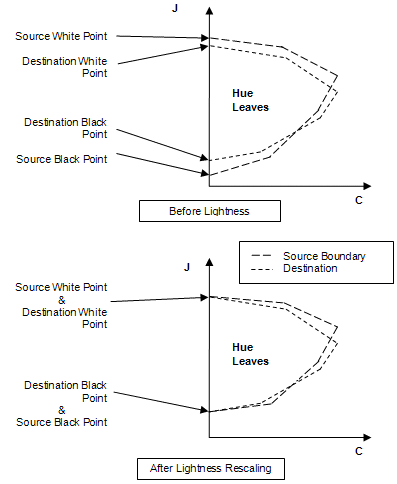
Figure 15 : Mappage de luminosité

• Déterminez les points de référence de teinte pour chaque feuille de teinte. Appliquez un mappage de cisaillement à la feuille source afin que les points de référence source et de destination coïncident (voir la figure 16). Le point de référence d’un gamut à une teinte spécifique est le point de référence de teinte interpolé entre les primaires adjacentes. Le point de référence de la feuille de teinte source est mappé linéairement au point de référence de la feuille de teinte de destination, à l’aide d’une opération de cisaillement qui verrouille l’axe J, en gardant les points noirs et les points blancs à l’arrêt. Les points noirs, les points blancs et les points de référence des feuilles de teinte source et de destination doivent coïncider.
• Appliquez le mappage de cisaillement à la valeur de couleur d’entrée ajustée en légèreté. Les coordonnées J et C de la valeur de couleur source sont mises à l’échelle proportionnellement, par rapport à sa distance par rapport à l’axe J.
• Ensuite, une compression subtile de la légèreté chromao-dépendante vers la valeur J du point de référence de teinte est effectuée sur le point de couleur mappé de cisaillement. La compression vers la référence de teinte J est effectuée de manière gamma, où le blanc, le noir, les gris et les points sur la référence de teinte J ne sont pas affectés. Tous les autres points tendent vers la référence de teinte J d’une manière lisse, se regroupe légèrement près de la référence de teinte J, la chroma restant constante. La dépendance chromatique garantit que les couleurs neutres ne sont pas affectées et que l’effet est accru sur les couleurs ayant une couleur plus élevée.

Voici une description mathématique de la compression de légèreté vers la référence de teinte J, ou de l’ajustement de la valeur J du point de destination. Il est appelé point de destination, car il a été mappé au gamut de destination.

Tout d’abord, calculez « factorC » (facteur de dépendance chromatique) pour le point de destination, ce qui détermine l’effet de la compression de légèreté. Les points proches ou sur l’axe J auront peu ou pas de compression ; les points plus éloignés de l’axe J (haute chromaie) auront plus de compression appliquée. Multipliez par 0,5 pour vous assurer que factorC est inférieur à 1, car il est possible que sourceC soit légèrement supérieur à référenceC, mais pas deux fois plus grand.

factorC = (destinationC / referenceC) ? 0.5

où :

destinationC est la valeur C du point de destination.

referenceC est la valeur C du point de référence Hue.

Ensuite, déterminez si le point de destination J est au-dessus ou au-dessous de la référence de teinte J. S’il est ci-dessus, procédez comme suit :

1. Calculez « factorJ » pour le point de destination par rapport à la référenceJ. Cette valeur factorJ sera comprise entre 0 et 1 (0 si sur la référenceJ; 1 si à maxJ).

2. factorJ = (destinationJ - référenceJ) / (maxJ - referenceJ)

   où :

   destinationJ est la valeur J du point de destination.

   referenceJ est la valeur J du point de référence hue.

   maxJ est la valeur J maximale du gamut.

3. Appliquez une fonction d’alimentation de type gamma à factorJ, ce qui réduit factorJ d’une certaine quantité. Cet exemple utilise la puissance de 2 (le carré). Soustrayez le facteur J réduit du facteur J d’origine et multipliez le résultat par la plage J totale au-dessus de la référence primaireJ pour rechercher le « deltaJ », qui représente la modification de J après la compression de légèreté, sans inclure la dépendance chromatique.

4. deltaJ = (factorJ - (factorJ ? factorJ)) ? (maxJ - referenceJ)

5. Appliquez factorC au deltaJ (plus la chroma est élevée, plus l’effet est important) et calculez la nouvelle valeur J pour le point de destination.

6. destinationJ = destinationJ - (deltaJ ? factorC)

Si la valeur J pour le point de destination se trouve sous référenceJ, un calcul similaire aux étapes précédentes A-C est effectué, en utilisant minJ au lieu de maxJ pour trouver la plage dans J pour calculer le facteurJ, et en tenant compte de la polarité des opérations « en dessous » de la référenceJ.

factorJ = (referenceJ - destinationJ) / (referenceJ - minJ)

deltaJ = (factorJ - (factorJ ? factorJ)) ? (referenceJ - minJ)

destinationJ = destinationJ + (deltaJ ? factorC)

où :

minJ est la valeur J minimale du gamut.

La chroma pour les points de couleur d’entrée est développée linéairement (si possible) le long de la luminosité constante proportionnelle à la valeur de chroma maximale des gamuts source et de destination à cette teinte et à cette légèreté. Combiné à la compression de légèreté dépendante des chromas précédente, cela permet de préserver la saturation, car le mappage de cisaillement à l’aide des points de référence entraîne parfois une compression excessive du point source dans la chroma (voir la figure 16).

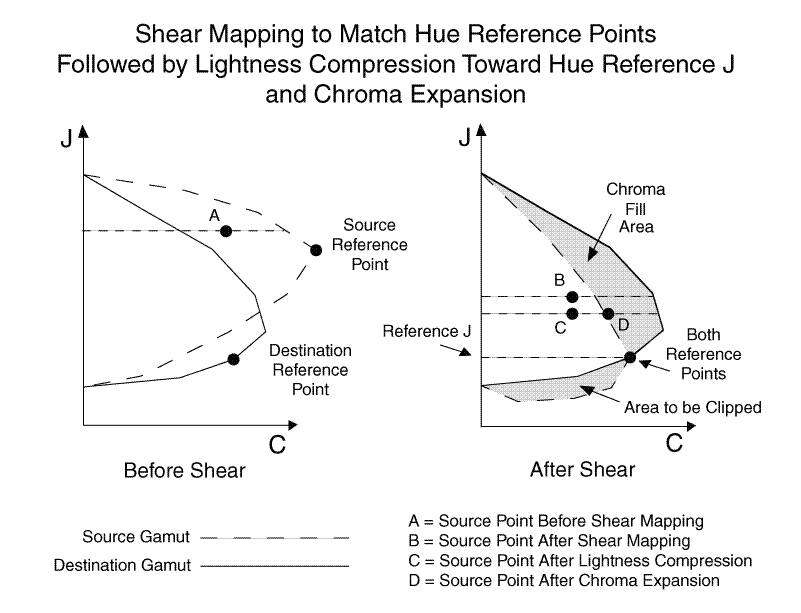
Figure 16 : Mappage de cisaillement, compression de la légèreté vers la référence de teinte J et expansion de la chroma

Voici une description mathématique du processus d’expansion chromatique ou l’ajustement de la valeur C du point de destination. Il est appelé point de destination, car il a été mappé et la légèreté compressée dans le gamut de destination.

1. Avant le mappage de cisaillement, déterminez sourceExtentC (l’étendue chromatique à la luminosité et à la teinte du point source).

2. Après le mappage de cisaillement et la compression de légèreté qui transforme le point source en point de destination, déterminez le destExtentC (l’étendue chromatique à la luminosité et à la teinte du point de destination).

3. Si la valeur sourceExtentC est supérieure à la valeur destExtentC, aucun ajustement chromatique du point de destination n’est nécessaire et vous pouvez ignorer l’étape suivante.

4. Ajustez destinationC (la chroma du point de destination) pour qu’il s’adapte à l’étendue chromatique de destination à cette légèreté et à cette teinte.

5. destinationC = destinationC ? (destExtentC / sourceExtentC)

   où :

   destinationC est la valeur C du point de destination.

   sourceExtentC est la valeur C maximale du gamut source à la luminosité et à la teinte du point source.

   destExtentC est la valeur C maximale du gamut de destination à la luminosité et à la teinte du point de destination.

Enfin, effectuez le découpage de distance mimimum. Si la couleur d’entrée pivotée, ajustée à la légèreté et mappée au cisaillement est toujours légèrement en dehors de la plage de destination, attachez-la (la déplacer) au point le plus proche de la limite de gamut de destination (voir figure 17).

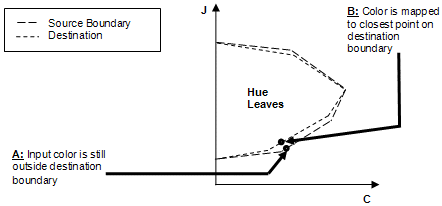
Figure 17 : Découpage de distance minimale

Description de la limite de gamut et algorithmes d’interpréteur de commandes Gamut

La fonction de limite de gamut d’appareil utilise le moteur de modèle d’appareil et les paramètres analytiques pour dériver une limite de gamut d’appareil de couleur, décrite comme une liste de vertex indexées de la coque de la gamut de l’appareil. La coque est calculée différemment selon que vous travaillez avec des appareils additifs, tels que des moniteurs et des projecteurs, ou des appareils soustractifs. La liste de vertex indexée est stockée dans CIEJab. La structure de la liste de vertex indexées est optimisée pour l’accélération matérielle par DirectX.

Cette approche propose de nombreuses solutions connues. Si vous recherchez « directX de coque convexe » sur le Web, vous obtenez plus de 100 coups. Par exemple, il existe une référence de 1983 sur ce sujet spécifique (Computer Graphics Theory and Application, « Shiphulls, b-spline surfaces, and cadcam », p. 34-49) avec des références datant de 1970 à 1982 sur le sujet.

La collection de points peut être déterminée à partir d’informations disponibles en externe, comme suit :

• Les points de l’interpréteur de commandes de référence pour les moniteurs sont générés à l’aide d’un échantillonnage du cube de couleur dans l’espace colorant de l’appareil.
• Des points pour l’interpréteur de commandes de référence pour les imprimantes et les périphériques de capture sont obtenus à partir des exemples de données utilisées pour initialiser le modèle.
• Les points de l’interpréteur de commandes de référence pour scRGB et sRGB sont générés à l’aide d’un échantillonnage du cube de couleur pour sRGB.
• Des points pour l’interpréteur de commandes plausible pour les appareils de capture sont générés à l’aide d’un échantillonnage du cube de couleur dans l’espace colorant de l’appareil.
• Des points pour l’interpréteur de commandes de référence pour les projecteurs sont générés à l’aide d’un échantillonnage d’un polyèdre dans le cube de couleur dans l’espace colorant de l’appareil.
• Des points pour l’interpréteur de commandes possible pour les espaces de couleurs à large plage dynamique sont générés à l’aide d’un échantillonnage du cube de couleur dans l’espace lui-même.

Vous pouvez créer une liste de vertex qui décrit efficacement la gamme de couleurs des appareils, en fonction d’un profil d’appareil et des services de support système.

Pour les appareils de sortie, la limite de gamut décrit la plage de couleurs qui peut être affichée par l’appareil. Une limite de gamut est générée à partir des mêmes données que celles utilisées pour modéliser le comportement de l’appareil. Conceptuellement, vous générez un échantillonnage de la plage de couleurs que l’appareil peut produire, mesurez les couleurs, convertissez les mesures en espace d’apparence, puis utilisez les résultats pour créer la limite de gamut.

Les périphériques d’entrée sont plus délicats. Chaque pixel d’une image d’entrée doit avoir une valeur. Chaque pixel doit être en mesure de représenter n’importe quelle couleur trouvée dans le monde réel d’une manière ou d’une autre. En ce sens, aucune couleur n’est « hors gamut » pour un appareil d’entrée, car elles peuvent toujours être représentées.

Tous les formats d’image numérique ont une plage dynamique fixe. En raison de cette limitation, il existe toujours des stimuli distincts qui correspondent à la même valeur numérique. Vous ne pouvez donc pas établir un mappage un-à-un entre les couleurs du monde réel et les valeurs d’appareil photo numérique. Au lieu de cela, la limite de gamut est formée en estimant une plage de couleurs réelles qui peuvent produire les réponses numériques de l’appareil photo. Vous utilisez cette plage estimée comme gamut pour le périphérique d’entrée.

Les primaires sont incluses pour fournir un mappage de gamut de type intention graphique métier.

Dans un style orienté objet vrai, vous abstraitz la représentation sous-jacente de la limite de gamut. Cela vous permet de modifier la représentation à l’avenir. Pour comprendre le descripteur de limite de gamut (GBD) utilisé dans le nouveau CTE, vous devez d’abord comprendre le fonctionnement des algorithmes de mappage de gamut (GMA). Traditionnellement, les GMA ont été conçus pour répondre aux besoins de la communauté des arts graphiques; autrement dit, pour reproduire des images qui ont déjà été correctement rendues pour l’appareil sur lequel l’image d’entrée a été créée. L’objectif des GMAs d’arts graphiques est d’obtenir la meilleure reproduction possible de l’image d’entrée sur l’appareil de sortie. Le nouveau GBD CTE est conçu pour résoudre quatre problèmes clés.

Étant donné que l’image d’entrée est rendue pour l’appareil d’entrée, toutes les couleurs s’inscrivent dans la plage entre le point blanc et le point noir du support. Supposons que l’image soit une photo d’une scène dans laquelle il y a un blanc diffus, comme une personne dans un tee-shirt blanc, et un surbrillance spéculaire, comme la lumière qui se reflète sur une fenêtre ou un pare-chocs chromé. La scène est rendue sur le support d’entrée afin que la mise en évidence spéculaire soit mappée au point blanc du milieu et que le blanc diffus soit mappé à une couleur neutre plus foncée que le point blanc du milieu. Le choix de la façon de mapper les couleurs de la scène au support d’entrée est à la fois une décision dépendante de la scène et une décision esthétique. Si le surbrillance spéculaire était absent de la scène d’origine, le blanc diffus serait probablement mappé au point blanc du support. Dans une scène avec beaucoup de détails en surbrillance, il reste plus de plage entre le blanc spéculaire et le blanc diffus. Dans une scène où la mise en évidence n’est pas significative, très peu de plage peut être laissée.

Pour les images pré-rendues, le mappage de gamuts est relativement simple. Fondamentalement, le point blanc du support d’origine est mappé au point blanc du support de reproduction, le point noir source est mappé au point noir de destination et la plupart du mappage est terminé. Les différents GMA existants fournissent des variations pour le mappage d’autres points sur l’échelle de tonalité du support source et différentes façons de gérer les valeurs de chroma hors gamut. Mais le mappage du blanc au blanc et du noir au noir est cohérent tout au long de ces variations. Cette implémentation nécessite que le blanc soit au-dessus d’un J* de 50 et le noir au-dessous d’un J* de 50.

Tous les encodages de couleurs ne limitent pas les plages de couleurs pour les images d’entrée. L’encodage de couleur standard IEC scRGB (IEC 61966-2-2) fournit 16 bits pour chacun des trois canaux de couleur rouge, vert et bleu (RVB). Dans cet encodage, le noir de référence n’est pas encodé en tant que triple RVB (0, 0, 0), mais en tant que (4096, 4096, 4096). Le blanc de référence est encodé comme (12288, 12288, 12288). L’encodage scRGB peut être utilisé pour représenter des surbrillances spéculaires et des détails d’ombre. Il comprend des triples RVB qui ne sont pas physiquement possibles, car ils nécessitent des quantités négatives de lumière et des encodages qui se trouvent en dehors du locus spectral CIE. De toute évidence, aucun appareil ne peut produire toutes les couleurs dans la gamut scRGB. En fait, aucun appareil ne peut produire toutes les couleurs qu’un être humain peut voir. Par conséquent, les appareils ne peuvent pas remplir la gamut scRGB, et il serait utile de pouvoir représenter la partie de la gamut qu’ils remplissent. Chaque appareil a une plage de valeurs dans l’espace scRGB qu’il peut produire. Il s’agit des couleurs « attendues » pour l’appareil ; il serait surprenant que l’appareil produise des couleurs en dehors de cette gamme. Il existe une transformation définie de l’espace scRGB en espace d’apparence, de sorte que chaque appareil a également une plage de valeurs d’apparence qu’il est censé reproduire.

Dans scRGB et l’entrée à partir d’appareils de capture caractérisés avec une cible fixe, il est possible d’obtenir une valeur en dehors de la plage des valeurs attendues. Si quelqu’un étalonne une caméra sur une cible de test ; et capture ensuite une scène avec des surbrillances spéculaires, il peut y avoir des pixels qui sont plus lumineux que le point blanc de la cible. La même chose peut se produire si un rouge naturel est plus chromatique que le rouge cible. Si quelqu’un prend une image scRGB à partir d’un appareil, puis modifie manuellement les couleurs de l’image, il est possible de créer des pixels qui se situent en dehors de la plage attendue de la gamut de l’appareil, même s’ils se trouvent dans la gamme scRGB complète.

Un deuxième problème ne semble pas, à première vue, être lié à cela. Cela se produit lorsque vous utilisez une cible de couleur pour caractériser un appareil d’entrée, tel qu’un appareil photo ou un scanneur. Les cibles réfléchissantes sont généralement produites sur papier et contiennent un certain nombre de patchs colorés. Les manufaturers fournissent des fichiers de données avec des mesures de couleur prises sous une condition d’affichage fixe pour chaque correctif de couleur. Les outils de profilage des couleurs créent un mappage entre ces valeurs mesurées et les valeurs retournées par les capteurs de couleur dans les appareils. Le problème est que souvent ces cibles de couleur ne couvrent pas la plage complète des valeurs de l’appareil. Par exemple, le scanneur ou l’appareil photo peut retourner une valeur de (253, 253, 253) pour le point blanc de référence, et un patch rouge de référence peut avoir une valeur RVB de (254, 12, 4). Elles représentent la plage de valeurs attendues pour l’appareil d’entrée, en fonction des valeurs cibles. Si vous caractérisez l’appareil d’entrée en fonction des réponses à la cible, vous n’attendez que des couleurs dans cette plage étroite. Cette plage n’est pas seulement plus petite que la plage de couleurs que les humains peuvent voir, elle est plus petite que la plage de couleurs que l’appareil peut produire.

Dans les deux cas, il est difficile d’estimer la gamut de l’appareil ou de l’image d’entrée, malgré l’existence d’une ou de mesures de référence. Dans le premier problème, la gamut plausible de l’appareil d’entrée est inférieure à la gamme complète de scRGB. Dans le deuxième problème, le gamut de référence de la cible est inférieur à la gamme complète possible de l’appareil d’entrée.

Le troisième problème concerne le mappage des tonalités. De nombreux modèles de limites de gamut qui peuvent représenter adéquatement des images pré-rendues utilisées dans les arts graphiques ont été proposés, par exemple, le GBD braun et Fairchild Mountain Range (Braun[97]) et le descripteur de limites segment maxima de Morovic (Morovic[98]). Mais ces modèles fournissent uniquement des informations sur les extrêmes de la gamme de l’appareil ; il manque des informations sur d’autres points dans le mappage tonal. Sans ces informations, les GMA ne peuvent que faire des estimations approximatives du mappage de tonalité optimal. Pire encore, ces modèles ne fournissent aucune aide pour la plage dynamique étendue dans scRGB et dans les images d’appareil photo numérique.

Comment ce problème est-il résolu dans les industries photographique et vidéographique ? L’appareil photo capture une image. Les experts peuvent débattre de la quantité de rendu qui se produit dans l’appareil de capture ; mais ils conviennent que ce n’est pas un montant significatif. Les deux technologies ne mappent pas un blanc diffus dans une scène capturée au point blanc du milieu. De même, ils ne mappent pas le point noir de la scène au point noir du milieu. Le comportement du film photographique est décrit dans l’espace de densité à l’aide d’une courbe caractéristique, souvent appelée Hurter et Driffield, ou courbe HD&. La courbe montre la densité de la scène d’origine et la densité résultante sur le film. La figure 18 montre une courbe HD&classique. L’axe x représente une exposition croissante du journal. L’axe y représente la densité sur la diapositive. Cinq points de référence sont marqués sur la courbe : noir sans détail, qui représente la densité minimale sur le négatif ; noir avec des détails; référencez les carte gris moyen ; blanc avec détail et blanc sans détail. Notez qu’il existe un espace entre le noir sans détail (qui représente le noir de l’appareil) et le noir avec des détails (noir ombre). De même, il existe un espace entre le blanc avec des détails (blanc diffus) et le blanc sans détail (qui représente le blanc de l’appareil).

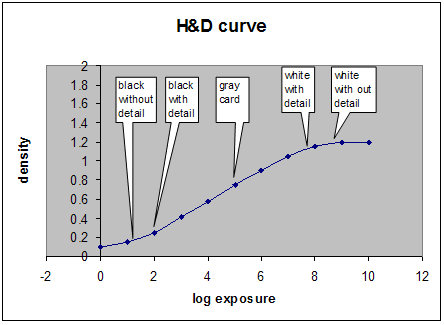
Figure 18 : Courbe HD&pour le film de diapositive

L’industrie de la vidéo fournit « headroom » et « footroom » dans les images. Dans la spécification ITU 709, la luminance (appelée Y) est encodée en 8 bits, avec une plage comprise entre 0 et 255. Toutefois, le noir de référence est encodé à 15 et le blanc de référence est encodé en 235. Cela laisse la plage d’encodage comprise entre 236 et 255 pour représenter les surbrillances spéculaires.

L’industrie vidéo présente un système de boucle essentiellement fermée. Bien qu’il existe de nombreux fournisseurs d’équipement différents, les systèmes vidéo sont basés sur des appareils de référence. Il existe un encodage standard pour les images vidéo. Il n’est pas nécessaire de communiquer une limite de gamut avec des images vidéo, car toutes les images sont encodées pour la reproduction sur le même appareil de référence. Film est également une boucle fermée, car il n’est pas nécessaire de transmettre des données intermédiaires entre différents composants. Vous souhaitez une solution qui permet de reproduire les images d’appareils avec des gamuts différents et représentant des scènes pré-rendues et non rendues sur sortie avec des gamuts variables.

Un quatrième problème que le nouveau CTE doit résoudre est que les couleurs visuellement grises produites par un appareil, par exemple, quand rouge=vert=bleu sur un moniteur, ne tombent souvent pas sur l’axe neutre du CAM (lorsque la chromaie = 0,0). Cela entraîne de grandes difficultés pour les GMA. Pour que les GMA fonctionnent correctement, vous devez ajuster la description de la gamme de l’appareil et des points d’entrée afin que l’axe neutre de l’appareil tombe sur l’axe neutre de l’espace d’apparence. Vous devez ajuster les points hors de l’axe neutre d’un montant similaire. Sinon, vous ne pouvez pas effectuer de gradations fluides via l’image. En sortant de la GMA, vous annulez ce mappage par rapport à l’axe neutre de l’appareil de sortie. Il s’agit d’un redressement « chiropratique » de l’axe. Comme un chiropraticien, non seulement vous redressez le squelette (axe neutre), mais vous ajustez le reste du corps pour se déplacer avec le squelette. Comme un chiropraticien, vous n’ajustez pas le squelette de la même quantité à travers tout l’espace. Au lieu de cela, vous ajustez les différentes sections différemment.

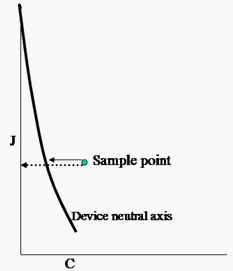
Figure 19 : Courbure de l’axe neutre de l’appareil par rapport à l’axe neutre CIECAM

Le nouveau CTE nécessite un modèle de limite de gamut qui peut être utilisé pour représenter à la fois des images sources rendues et non rendues, fournir des informations sur l’apparence des neutres d’appareil et fournir des informations pour le mappage de tonalités avec une large plage de luminance.

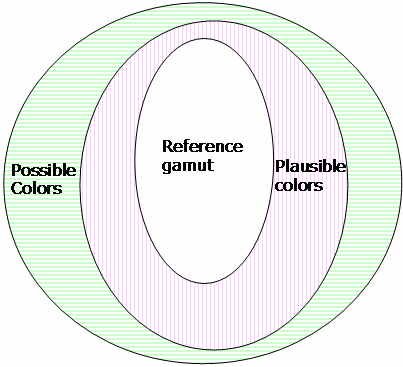
Figure 20 : Trois interpréteurs de commandes gamut

La limite de gamut est composée de trois interpréteurs de commandes qui définissent trois régions.

Dans le nouveau CTE, l’enveloppe externe du gamut est formée avec une coque convexe faite à partir de points d’échantillon dans la gamut de l’appareil. Une coque est formée en prenant un ensemble de points d’échantillonnage et en les entourant par une surface. Une coque convexe a la propriété supplémentaire d’être convexe partout. Par conséquent, il ne s’agit pas de la plus petite coque possible qui peut être adaptée aux données. Mais l’expérimentation a montré que l’ajustement trop serré des points d’échantillon entraîne des artefacts peu appétissants dans les images, comme un manque de trame lisse. La coque convexe semble résoudre ces problèmes.

Dans l’algorithme, les valeurs d’apparence de couleur sont obtenues pour un ensemble de points échantillonné à partir de l’appareil. Pour les moniteurs et les imprimantes, les valeurs d’apparence des couleurs sont obtenues en sortant des échantillons, puis en les mesurant. Vous pouvez également créer un modèle d’appareil, puis exécuter des données synthétiques via le modèle d’appareil pour prédire les valeurs mesurées. Les valeurs mesurées sont ensuite converties de l’espace colorimétrique (XYZ) en espace d’apparence (Jab), et la coque est encapsulée autour des points.

Le point clé de cet algorithme est que le point blanc adopté utilisé dans la conversion de l’espace colorimétrique en espace d’apparence n’a pas besoin d’être le point blanc du support. Au lieu de cela, vous pouvez sélectionner un point plus loin à l’intérieur de la gamme et sur (ou près) de l’axe neutre. Ce point aura alors une valeur J de 100. Les échantillons dont la valeur Y mesurée est supérieure au point blanc adopté se retrouvent avec une valeur J supérieure à 100.

Si vous placez le point blanc diffus de la scène comme point blanc adopté pour la conversion de l’espace de couleurs, les surbrillances spéculaires dans la scène seront facilement détectées comme ayant une valeur J supérieure à 100.

Étant donné que le modèle de couleur CIECAM02 est basé sur le système visuel humain, une fois qu’un blanc adopté est sélectionné, le niveau de luminance du point noir (J = 0) est automatiquement déterminé par le modèle. Si l’image d’entrée a une large plage dynamique, il est possible qu’il y ait des valeurs qui mappent à des valeurs J inférieures à zéro.

La figure 21 suivante montre les appareils neutres qui s’exécutent au centre des gamuts plausibles et de référence.

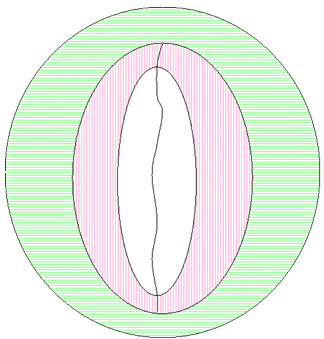
Figure 21 : Axe neutre de l’appareil ajouté à la limite de gamut

Tous les mappages de gamut impliquent soit de couper une plage d’entrée sur un gamut de sortie, soit de compresser le gamut d’entrée pour qu’il s’adapte au gamut de sortie. Des algorithmes plus complexes sont formés en compressant et en coupant dans différentes directions, ou en divisant la gamut en différentes régions, puis en effectuant un découpage ou une compression dans les différentes régions.

Le nouveau CTE étend ce concept pour prendre en charge les régions d’un gamut possible, d’un gamut plausible et d’un gamut de référence, et permet aux GMA de les mapper de différentes manières. En outre, les GMA disposent d’informations sur l’axe neutre de l’appareil. La discussion suivante explique comment gérer les situations où les gamuts plausibles et les gamuts de référence se sont réduits les uns sur les autres.

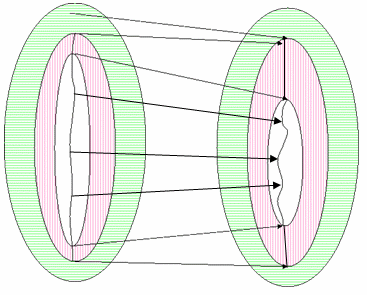
Figure 22 : GMA avec deux descripteurs gamut non réduits

Vous pouvez voir cet exemple si vous mappez à partir d’un périphérique d’entrée, tel qu’un appareil photo ou un scanneur caractérisé par une cible réfléchissante, à l’espace scRGB. Ici, les couleurs plausibles qui sont plus claires que le blanc de référence sont des surbrillances spéculaires. Dans la pratique, la caractérisation d’une caméra avec une cible peut ne pas générer la plage complète de valeurs possible dans la caméra ; cependant, les surbrillances spéculaires et les couleurs très chromatiques trouvées dans la nature le feraient. (Les cibles transmissives ont généralement un patch qui correspond à la densité minimale possible sur le milieu. Avec une telle cible, les surbrillances spéculaires se situent dans la plage de la cible.) Le noir de référence pour une cible réfléchissante serait le début de la zone noire d’ombre. Autrement dit, il est probable que les couleurs des ombres soient plus foncées que le noir sur la cible. Si l’image contient beaucoup de contenu intéressant dans cette région, il peut être utile de conserver cette variation tonale.

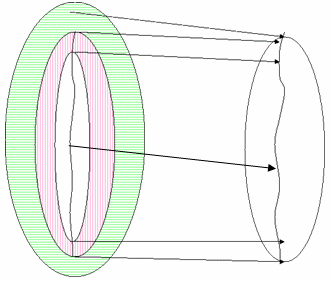
Figure 23 : GMA avec gamut de destination réduit

La figure 23 montre un algorithme de mappage de gamut possible lorsque le gamut de destination fournit uniquement la plage du blanc de l’appareil au noir, et qu’il n’existe aucune couleur possible en dehors de cette gamut. Cela est susceptible de se produire pour les périphériques de sortie classiques, tels que les imprimantes. Les couleurs possibles sont mappées au bord du gamut de destination. Mais il manque une courbe de tonalité pour l’appareil de sortie. La GMA doit sélectionner un point neutre de luminance inférieure à utiliser comme destination de mappage pour le blanc de référence. Un algorithme sophistiqué peut le faire en histogramme les légèretés dans l’image source et en voyant combien tombent dans la plage attendue mais plus claire que le blanc de référence. Plus il y a de légèreté, plus l’appareil de destination nécessite d’espace entre les points mappés pour les surbrillances spéculaires et le blanc de référence. Un algorithme plus simple peut choisir une distance arbitraire vers le bas de l’échelle de luminosité à partir du blanc de l’appareil, par exemple 5 %. Une approche similaire s’applique au mappage du noir maximal et du noir d’ombre.

Après avoir généré la courbe de tonalité de destination, vous pouvez mapper dans une méthode similaire à celle utilisée dans la figure 23 précédente. Tous les points de la courbe de tonalité de destination se situent dans le gamut de l’appareil, et tous les points du mappage doivent se trouver dans le gamut de l’appareil.

Si vous inversez les figures de gauche et de droite, ainsi que les directions des flèches de la figure 23, vous pouvez décrire le cas où l’image source n’a qu’un gamut de référence, et où les trois gamuts de l’appareil de sortie ne se sont pas réduits les uns sur les autres. Un exemple de ceci peut être le mappage d’un moniteur à scRGB. Là encore, la GMA doit synthétiser les points de contrôle des cinq points de la courbe de tonalité de l’image source. Certains mappages peuvent placer tous les points de la courbe de tonalité dans le gamut d’appareil scRGB, tandis que d’autres mappages peuvent utiliser davantage de la gamut scRGB en mappant le blanc diffus au blanc de référence et en autorisant le blanc spéculaire à mapper à une valeur plus claire.

Enfin, vous avez le cas où les deux appareils ont uniquement le gamut de référence, ce qui est la façon dont la plupart des algorithmes de mappage de gamut fonctionnent. Vous pouvez donc résoudre ce problème en revenir simplement aux algorithmes actuels. Si vous disposez d’un moyen raisonnable de déterminer les cinq points de référence pour les appareils source et de destination, vous pouvez également vous organiser pour mapper les points de référence.

Les gamuts d’appareils contiennent plus que les cinq points de référence sur l’axe neutre. Celles-ci représentent simplement les limites entre les régions potentielles dans l’image. Entre chacun des points de référence, vous pouvez utiliser l’une des techniques de mappage de gamut existantes. Ainsi, vous pouvez couper la plage de couleurs inattendues et compresser toutes les couleurs entre le blanc et le noir attendu, ou vous pouvez couper toutes les couleurs en dehors de la plage de référence et compresser dans cette plage. Il existe de nombreuses possibilités, qui peuvent être mises en œuvre dans différents GMA. De plus, les MGM peuvent compresser et couper de différentes manières. Toutes ces combinaisons sont couvertes par cette invention.

Jusqu’à présent, dans cette discussion, la gamut a été traitée comme s’il s’agissait uniquement d’une fonction de l’appareil sur lequel l’image a été créée, capturée ou affichée. Toutefois, il n’y a aucune raison pour que toutes les images d’un appareil aient la même gamut. Les GMA dépendent des données dans le GBD. Si le descripteur est modifié d’une image à l’autre, il n’y a aucun moyen pour les GMAs de le savoir. En particulier, si les images n’ont pas de surbrillances spéculaires, les MGM fonctionnent mieux si le descripteur gamut ne montre pas qu’il existe des couleurs plus claires que le blanc diffus.

Dans la nouvelle architecture CTE, il est possible d’utiliser plusieurs GMA. L’utilisation de plusieurs GMA est intrinsèquement mal définie. Par exemple, si un appareil de capture associe une GMA à son « apparence », il a tendance à le faire avec un gamut de destination « ciblé ». Il en va de même pour les appareils de sortie et les gamuts sources « ciblés ». Le gamut sRGB est un gamut implicite fréquemment ciblé. Par conséquent, il est fortement recommandé d’utiliser une seule GMA, si la prévisibilité est une priorité. Un flux de travail GMA unique doit être la valeur par défaut pour tous les flux de travail, en particulier les workflows de consommateurs et de prosommateurs. Bien que le mappage de gamut pour la reproduction préférée doit être effectué une seule fois, il existe des cas où plusieurs processus de mappage sont inclus. Tout d’abord, pour la vérification linguistique, vous effectuez un mappage préféré au gamut de l’appareil cible final, puis un rendu colorimétrique sur le gamut de l’appareil de vérification linguistique. Deuxièmement, certains types de mappage sont utilisés pour modifier les caractéristiques de l’image, mais ne sont pas inclus pour mapper à un gamut d’appareil, par exemple, en ajustant la courbe de tonalité ou la chromaticité. Si plusieurs GMA sont utilisés, l’interface de transformation prend un tableau de cartes de gamut liées, c’est-à-dire des cartes de gamut qui ont été initialisées avec une paire de descriptions de limites de gamut. Lorsqu’il existe plusieurs mappages de gamut, la limite de gamut d’entrée d’une carte de gamuts suivante doit être identique à la limite de gamut de sortie de son prédécesseur.

La fonction de limite de gamut d’appareil prend le moteur du modèle d’appareil et les paramètres analytiques et dérive une limite de gamut d’appareil de couleur décrite comme une liste de vertex ordonnée de la coque convexe de la gamut de l’appareil. La liste de vertex ordonnée est stockée dans CIEJab. La structure de la liste de vertex ordonnée est optimisée pour l’accélération matérielle par DirectX. Cette approche a de nombreuses solutions bien connues (recherchez « directX de coque convexe » sur le web et vous obtenez plus de 100 coups). Il existe également une référence de 1983 sur ce sujet (Computer Graphics Theory and Application, « Shiphulls, b-spline surfaces and cadcam » pp. 34-49), avec des références datant de 1970 à 1982 sur le sujet.

Deux techniques différentes peuvent être utilisées pour calculer les triangles dans l’interpréteur de commandes gamut. Pour d’autres appareils que les appareils RVB additifs, vous calculez une coque convexe. Vous pouvez envisager d’examiner la prise en charge de la coque non convexe pour d’autres appareils si vous avez un accès direct à ces appareils pour valider la robustesse, les performances et la fidélité des algorithmes. Il s’agit d’un processus bien connu qui ne nécessite pas de description supplémentaire. La technique utilisée pour les appareils RVB additifs est décrite comme suit.

Différents GBD présentent des avantages et des inconvénients. La représentation de coque convexe garantit de belles propriétés géométriques, telles que des tranches de teinte convexe qui fournissent un point d’intersection unique avec un rayon émanant d’un point sur l’axe neutre. L’inconvénient de la représentation de la coque convexe est également la convexité. Il est connu que de nombreux appareils, en particulier les appareils d’affichage, ont des gamuts qui sont loin d’être convexes. Si le gamut réel s’écarte considérablement de l’hypothèse de convexité, la représentation de la coque convexe serait inexacte, peut-être dans la mesure où elle ne représente pas la réalité.

Après avoir adopté un GBD qui donne une représentation assez précise de la gamut réelle, d’autres problèmes se posent, certains en raison du concept même de tranche de teinte. Il existe au moins deux situations pathologiques. Dans la figure 24 suivante, une gamme CRT donne lieu à des tranches de teinte avec des « îlots ». Dans la figure 25, un gamut d’imprimante donne lieu à une tranche de teinte avec une partie de l’axe neutre manquante. Les tranches de teinte pathologique ne sont pas causées par des limites de gamut particulièrement pathologiques dans ces cas. Elles sont provoquées par le concept même de tranche de teinte, car (a) elle est prise le long de la teinte constante, et (b) elle ne prend qu’une moitié du plan qui correspond à l’angle de teinte.

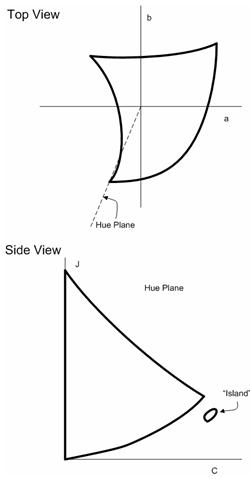
Figure 24 : Un moniteur CRT classique a un gamut qui montre une « courbure » particulière dans les teintes bleues. Si des tranches de teinte sont prises dans cette plage de teintes, des îlots isolés peuvent apparaître dans les tranches de teinte.

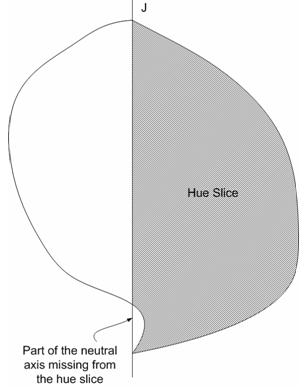
Figure 25 : Une imprimante peut avoir un gamut dont l’axe neutre est « gap ». Lorsqu’une tranche de teinte est prise (qui n’est qu’une moitié du plan), il y a une « dent » sur la partie de la limite qui est l’axe neutre. Cela peut être difficile à résoudre de manière algorithmique.

Pour résoudre ces pathologies, un nouveau framework est proposé qui abandonne le concept de tranche de teinte utilisé comme point de départ. Au lieu de cela, l’infrastructure utilise l’ensemble des « éléments de ligne de limite », ou des lignes qui se trouvent sur la limite de gamut. Ils ne fournissent pas nécessairement une visualisation géométrique cohérente comme les tranches de teinte, mais ils prennent en charge toutes les opérations de gamut courantes. En plus de résoudre les problèmes mentionnés précédemment, cette approche suggère également que la construction de tranches de teintes, même lorsqu’elle est possible, est un gaspillage de calcul.

Triangulation de la limite gamut

Le point de départ est un GBD constitué d’une triangulation de la limite de gamut. Les méthodes connues de construction de GBD fournissent généralement cette triangulation. Pour plus de détails, une méthode de construction de GBD pour les appareils additifs son espace d’appareil est décrite ici. Ces appareils incluent des moniteurs (crt et LCD) et des projecteurs. La géométrie simple du cube vous permet d’introduire un réseau régulier sur le cube. Les faces limites du cube peuvent être triangulées de plusieurs manières, comme celle illustrée dans la figure 26. L’architecture fournit un modèle d’appareil pour l’appareil afin que les valeurs colorimétriques des points de réseau puissent être obtenues de manière algorithmique, ou des mesures ont été effectuées directement pour ces points. L’architecture fournit également CIECAM02, de sorte que vous pouvez supposer que les données de démarrage ont déjà été mappées dans l’espace Jab CIECAM02. Ensuite, chaque point de réseau sur les faces limites du cube RVB a un point correspondant dans l’espace Jab. Les connexions de points qui forment l’ensemble des triangles dans l’espace RVB induisent également un ensemble de triangles dans l’espace Jab. Cet ensemble de triangles forme une triangulation raisonnable de la limite de gamut si (a) le réseau du cube RVB est suffisamment fin et (b) la transformation de l’espace de l’appareil en espace de couleurs uniforme est topologiquement bien conduite ; autrement dit, il mappe la limite à la limite, et il ne tourne pas la gamut à l’intérieur vers l’extérieur de sorte que les points intérieurs deviennent des points limites.

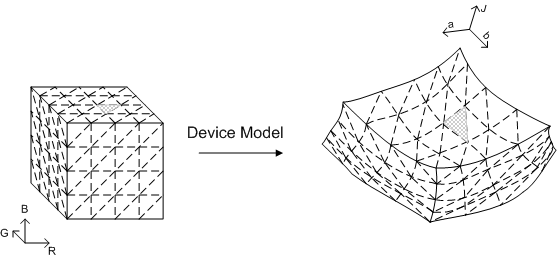
Figure 26 : Méthode simple pour trianguler la limite de gamut d’un appareil avec RVB comme espace d’appareil

Éléments de ligne de limite

Le concept d’éléments de ligne de limite est central dans ce framework ; ensemble de segments de ligne qui (a) se trouvent sur la limite de gamut et (b) se trouvent sur un plan. Dans ce cas, le plan est un plan de teinte. Chaque segment de ligne est le résultat de l’intersection du plan avec un triangle de limite de gamut. Bien que de nombreux chercheurs aient utilisé la construction de l’intersection d’un plan avec des triangles limites, ils analysent généralement la relation entre ces segments de trait et tentent de construire un objet géométrique cohérent à partir des segments de ligne. Différents algorithmes ont été conçus pour suivre ces segments de ligne les uns après les autres jusqu’à ce qu’une tranche de teinte entière soit obtenue, et de nombreuses tentatives ont été effectuées pour accélérer le processus de recherche.

Cette approche est différente. Vous croisez le plan avec les triangles pour obtenir les segments de ligne. Vous considérez ensuite ces segments de ligne comme les objets conceptuels de base . Il est nécessaire d’analyser la relation entre les segments de ligne ; vous n’avez pas besoin de savoir comment ils sont interconnectés les uns avec les autres. Ce point de vue résout le problème de la tranche de teinte avec des îlots. Les approches connues qui tentent de construire une tranche de teinte supposent que, si l’on commence par un segment de ligne et le suit jusqu’au segment de ligne suivant, et ainsi de suite ; il finit par revenir au point de départ, à partir duquel une tranche de teinte entière serait construite. Malheureusement, cette approche manquerait l’île (et dans le pire des scénarios, le continent). En n’insistant pas sur l’obtention d’une image géométrique cohérente; c’est-à-dire, tranche de teinte, vous pouvez gérer le problème d’île sans effort. Une autre différence importante dans cette approche est que, pour accélérer la construction des segments de ligne, elle utilise un « filtre triangle ». Le filtre triangle supprime certains triangles qui ne produiront certainement pas de segments de ligne qui seraient utiles dans l’opération de gamut actuelle. Étant donné que l’intersection d’un triangle avec le plan est coûteuse en calcul, cela améliore la vitesse. Un effet secondaire est que vous ne pouvez pas construire de tranche de teinte, car certains segments de ligne seraient manquants en raison du filtrage de triangle.

Opération Gamut : CheckGamut

L’exemple suivant explique comment fonctionne l’infrastructure et comment CheckGamut est effectué, c’est-à-dire l’opération de vérification si une couleur est in-gamut.

L’infrastructure générale est illustrée dans la figure 27 suivante. Il existe différents composants. Les composants étiquetés en italique sont des composants qui peuvent être différents dans l’implémentation en fonction de l’opération gamut en question. Les autres composants sont invariants pour toutes les opérations de gamut. Pour commencer, l’entrée est un ensemble d’attributs de couleur. Dans le cas de CheckGamut, il s’agit de la couleur de la requête. Dans la figure 27 et la discussion suivante, il est supposé que l’angle de teinte fait partie des attributs de couleur d’entrée ou peut être obtenu à partir de ceux-ci. C’est clairement le cas si l’entrée est le point de couleur entier, soit dans Jab ou JCh, à partir duquel vous pouvez calculer l’angle de teinte. Notez que l’angle de teinte n’est nécessaire que parce que des plans de teinte sont utilisés. Selon l’opération de gamut en question, il peut ne pas être nécessaire d’utiliser le plan de teinte. Par exemple, dans la construction de la routine CheckGamut, vous pouvez utiliser des plans de J constant. Il s’agit d’une généralité qui ne sera pas utilisée ni abordée plus en détail; mais il peut être utile de rappeler cette flexibilité de la méthodologie pour prendre en charge d’autres opérations de gamut lorsque le plan de teinte n’est peut-être pas le meilleur choix.

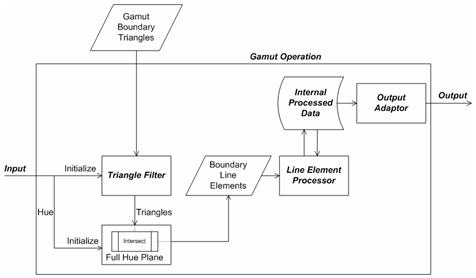
Figure 27 : Infrastructure pour prendre en charge les opérations gamut

L’angle de teinte, qui est obtenu directement à partir des entrées ou calculé à partir des entrées, est utilisé pour initialiser le plan de teinte étiqueté Plan hue complet dans la figure. « Full » est souligné parce que c’est le plan complet, pas seulement le demi-plan contenant la teinte. Le plan complet contient à la fois l’angle de teinte d’entrée et l’angle de 180 degrés qui lui est opposé. La fonctionnalité clé du plan hue est la fonction Intersect, qui est expliquée dans la sous-section suivante, Full Hue Plane: Intersect. Supposons que le GBD a déjà été construit et que l’ensemble de triangles de limites gamut est disponible. Croisez les triangles qui ont survécu au filtre triangle avec le plan de teinte à l’aide de l’intersection. Le composant Filtre triangle est étiqueté en italique, ce qui signifie que le composant varie en implémentation pour différentes opérations de gamut. Le filtre triangle pour CheckGamut est expliqué dans la section Opération Gamut : CheckGamut (suite). Le résultat de l’intersection d’un triangle avec le plan de teinte est soit vide, soit un élément de ligne limite , c’est-à-dire une paire de points distincts. Si le résultat n’est pas vide, il est passé dans le processeur d’éléments de ligne , qui effectue à nouveau des opérations différentes en fonction de l’opération gamut. Le processeur d’éléments de ligne met à jour la structure de données interne, Données traitées internes , dont le contenu ou la disposition dépend également de l’opération gamut. En règle générale, les données traitées internes contiennent la « réponse » au problème, qui est continuellement mise à jour avec chaque nouvel élément de ligne de limite trouvé. Lorsque tous les éléments de ligne de limite ont été traités, la réponse a été trouvée. Il reste à y accéder via l’adaptateur de sortie. Étant donné que les données traitées internes sont spécifiques à l’opération gamut, l’adaptateur de sortie est également spécifique à l’opération de gamut.

Plan Hue complet : intersecter

La fonction Intersect calcule l’intersection du plan de teinte et d’un triangle. Aussi simple que cela puisse paraître, cette fonction est importante pour deux raisons.

Tout d’abord, l’intersection de chaque bord du triangle avec le plan peut produire trois points d’intersection, une situation géométriquement impossible. La raison pour laquelle cela peut se produire dans le calcul est que, lorsque les calculs sont effectués en virgule flottante, par exemple au format IEEE, il existe des incertitudes, ou « bruit numérique », dans chaque étape qui affecte la conclusion de si un bord croise le plan. Lorsque le plan croise les bords dans une situation de quasi-absence, les points d’intersection sont proches les uns des autres et la détermination si un point d’intersection se trouve à l’intérieur du bord est aléatoire. Bien que le bruit dans les valeurs numériques des points soit faible, la conclusion qualitative selon laquelle il y a plus de deux points d’intersection est géométriquement impossible et difficile à gérer correctement dans l’algorithme.

Deuxièmement, cette fonction se trouve dans la boucle critique pour chaque bord de chaque triangle filtré. Il est donc important d’optimiser son efficacité autant que possible.

Pour résoudre le premier problème de bruit numérique, effectuez les calculs en entiers. Pour résoudre le deuxième problème d’optimisation de son efficacité, mettez en cache l’attribut le plus utilisé de chaque sommet, ou le « produit point » associé à chaque sommet. Le passage en entiers est un moyen classique de garantir la cohérence géométrique. L’idée de base est que si vous devez quantifier, faites-le au début. Ensuite, les calculs suivants peuvent être effectués en entiers, et si les entiers sont suffisamment larges pour qu’il n’y ait aucun risque de dépassement de capacité, les calculs peuvent être effectués avec une précision infinie. La fonction de quantification suivante est utile à cet effet.

ScaleAndTruncate(x) = Partie entière de x*10000

Le facteur de mise à l’échelle 10000 signifie que le nombre à virgule flottante d’entrée a quatre décimales, ce qui est suffisamment précis pour cette application. En fonction de la plage de valeurs de l’espace d’apparence de couleur, vous souhaitez choisir un type entier avec des bits suffisamment larges pour contenir les calculs intermédiaires. Dans la plupart des espaces d’apparence de couleur, la plage de chaque coordonnée est comprise entre -1 000 et 1 000. La coordonnée quantifiée a une valeur absolue maximale possible de 1 000 *10 000 = 10 000 000. Comme vous le verrez, la quantité intermédiaire est un produit à points, qui est une somme de deux produits de coordonnées, de sorte qu’elle a une valeur absolue maximale possible de 2* (10 000 000) ₂ = 2?10 ₁₄. Le nombre de bits requis est log ₂ (2?10 ₁₄ ) = 47,51. Un choix pratique pour le type entier est donc des entiers 64 bits.

Pour garantir que l’intersection d’un plan avec un triangle donne toujours un ensemble vide ou un ensemble de deux points, vous devez considérer le triangle comme un ensemble, et non comme des bords individuels du triangle séparément. Pour comprendre la situation géométrique, considérez les « distances signées » des sommets du triangle du plan de teinte. Ne calculez pas ces distances signées directement ; au lieu de cela, calculez les produits de points des vecteurs de position des sommets avec le vecteur normal quantifié vers le plan. Plus précisément, lors de l’initialisation du plan de teinte, le vecteur normal quantifié est calculé comme suit.

NormalVector = (ScaleAndTruncate(-sin(hue)), ScaleAndTruncate(cos(hue)))

Notez que ce vecteur est un vecteur à deux dimensions. Vous pouvez utiliser un vecteur à deux dimensions, car le plan de teinte est vertical, de sorte que le troisième composant du vecteur normal est toujours égal à zéro. En outre, une table de recherche de produits à points est initialisée pour avoir une entrée pour chaque sommet à partir des triangles de limites gamut et le produit à points correspondant défini sur une valeur non valide.

Lors d’une opération d’intersection du plan de teinte avec un triangle, le produit de points de chaque sommet du triangle est recherché. Si la valeur de la table de recherche est la valeur non valide, le produit point est calculé à l’aide de l’expression suivante.

NormalVector.a*ScaleAndTruncate(vertex.a) + NormalVector.b*ScaleAndTruncate(vertex.b)

Là encore, le composant J du vertex n’est jamais utilisé, car le vecteur normal est horizontal. Ce produit à points est ensuite enregistré dans la table de recherche afin qu’il n’ait pas besoin d’être calculé à nouveau si le produit point du vertex est interrogé ultérieurement.

La mise en cache permet de déterminer rapidement si un bord croise le plan, une fois que les produits point ont été tabulés dans la table de recherche, qui est générée progressivement au fur et à mesure que les sommets sont traités.

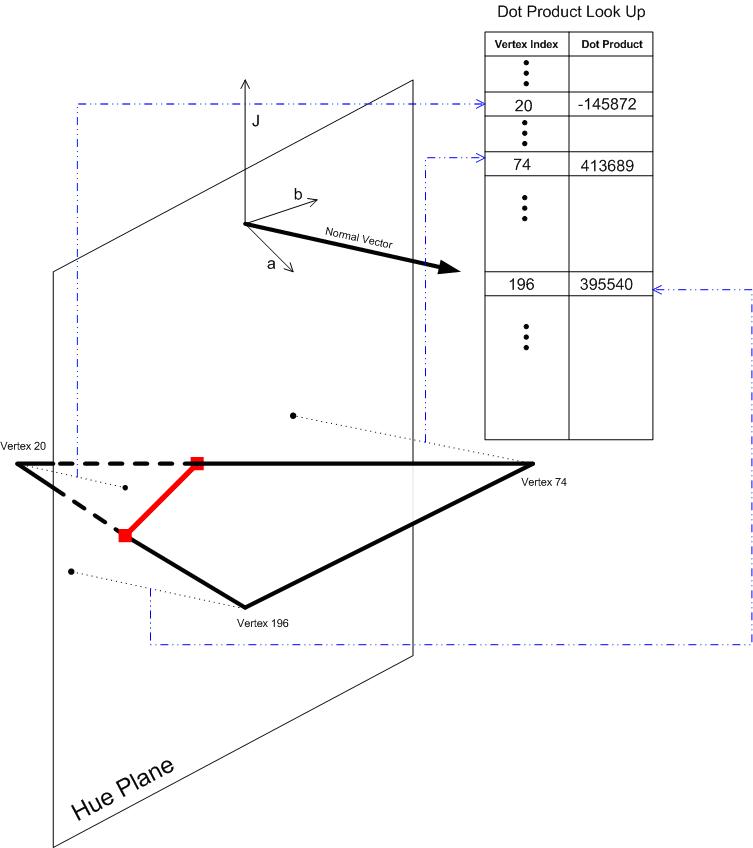
Figure 28 : Intersection du plan de teinte avec un triangle

Pour que le triangle de la figure 28 croise le plan de teinte dans un segment de ligne non dégénéré, les produits de points des sommets doivent être dans l’un des modèles suivants, lorsqu’ils sont triés dans l’ordre croissant.

0,0,+; -,0,0; -,0,+; -,-,+; -,+,+

Un point de terminaison du segment de ligne apparaît lorsque le plan est croisé par un bord avec des sommets qui ont des signes différents dans le produit point. Si le signe est égal à zéro, le sommet se trouve à droite sur le plan, et l’intersection du bord avec le plan est le sommet lui-même. Notez également que les cas 0,0,0; -,-,0; 0,+,+ ne sont pas signalés. Le premier cas (0,0,0) signifie que l’ensemble du triangle se trouve sur le plan. Cela n’est pas signalé, car chaque bord du triangle doit appartenir à un triangle voisin qui ne se trouve pas également entièrement sur le plan. L’arête est signalée lorsque ce triangle est pris en compte. Les deux autres cas (-,-,0 et 0,++) correspondent à la configuration géométrique selon laquelle le triangle touche le plan dans un sommet. Ces cas ne sont pas signalés, car ils ne donnent pas lieu à un segment de ligne non dégénéré.

L’algorithme précédent détermine quand calculer une intersection entre un bord du triangle et le plan de teinte. Une fois qu’un bord est déterminé, l’intersection est calculée à l’aide d’équations paramétriques. Si l’un des produits à points est égal à zéro, l’intersection est le sommet lui-même, donc aucun calcul n’est nécessaire. En supposant que les deux produits à points des sommets du bord sont non nuls , vertex1 est le vertex avec point négatif produit dotProduct1; et vertex2 est le sommet avec point positif produit dotProduct2. Cet ordre est important pour s’assurer que le point d’intersection calculé ne dépend pas de la façon dont l’ordre des sommets apparaît dans la représentation de l’arête. Le concept géométrique du bord est symétrique par rapport à ses sommets. L’aspect informatique de l’utilisation d’équations paramétriques du bord introduit une asymétrie (choix du sommet de départ), qui peut donner un point d’intersection légèrement différent en raison du bruit numérique et du conditionnement des équations linéaires à résoudre. Ceci étant dit, le point d’intersection, intersection, est donné par ce qui suit.

t = dotProduct1/(dotProduct1 - dotProduct2)

Intersection. J = vertex1. J + t * (vertex2. J - vertex1. J)

intersection.a = vertex1.a + t * (vertex2.a - vertex1.a)

intersection.b = vertex1.b + t * (vertex2.b - vertex1.b)

Opération Gamut : CheckGamut (suite)

L’algorithme géométrique de base utilisé pour la vérification de la gamut consiste à compter le nombre de croisements de rayons. Pour un point de requête donné, envisagez un rayon commençant par le point de requête et pointant vers le haut (direction J). Comptez le nombre de fois où ce rayon franchit la limite de gamut. Si ce nombre est pair, le point de requête est hors gamut. Si ce nombre est impair, le point se trouve à l’intérieur. En principe, cet algorithme peut être implémenté en 3D, il est généralement en proie à des difficultés causées par des situations dégénérées, telles que le rayon se trouve (en partie) sur un triangle de limite, ou une dégénération de dimension inférieure, comme le rayon qui se trouve (en partie) sur un bord d’un triangle limite. Même en 2D, vous devez faire face à ces situations dégénérées; mais le problème est plus simple et a été traité de manière satisfaisante. Voir [O’Rourke].

Pour un point d’entrée donné Jab, déterminez son angle de teinte h comme suit.

h = atan(b/a),

Initialisez le plan de teinte, puis déterminez les éléments de ligne limite correspondant à ce plan de teinte. Étant donné que les éléments de ligne limite ne sont pertinents que s’ils croisent le rayon vers le haut, configurez un filtre triangle pour supprimer les triangles qui donnent des éléments de ligne qui ne croiseront certainement pas le rayon vers le haut. Dans ce cas, considérez le cadre englobant du triangle. Le rayon vers le haut n’entrecroisera pas le triangle si le point de requête se trouve en dehors de l'« ombre » projetée par le cadre englobant si une source de lumière se trouvait directement au-dessus. Gonflez légèrement cette valeur avec une tolérance prédéfinie pour permettre le bruit numérique afin de ne pas jeter par inadvertance des triangles qui pourraient donner des éléments de trait utiles. Le résultat est le cylindre rectangulaire semi-infini illustré dans la figure 29. Vérifier si le point de requête se trouve à l’intérieur ou à l’extérieur de ce cylindre peut être implémenté efficacement à l’aide de simples inégalités.

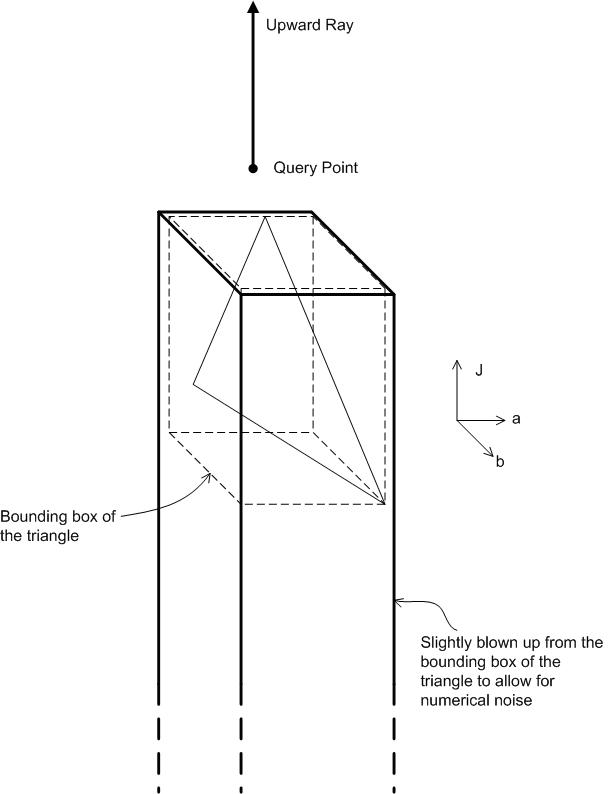
Figure 29 : Filtre triangle pour CheckGamut

CheckGamut comporte trois composants spécifiques aux opérations de gamut : Données traitées internes, Processeur d’éléments de ligne et Adaptateur de sortie. Les données traitées internes sont une liste d’éléments de ligne qui ont été traités par le processeur d’éléments de ligne. Dans ce cas, le processeur d’éléments de ligne ajoute simplement un élément de ligne à la liste. La structure de données interne pour les données traitées internes peut être une liste liée ou un tableau qui peut augmenter en taille.

L’adaptateur de sortie est un module qui accède à la liste des éléments de ligne, détermine si un élément de ligne traverse le rayon vers le haut (nombre 1) ou non (nombre 0). La somme de tous ces nombres donne un nombre total. L’adaptateur de sortie génère finalement une réponse « oui » (in-gamut) ou « non » (hors gamut), selon que le nombre total est impair ou pair. L’étape où vous déterminez si un élément de ligne traverse le rayon vers le haut mérite une certaine attention, car c’est là que se pose le problème de la dégénération et aussi le problème du surcomptent. Après [O’Rourke], pour qu’un élément de ligne traverse le rayon, le point d’extrémité droit (point d’extrémité avec une chromaie plus grande) doit être strictement sur le côté droit du rayon. Cela garantit que, si un point de terminaison se trouve exactement sur le rayon, il n’est compté qu’une seule fois. La même règle résout également la situation dégénérée où l’élément de ligne se trouve exactement sur le rayon. Vous n’incrémentez pas le nombre pour cet élément de ligne.

La figure 30 montre les éléments de ligne résultants d’un exemple de gamut avec le point de requête dans différentes positions.

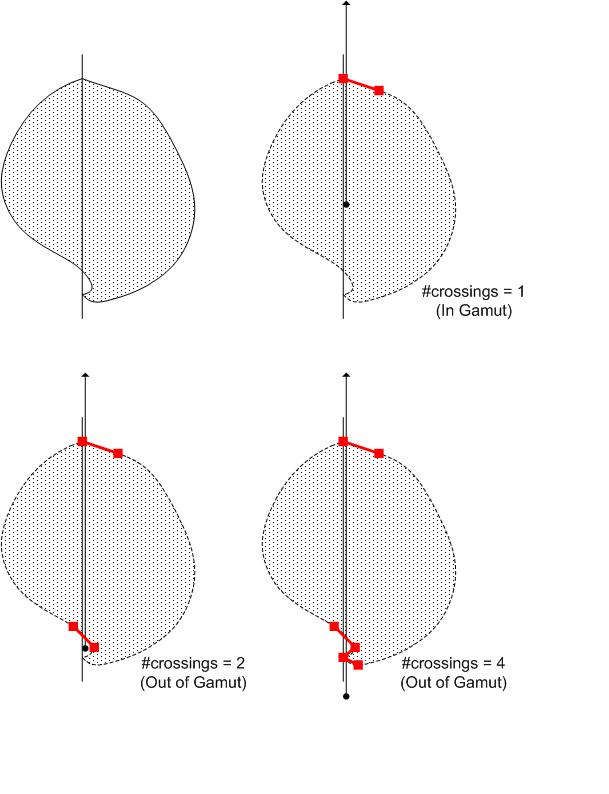
Figure 30 : Fonctionnement de CheckGamut

Mappage de la gamut de différence de couleur minimale

Le mappage minimum de la différence de couleur gamut, MinDEMap, a une spécification simple : si une couleur est in-gamut, ne rien faire. Si une couleur est hors gamut, projetez-la sur le point « le plus proche » de la limite de gamut. La mot clé « la plus proche » n’est pas bien définie tant que vous n’avez pas spécifié l’équation de différence de couleur à utiliser. Dans la pratique, pour faciliter et accélérer le calcul, la distance euclidienne de l’espace d’apparence de couleur choisi, ou une variante de celui-ci, est utilisée comme métrique de différence de couleur. L’avantage de la métrique euclidienne est qu’elle est compatible avec le produit point de l’espace, ce qui permet d’utiliser l’algèbre linéaire. En détail, si un « produit point » est défini dans l’espace, une distance peut être définie comme racine carrée du produit point du vecteur de différence avec lui-même. Un produit à points peut généralement être défini par une matrice A 3x3 définie positive.

u?v = u _T Av

où le côté droit est la multiplication de matrice habituelle. Si A est la matrice d’identité, le produit à points standard est récupéré. Dans la pratique, si Jab est l’espace de couleurs, vous ne souhaitez pas mélanger les composants. Une matrice diagonale autre que la matrice d’identité peut donc être utilisée. En outre, vous pouvez conserver l’échelle sur un et b inchangé afin que la mesure de teinte soit conservée. Par conséquent, une variante utile du produit à points euclidien standard est la suivante.

w _J (composant J de vous)(composant J de v) + (un composant de vous)(un composant de v) + (b composant de vous)(b composant de v)

où w _J est un nombre positif. Une autre variante consiste à laisser w _J varier avec le point de requête d’entrée :

w _{J\ =} w _J (queryPoint)

Le résultat final est une mesure de la distance asymétrique par rapport aux deux points, et avec des pondérations relatives différentes sur la légèreté et la chroma ou la teinte à mesure que le point de requête d’entrée varie. Cela est conforme à certaines observations sur la perception des couleurs humaines selon laquelle les différences de couleur ne sont pas pondérées de façon égale dans toutes les dimensions. Il a été constaté que les gens sont moins sensibles aux différences de légèreté qu’aux différences de teinte et de chroma.

La fonction de pondération suivante est utile.

w _J = k ₂ - k ₁ (C - C mₐₓ ) n

où k = 1, k ₁ = 0,75/(C mₐₓ ) n, C mₐₓ = 100, n = 2 et C est le plus petit de la chroma du point de requête et C mₐₓ.

de sorte qu’un poids de 0,25 est placé sur le terme J lorsque la chroma est égale à zéro, et un poids de 1 lorsque la couleur est 100. La tendance à mettre moins de poids sur J lorsque la chroma est petite, et plus de poids sur J lorsque la couleur est grande suit l’utilisation recommandée pour CMC et CIEDE2000.

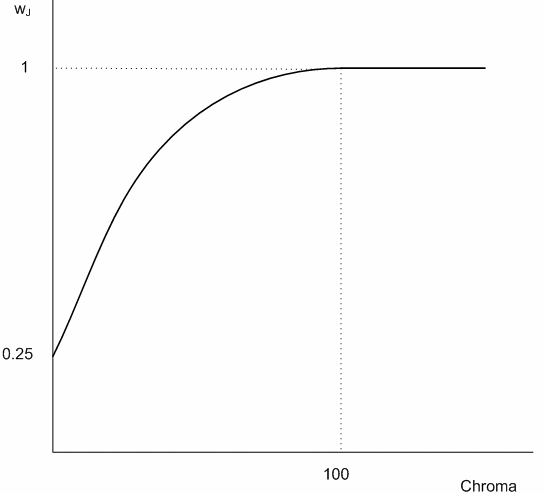
Figure 31 : Fonction de pondération sur le composant J de la métrique

Utilisez l’espace Jab pour l’exemple suivant. Il est difficile d’effectuer une recherche dans tous les triangles de limite pour déterminer le point le plus proche de la métrique euclidienne. Il s’agit d’une approche simple pour rendre ce processus aussi efficace que possible, sans introduire d’hypothèses supplémentaires qui peuvent accélérer le processus, mais aussi aboutir à une réponse approximative. Tout d’abord, il est nécessaire de comprendre la procédure géométrique de projection d’un point sur le triangle donné. Une description est donnée ici.

Une projection orthogonale sur le plan infini contenant le triangle est d’abord effectuée. La distance la plus courte du point de requête par rapport au plan peut être déterminée en deux étapes.

(a) Calculez l’unité vecteur normal du triangle.

(b) Calculer le produit de point du vecteur normal unitaire et un vecteur formé à partir du point de requête et d’un point sur le triangle; c’est-à-dire un de ses sommets. Étant donné que le vecteur normal a une longueur d’unité, la valeur absolue de ce produit point est la distance du point de requête par rapport au plan.

Le point projeté peut ne pas être la réponse, car il peut se trouver en dehors du triangle. Vous devez donc d’abord effectuer une case activée. Le calcul équivaut à calculer les coordonnées barycentriques du point projeté par rapport au triangle. Si le point projeté est déterminé comme étant à l’intérieur du triangle, il s’agit de la réponse. Si ce n’est pas le cas, le point le plus proche est acquis sur l’un des bords du triangle. Effectuez une recherche sur chacun des trois bords. La détermination de la projection du point de requête sur un bord est un processus similaire à la projection sur le triangle, mais une dimension en moins. Une projection orthogonale est d’abord calculée. Si le point projeté se trouve sur le bord, il s’agit de la réponse. Si ce n’est pas le cas, le point le plus proche est acquis sur l’un des deux points de terminaison. Effectuer une recherche sur les deux points de terminaison ; autrement dit, calculez la distance du point de requête par rapport à chacun d’eux et comparez celui qui est plus petit.

Un examen attentif révèle qu’il y a beaucoup de recherches répétées lorsque vous passez par tous les triangles, car un bord est toujours partagé par deux triangles et un sommet partagé par au moins trois bords. En outre, vous n’êtes pas très intéressé à trouver le point le plus proche d’un triangle particulier; au lieu de cela, vous souhaitez trouver le point le plus proche de la limite de la gamme entière. Toutefois, un triangle particulier serait celui dans lequel cela est réalisé. Vous pouvez utiliser deux stratégies pour accélérer la recherche.

Stratégie I. Chaque sommet sera traité, au maximum, une fois. Chaque arête sera traitée, au maximum, une fois.

Stratégie II. À tout moment dans la recherche, vous avez un meilleur candidat avec la meilleure distance correspondante. Si vous pouvez déterminer, par un case activée rapide, qu’un triangle n’est pas capable de donner une meilleure distance, il n’est pas nécessaire de poursuivre le calcul. Vous n’avez pas besoin du point et de la distance les plus proches pour ce triangle.

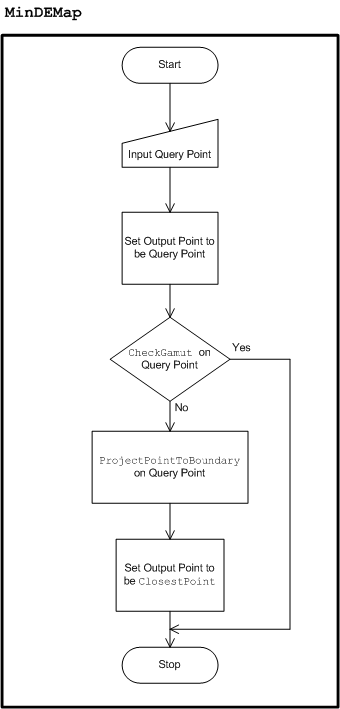
Figure 32 : Schémas de mappage DE minimum

La figure 32 montre le flux général de logique pour la carte de gamut MinDEMap. Pour un point de requête, la fonction CheckGamut est d’abord appelée. Si le point est in-gamut, la carte est un no-op. Si le point est hors gamme, appelez ProjectPointToBoundary. Passez maintenant à la figure 33. À ce stade, il est supposé que les valeurs suivantes ont été calculées.

(a) Unité du vecteur normal à chaque triangle de limite de gamut par rapport au produit à points standard.

(b) Liste de vertex et liste d’arêtes, en plus de la liste de triangles.

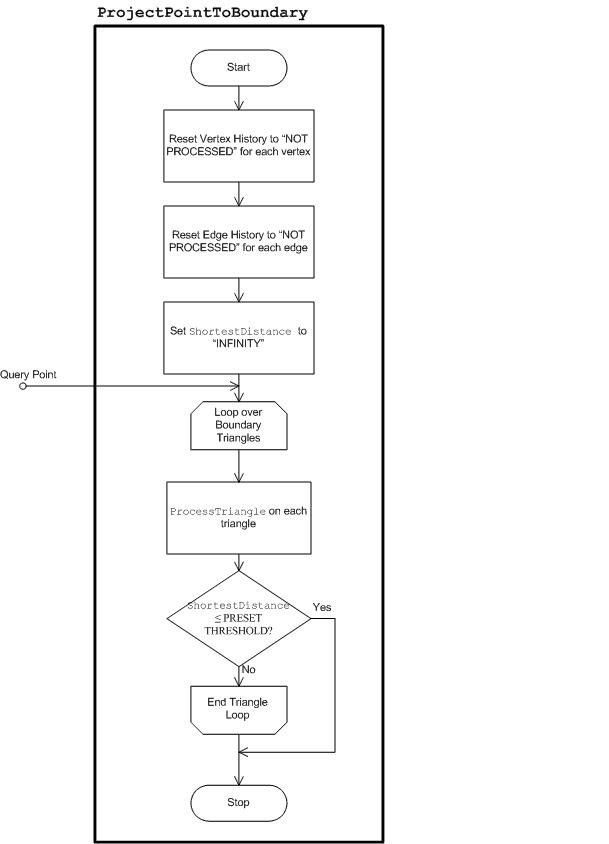
Figure 33 : Routine ProjectPointToBoundary

Toutes ces opérations représentent une surcharge constante et auraient un coût décroissant si suffisamment de requêtes à cette limite de gamme sont effectuées. En règle générale, c’est le cas lorsque vous générez un LUT de transformation d’un appareil à un autre, où il n’y a que deux gammes fixes, et où le LUT de transformation s’exécute à travers des points sur la grille échantillonné uniformément. Vous calculez au préalable les vecteurs normaux par rapport au produit dot standard, même si la notion de perpendicularité sera basée sur le produit de points pondéré, qui dépend du point de requête comme expliqué précédemment. La raison en est qu’un vecteur normal par rapport au produit à points pondéré peut être obtenu facilement à partir du vecteur normal par rapport au produit à points standard. Si n ₀ est un vecteur normal par rapport au produit de point standard, alors

n = (J-component of n ₀ /w _J, a-component of n ₀, b-component of n ₀ )

est normal au triangle par rapport au produit à points pondéré. En raison de cette relation, il est toujours avantageux de précalcaliser n ₀ même s’il doit être ajusté en fonction du point de requête.

La routine ProjectPointToBoundary commence par réinitialiser l'« historique traité » des sommets et des arêtes. Il s’agit de tables d’indicateurs BOOLEAN qui indiquent si un sommet ou un bord a déjà été visité. Il réinitialise également la variable ShortestDistance à « INFINITY », qui est la valeur maximale encodée dans le système de nombre à virgule flottante utilisé. Ensuite, il s’exécute à travers une boucle, recherchant le point le plus proche de chaque triangle à l’aide de l’appel ProcessTriangle. ProcessTriangle est la routine permettant de mettre à jour la variable ShortestDistance et se trouve clairement dans la boucle critique. Une optimisation consiste à s’arrêter lorsque le résultat est suffisamment bon. Après chaque appel à ProcessTriangle, la variable ShortestDistance est examinée. S’il satisfait à un seuil prédéfini, vous pouvez arrêter. Le seuil prédéfini dépend de l’espace de couleurs utilisé et de la précision requise du système d’imagerie des couleurs. Pour une application classique, vous ne souhaitez pas effectuer de travail inutile si la différence de couleur est inférieure à ce qui peut être discerné par la vision humaine. Pour CIECAM02, cette différence de couleur est 1. Utilisez toutefois une valeur de seuil de 0,005 dans l’implémentation pour conserver la précision des calculs, car il peut ne s’agir que d’une étape intermédiaire dans une chaîne de transformations.

ProcessTriangle implémente la stratégie PRÉCÉDENTE. En obtenant un vecteur normal du vecteur normal d’unité précalpliquée vers le triangle par rapport au produit de point standard, il calcule la distance du point de requête au plan infini contenant le triangle en formant le produit de point du vecteur normal d’unité et le queryVector, le vecteur de l’un des sommets du triangle, vertex1, au point de requête, queryPoint.

queryVector = queryPoint - vertex1

distance = | normalVector * queryVector |/|| normalVector||

Il s’agit d’un calcul relativement peu coûteux, et la distance est nécessaire pour effectuer d’autres calculs. Si cette distance n’est pas inférieure à la meilleure distance actuelle, ShortestDistance, ce triangle ne produira pas une meilleure distance, car il ne donnera pas une meilleure distance que le plan qui le contient. Dans ce cas, vous retournez le contrôle à la boucle triangle. Si la distance est inférieure à ShortestDistance, vous avez potentiellement un point plus proche, si ce point se trouve à l’intérieur du triangle. Vous devez effectuer des calculs « durs » (mais rien au-delà de l’algèbre linéaire) pour le déterminer. Si les deux autres sommets du triangle sont vertex2 et vertex3, formez les vecteurs de base d’abordBasisVector et secondBasisVector.

firstBasisVector = vertex2 - vertex1

secondBasisVector = vertex3 - vertex1

Utilisez le système linéaire d’équations suivant pour résoudre les inconnues vous et v.

firstBasisVector * queryVector = (firstBasisVector * firstBasisVector)u + (firstBasisVector * secondBasisVector)v

secondBasisVector * queryVector = (secondBasisVector * firstBasisVector)u + (secondBasisVector * secondBasisVector)v

et les conditions pour que le point projeté se trouve à l’intérieur du triangle sont les suivantes :

0 ≤ u ≤ 1, 0 ≤ v ≤ 1 et vous + v ≤ 1

Après ce calcul, s’il est déterminé que le point projeté se trouve dans le triangle, vous avez trouvé un nouveau point le plus proche; la distance que vous avez calculée au début est la nouvelle distance la plus courte. Dans ce cas, mettez à jour les variables ShortestDistance et ClosestPoint. Si le point projeté se trouve à l’extérieur du triangle, vous pouvez trouver un point plus proche sur l’un de ses bords. Vous pouvez donc appeler la routine ProcessEdge sur chacun des trois bords.

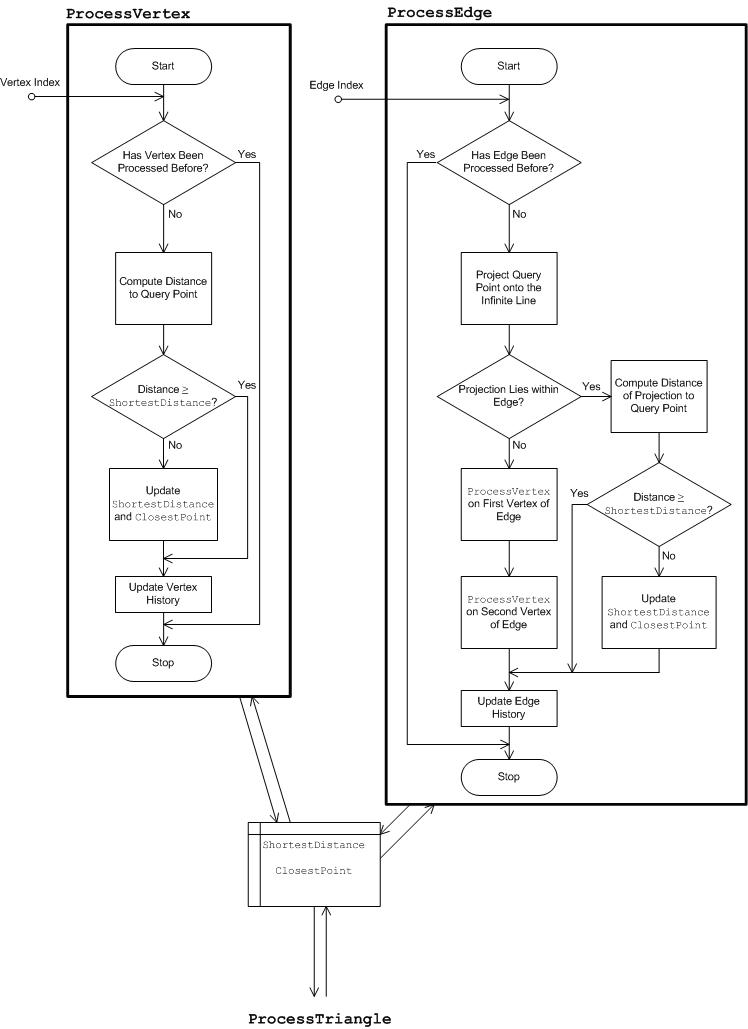
Figure 34 : Routines ProcessEdge et ProcessVertex

La routine ProcessEdge implémente la stratégie I, illustrée à la figure 34. ProcessEdge commence par vérifier si l’arête a déjà été traitée. Si c’est le cas, aucune autre mesure n’est prise. Si ce n’est pas le cas, il calcule la projection orthogonale du point de requête sur la ligne infinie contenant le bord. L’algèbre linéaire impliquée dans le calcul est similaire aux équations de triangle précédentes. Toutefois, le calcul est plus simple, il n’est pas décrit ici. Si le point projeté se trouve dans le bord, vous trouvez la distance entre le point projeté et le point de requête. Si cette distance est inférieure à ShortestDistance, vous avez trouvé un nouveau point le plus proche. Mettez à jour ShortestDistance et ClosestPoint. Si le point projeté se trouve en dehors du bord, appelez ProcessVertex sur les deux points de terminaison. Avant de retourner le contrôle, mettez à jour l’historique des arêtes afin que ce bord soit marqué comme « TRAITÉ ».

Enfin, vous fournissez une description de ProcessVertex. La routine ProjectVertex implémente également la stratégie I et gère une table d’historique des vertex. Comme illustré dans la figure 34, il vérifie d’abord si le vertex a été traité auparavant. Si c’est le cas, aucune autre mesure n’est prise. Si ce n’est pas le cas, il calcule la distance du sommet par rapport au point de requête. Si la distance est inférieure à ShortestDistance, mettez à jour ShortestDistance et ClosestPoint. À la fin, il met à jour l’historique des vertex afin que ce sommet soit marqué comme « TRAITÉ ».

Lorsque la boucle de contrôle externe a épuisé tous les triangles ou s’est terminée avant que le seuil de différence de couleur n’ait été atteint, la variable ClosestPoint est accessible. Il s’agit du résultat de MinDEMap. L’appelant peut également récupérer ShortestDistance s’il est intéressé par la distance entre la couleur mappée et la couleur de requête.

Lissage des teintes

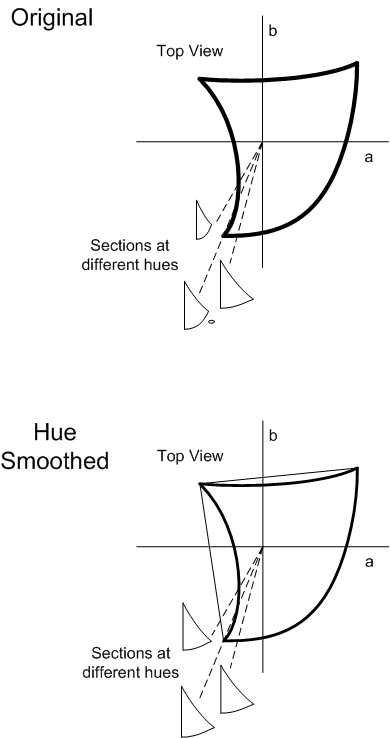
Figure 35 : Lissage des teintes

Un problème se produit avec les opérations qui sont limitées par la teinte ; autrement dit, l’opération prend uniquement en compte les variables au sein d’un plan de teinte. La figure 35 montre un exemple de gamme présentant des tranches de teinte « discontinues » dans les teintes bleues. Dans cette plage de teintes, pour certains angles de teinte, la limite de la gamme est tangentielle au plan de teinte. En effet, cela entraîne une modification de la structure topologique des tranches de teinte. Dans l’exemple illustré, à mesure que le plan de teinte balaye cette plage de teintes, une « île » émerge et submerge. Cette modification de la topologie entraîne la discontinuité des opérations spécifiques à la teinte. Par exemple, le cusp à teinte fixe change brusquement à mesure que l’angle de teinte change dans cette plage.

Il existe une raison de la science des couleurs pour laquelle il est souhaitable de conserver la teinte dans certaines opérations. Pour résoudre le problème précédent, les triangles de limites de gamut d’origine doivent être « lissés de teinte ». En règle générale, un lissage de teinte d’un ensemble de triangles de limites de gamut est un ensemble de triangles de telle sorte que (a) il forme la limite d’un nouveau « gamut », qui peut ne pas correspondre au gamut réel de l’appareil et qui contient la gamme définie par l’ensemble de triangles d’origine ; et (b) les triangles du nouvel ensemble ne sont pas parallèles aux plans de teinte.

Une façon pratique d’obtenir une teinte lissée ensemble de triangles est de prendre la coque convexe des sommets d’origine. Comme l’illustre la figure 35, les tranches de teinte de la coque convexe varient en douceur dans la plage de teintes problématique sans changer soudainement la topologie.

Définition des valeurs primaires et secondaires dans la description de la limite de gamut

Certaines méthodes de mappage de gamut, telles que HueMap, dépendent de l’emplacement des primaires et des secondaires des appareils. Pour les appareils additifs, les primaires sont rouges, vertes et bleues (R, G et B); et les secondaires sont cyan, magenta et jaune (C, M et Y). Pour les appareils soustractifs, les primaires sont C, M et Y; et les secondaires sont R, G et B. Le GBD effectue le suivi de ces six valeurs, ainsi que le blanc et le noir (W et K), dans un tableau de valeurs de couleur Jab. Ces valeurs sont définies dans la description de la limite de gamut lors de sa création. Pour les appareils de sortie, les valeurs primaires peuvent être déterminées en exécutant des combinaisons de valeurs de contrôle d’appareil via le modèle d’appareil. Pour les appareils de capture, cette approche n’est pas bien adaptée à la création du GBD de référence, car il est presque impossible de capturer une image qui produit une valeur d’appareil pur entièrement saturée, telle que (0.0, 0.0, 1.0). Les profils d’appareil WCS contiennent les index des primaires dans la cible de capture. Étant donné que ces valeurs ne sont pas contenues dans un profil ICC, utilisez des valeurs mesurées à partir d’une cible de scanneur classique après la conversion en Jab, par rapport aux conditions d’affichage ICC.

Définition de l’axe neutre dans la description de la limite de gamut

Les méthodes de mappage de la gamme HueMap et Relative MinCD utilisent l’axe neutre de l’appareil pour le redressement. Pour les périphériques de sortie de base, l’axe neutre peut être déterminé en exécutant des valeurs neutres d’appareil (R=G=B ou C=M=Y) via la méthode DeviceToColorimetric, puis via la méthode ColorimetricToAppearance de l’objet CIECAM02. Toutefois, les appareils de capture ne retournent pas toujours une valeur neutre d’appareil lorsqu’ils sont présentés avec un échantillon neutre. Cela est particulièrement vrai lorsque l’éclairage ambiant n’est pas parfaitement neutre. Les profils d’appareil WCS contiennent les index des échantillons neutres dans la cible. Utilisez ces exemples pour définir l’axe neutre. Étant donné que ces informations ne sont pas disponibles pour les profils ICC, vous devez utiliser la même méthode que celle utilisée pour les périphériques de sortie ; exécutez des exemples de périphérique neutres via la méthode DeviceToColorimetric, puis couplez les valeurs d’entrée et les résultats colorimétriques.

Rubriques connexes

Concepts de base de la gestion des couleurs

Schémas et algorithmes du système de couleurs Windows