Rotation, réflexion et rotation des images

Vous pouvez faire pivoter, refléter et faire pivoter une image en spécifiant des points de destination pour les coins supérieur gauche, supérieur droit et inférieur gauche de l’image d’origine. Les trois points de destination déterminent une transformation affine qui mappe l’image rectangulaire d’origine à un paralléliogramme. (Le coin inférieur droit de l’image d’origine est mappé au quatrième coin du paralléliogramme, qui est calculé à partir des trois points de destination spécifiés.)

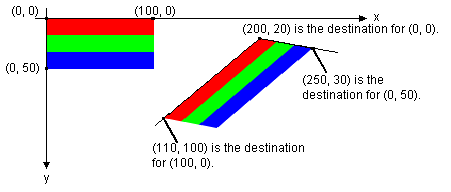
Par exemple, supposons que l’image d’origine soit un rectangle avec un coin supérieur gauche à (0, 0), un coin supérieur droit à (100, 0) et un coin inférieur gauche à (0, 50). Supposons maintenant que nous mapper ces trois points aux points de destination comme suit.

Point d’origine	Point de destination
En haut à gauche (0, 0)	(200, 20)
Haut à droite (100, 0)	(110, 100)
En bas à gauche (0, 50)	(250, 30)

 

L’illustration suivante montre l’image d’origine et l’image mappée au paralléliogramme. L’image d’origine a été décalé, réfléchie, pivotée et traduite. L’axe X le long du bord supérieur de l’image d’origine est mappé à la ligne qui traverse (200, 20) et (110, 100). L’axe y le long du bord gauche de l’image d’origine est mappé à la ligne qui traverse (200, 20) et (250, 30).

L’exemple suivant produit les images présentées dans l’illustration précédente.

Point destinationPoints[] = {
   Point(200, 20),   // destination for upper-left point of original
   Point(110, 100),  // destination for upper-right point of original
   Point(250, 30)};  // destination for lower-left point of original
Image image(L"Stripes.bmp");
// Draw the image unaltered with its upper-left corner at (0, 0).
graphics.DrawImage(&image, 0, 0);
// Draw the image mapped to the parallelogram.
graphics.DrawImage(&image, destinationPoints, 3); 

L’illustration suivante montre une transformation similaire appliquée à une image photographique.

L’illustration suivante montre une transformation similaire appliquée à un métafichier.