Courbes de paramètres
Les paramètres multimédias peuvent suivre une courbe au fil du temps. Chaque courbe est décrite par une formule mathématique et deux points de terminaison. Chaque point de terminaison est défini par une heure de référence et la valeur de la courbe à ce moment-là. La formule est utilisée pour calculer des valeurs intermédiaires entre les points et détermine la forme de la courbe. Les courbes possibles sont les suivantes :
- Sauter
- Linéaire
- Carré
- Carré inverse
- Sinus
« Sauter » signifie passer directement à la valeur de fin. Les autres courbes sont illustrées dans le diagramme suivant.
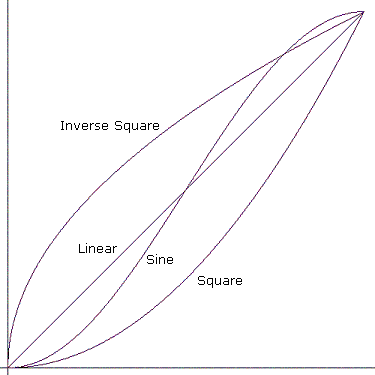
Mathématiquement, les courbes fonctionnent comme suit. Supposons qu’une courbe commence à l’heure t₀ avec une valeur de v₀ et se termine à l’heure t₁ avec la valeur v₁. Les deux points qui définissent la courbe sont (t₀, v₀) et (t₁, v₁).
- Soit Δt la durée totale de la courbe, t₁–t₀.
- Δv est l’intervalle entre les valeurs de début et de fin, v₁–v₀.
- À tout moment t tel que t₀ <= t<= t₁, let Δt'= t–t₀.
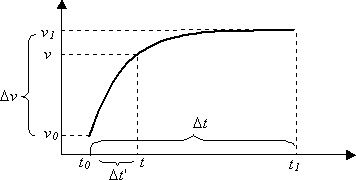
La valeur du paramètre à l’heure t est la suivante :
v = f( Δt'/ Δt ) * Δv + v₀
où f(x) est une fonction déterminée par le type de courbe :
- Linéaire : y = x
- Carré : y = x^2
- Carré inverse : y = sqrt(x)
- Sinus : y = [ sin(πx – π/2) + 1 ] / 2
Notez que Δt’Δ<t, le terme Δt'/Δt est donc de 0 à 1. Par conséquent, f(x) est également compris entre 0 et 1, et v se situe toujours entre v₀ et v₁. Cela est vrai que v₀ <v₁ ou vice versa. En d’autres termes, la courbe est limitée par le rectangle (t₀, v₀, t₁, v₁).
Pour la courbe sinusoïdale, la valeur de (πx – π/2) est comprise entre –π/2 et π/2, ce qui signifie que sin(πx – π/2) est comprise entre –1 et 1. Le résultat est ensuite normalisé de sorte que f(x) tombe dans la plage (0 à 1).
Rubriques connexes