Transfert de radiance précalculé (Direct3D 9)

Utilisation du transfert de radiance précalculé

Il existe plusieurs formes de complexité présentes dans des scènes intéressantes, notamment la façon dont l’environnement d’éclairage est modélisé (c’est-à-dire les modèles d’éclairage de zone par rapport aux modèles point/directionnels) et le type d’effets globaux qui sont modélisés (par exemple, ombres, interreflections, diffusion en sous-surface). Les techniques de rendu interactives traditionnelles modélisent une quantité limitée de cette complexité. Le PRT permet ces effets avec des restrictions importantes :

• Les objets sont supposés être rigides (c’est-à-dire aucune déformation).
• Il s’agit d’une approche centrée sur les objets (à moins que les objets ne soient déplacés ensemble, ces effets globaux ne sont pas conservés entre eux).
• Seul l’éclairage basse fréquence est modélisé (ce qui entraîne des ombres douces).) Pour les lumières à haute fréquence (ombres vives), il faudrait utiliser des techniques traditionnelles.

PRT nécessite l’une des opérations suivantes, mais pas les deux :

• modèles et vs_1_1 à haute tessellation
• ps_2_0

Éclairage diffus standard et PRT

L’illustration suivante est rendue à l’aide du modèle d’éclairage traditionnel (n · l). Les ombres nettes peuvent être activées à l’aide d’une autre passe et d’une certaine forme de technique de ombrage (cartes de profondeur d’ombre ou volumes d’ombres). L’ajout de plusieurs lumières nécessiterait plusieurs passes (si des ombres doivent être utilisées) ou des nuanceurs plus complexes avec des techniques traditionnelles.

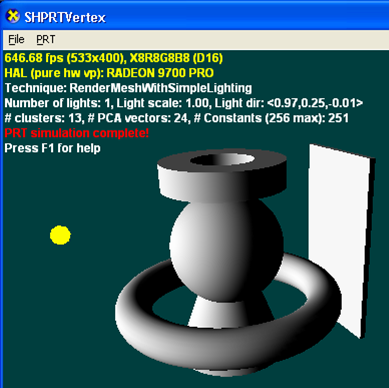
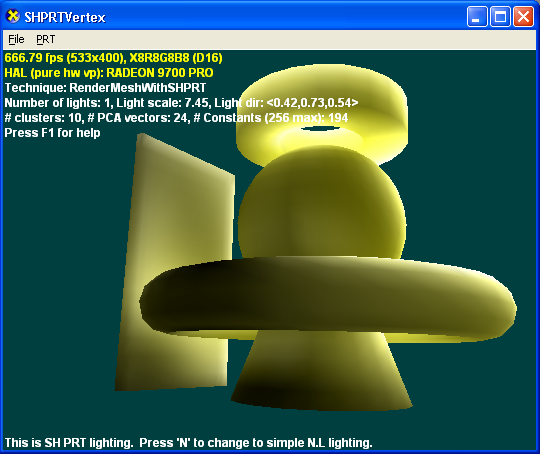
L’illustration suivante est rendue avec PRT à l’aide de la meilleure approximation d’une seule lumière directionnelle qu’elle peut résoudre. Il en résulte des ombres douces qui seraient difficiles à produire avec des techniques traditionnelles. Étant donné que PRT modélise toujours des environnements d’éclairage complets en ajoutant plusieurs lumières ou en utilisant une carte d’environnement, vous ne modifieriez que les valeurs (mais pas le nombre) de constantes utilisées par le nuanceur.

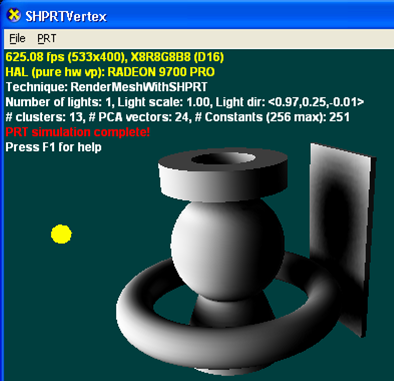
PRT avec interreflections

L’éclairage direct atteint la surface directement à partir de la lumière. Les interreflections sont des lumières qui atteignent la surface après avoir rebondit sur une autre surface un certain nombre de fois. PRT peut modéliser ce comportement sans modifier les performances au moment de l’exécution en exécutant simplement le simulateur avec des paramètres différents.

L’illustration suivante est créée à l’aide de PRT direct uniquement (0 rebonds sans interréférences).

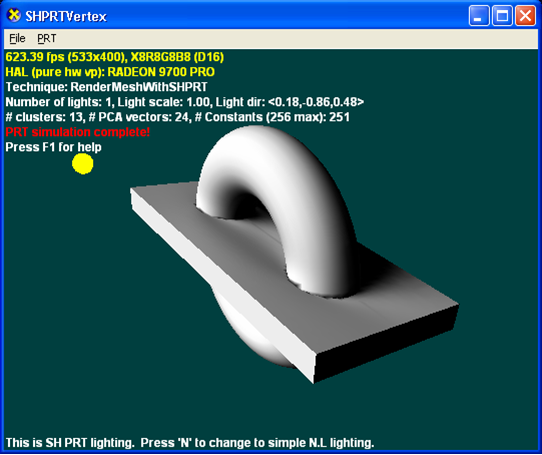
L’illustration suivante est créée à l’aide de PRT avec des interreflections (2 rebonds avec des interreflections).

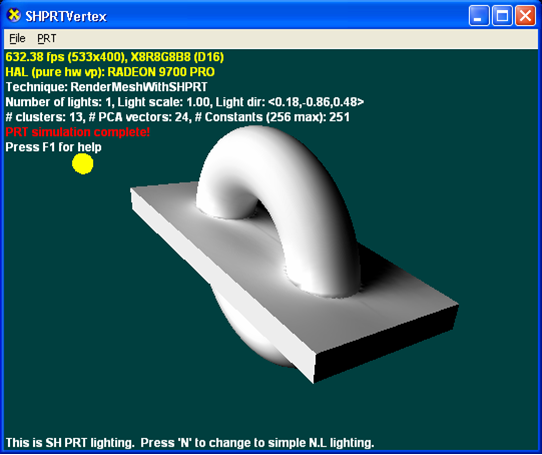
PRT avec nuage de points subsurface

La diffusion subsurface est une technique qui modélise la façon dont la lumière passe à travers certains matériaux. Par exemple, appuyez sur une lampe de poche allumée contre la paume de votre main. La lumière de la lampe de poche passe par votre main, rebondit (changement de couleur dans le processus) et sort de l’autre côté de votre main. Cela peut également être modélisé avec des modifications simples apportées au simulateur et aucune modification du runtime.

L’illustration suivante illustre le PRT avec la diffusion en sous-surface.

Fonctionnement du PRT

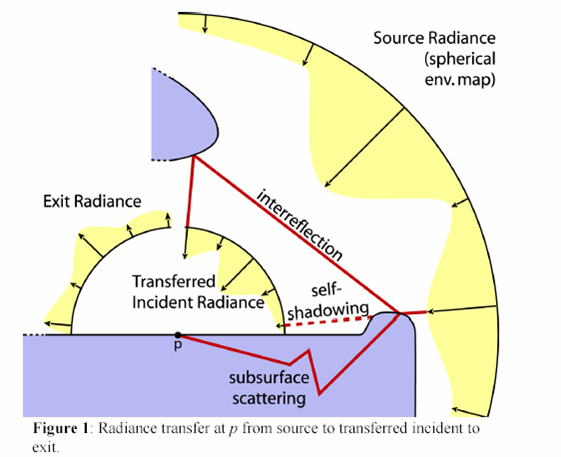
Les termes suivants sont utiles pour comprendre le fonctionnement du PRT, comme illustré dans le diagramme suivant.

Source Radiance : Le rayonnement source représente l’environnement d’éclairage dans son ensemble. En PRT, un environnement arbitraire est approximatif à l’aide de la base harmonique sphérique - cet éclairage est supposé être distant par rapport à l’objet (la même hypothèse que celle qui est faite avec les cartes d’environnement.)

Radiance de sortie : l’éclat de sortie est la lumière sortant d’un point sur la surface à partir de n’importe quelle source possible (rayonnement réfléchi, diffusion en sous-surface, émission).

Vecteurs de transfert : les vecteurs de transfert mappent source radiance dans le rayonnement de sortie et sont précalculés hors connexion à l’aide d’une simulation de transport de lumière complexe.

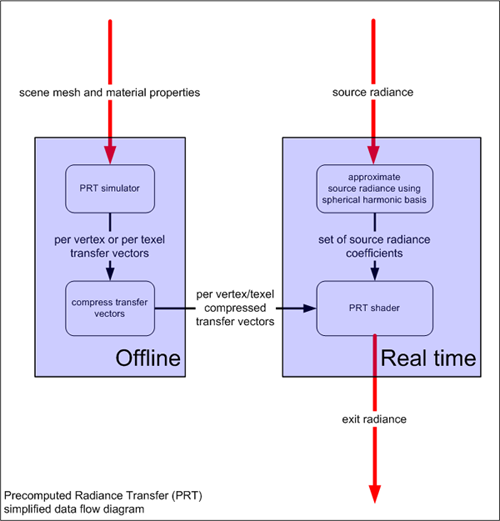
PrT détermine le processus de rendu en deux étapes, comme illustré dans le diagramme suivant :

1. Une simulation de transport léger coûteuse précalcule des coefficients de transfert qui peuvent être utilisés au moment de l’exécution.
2. Une étape d’exécution relativement légère se rapproche d’abord de l’environnement d’éclairage à l’aide de la base harmonique sphérique, puis utilise ces coefficients d’éclairage et les coefficients de transfert précalculés (à partir de l’étape 1) avec un nuanceur simple, ce qui donne un éclat de sortie (la lumière quittant l’objet).

Comment utiliser l’API PRT

1. Calculez les vecteurs de transfert avec l’un des calculs... méthodes de ID3DXPRTEngine.

   Le traitement direct de ces vecteurs de transfert nécessite une quantité importante de calcul de mémoire et de nuanceur. La compression réduit considérablement la quantité de mémoire et le calcul du nuanceur requis.

   Les valeurs d’éclairage finales sont calculées dans un nuanceur de vertex qui implémente l’équation de rendu compressée suivante.

   

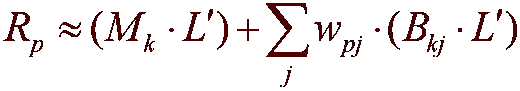
   Où :

   Paramètre	Description
   Rp	Un seul canal de rayonnement de sortie au sommet p et est évalué à chaque sommet du maillage.
   Mk	Moyenne du cluster k. Il s’agit d’un vecteur Order² de coefficients.
   k	ID de cluster pour vertex p.
   L'	Approximation du rayonnement source dans les fonctions de base SH. Il s’agit d’un vecteur Order² de coefficients.
   j	Entier qui est supérieur au nombre de vecteurs PCA.
   wpj	Poids jth PCA pour point p. Il s’agit d’un coefficient unique.
   Bkj	Vecteur de base jth PCA pour le cluster k. Il s’agit d’un vecteur Order² de coefficients.

    

   Extraire... les méthodes d’ID3DXPRTCompBuffer permettent d’accéder aux données compressées à partir de la simulation.

2. Calculez le rayonnement source.

   Il existe plusieurs fonctions d’assistance dans l’API pour gérer divers scénarios d’éclairage courants.

   Fonction	Objectif
   D3DXSHEvalDirectionalLight	Se rapproche d’une lumière directionnelle conventionnelle.
   D3DXSHEvalSphericalLight	Se rapproche des sources de lumière sphérique locales. (Notez que PRT fonctionne uniquement avec les environnements d’éclairage à distance.)
   D3DXSHEvalConeLight	Se rapproche d’une source de lumière de zone distante. Un exemple serait le soleil (très petit angle de cône).
   D3DXSHEvalHemisphereLight	Évalue une lumière qui est une interpolation linéaire entre deux couleurs (une sur chaque pôle d’une sphère).

    

3. Calculez le rayonnement de sortie.

   L’équation 1 doit maintenant être évaluée à chaque point à l’aide d’un nuanceur de vertex ou de pixels. Avant que le nuanceur puisse être évalué, les constantes doivent être précalculées et chargées dans la table de constantes (voir l’exemple de démonstration PRT pour plus d’informations). Le nuanceur lui-même est une implémentation simple de cette équation.

   struct VS_OUTPUT
   {
       float4 Position   : POSITION;   // vertex position 
       float2 TextureUV  : TEXCOORD0;  // vertex texture coordinates 
       float4 Diffuse    : COLOR0;     // vertex diffuse color
   };
   
   VS_OUTPUT Output;   
   Output.Position = mul(vPos, mWorldViewProjection);
   
   float4 vExitR = float4(0,0,0,0);
   float4 vExitG = float4(0,0,0,0);
   float4 vExitB = float4(0,0,0,0);
   
   for (int i=0; i < (NUM_PCA_VECTORS/4); i++) 
   {
      vExitR += vPCAWeights[i] * 
          vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*0];
      vExitG += vPCAWeights[i] * 
          vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*1];
      vExitB += vPCAWeights[i] * 
          vClusteredPCA[iClusterOffset+i+1+(NUM_PCA_VECTORS/4)*2];
   }
   
   float4 vExitRadiance = vClusteredPCA[iClusterOffset];
   vExitRadiance.r += dot(vExitR,1);
   vExitRadiance.g += dot(vExitG,1);
   vExitRadiance.b += dot(vExitB,1);
   
   Output.Diffuse = vExitRadiance;
   

Références

Pour plus d’informations sur le PRT et les harmoniques sphériques, consultez les articles suivants :

Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, 
Low-Frequency Lighting Environments 
P.-P. Sloan, J. Kautz, J. Snyder
SIGGRAPH 2002 

Clustered Principal Components for Precomputed Radiance Transfer 
P.-P. Sloan, J. Hall, J. Hart, J. Snyder 
SIGGRAPH 2003 

Efficient Evaluation of Irradiance Environment Maps 
P.-P. Sloan 
ShaderX 2,  W. Engel 

Spherical Harmonic Lighting: The Gritty Details 
R. Green 
GDC 2003 

An Efficient Representation for Irradiance Environment Maps 
R. Ramamoorthi, P. Hanrahan 

A Practical Model for Subsurface Light Transport 
H. W. Jensen, S. R. Marschner, M. Levoy, and P. Hanrahan 
SIGGRAPH 2001 

Bi-Scale Radiance Transfer 
P.-P. Sloan, X. Liu, H.-Y. Shum, J. Snyder
SIGGRAPH 2003 

Fast, Arbitrary BRDF Shading for Low-Frequency Lighting Using Spherical 
Harmonics 
J. Kautz, P.-P. Sloan, J. Snyder
12th Eurographics Workshop on Rendering 

Precomputing Interactive Dynamic Deformable Scenes 
D. James, K. Fatahalian 
SIGGRAPH 2003 

All-Frequency Shadows Using Non-linear Wavelet Lighting Approximation 
R. Ng, R. Ramamoorth, P. Hanrahan 
SIGGRAPH 2003 

Matrix Radiance Transfer 
J. Lehtinen, J. Kautz
SIGGRAPH 2003 

Math World 
E. W. Weisstein, Wolfram Research, Inc. 

Quantum Theory of Angular Momentum 
D. A. Varshalovich, A.N. Moskalev, V.K. Khersonskii 

Rubriques connexes

Rubriques avancées

Équations PRT (Direct3D 9)

Représentation de PRT avec des textures (Direct3D 9)

ID3DXPRTBuffer

ID3DXPRTCompBuffer

ID3DXPRTEngine

ID3DXTextureGutterHelper

Fonctions de transfert de radiance précalculées

Fonctions mathématiques