Régression linéaire multiple et R-carré

Effectué

Dans cette unité, nous opposerons la régression linéaire multiple à la régression linéaire simple. Nous examinerons également une métrique appelée R², qui est couramment utilisée pour évaluer la qualité d'un modèle de régression linéaire.

Régression linéaire multiple

La régression linéaire multiple modélise la relation entre plusieurs caractéristiques et une seule variable. Mathématiquement, il n'y a pas de différence avec la régression linéaire simple, et elle est généralement ajustée à l'aide de la même fonction de coût, mais avec plus de caractéristiques.

Au lieu de modéliser une seule relation, cette technique modélise simultanément plusieurs relations, qu’elle traite comme indépendantes les unes des autres. Par exemple, si nous prédisons l’état de santé d’un chien en fonction de age (âge) et de body_fat_percentage (indice de masse corporelle), deux relations sont trouvées :

• Comment l'âge accentue ou diminue les symptômes de la maladie
• Comment l'indice de masse corporelle accentue ou diminue les symptômes de la maladie

Si nous utilisons uniquement deux caractéristiques, nous pouvons visualiser notre modèle sous la forme d’un plan (une surface plane en 2D), tout comme nous pouvons modéliser une régression linéaire simple sous la forme d’une droite. C'est ce que nous allons étudier dans l'exercice suivant.

La régression linéaire multiple s'appuie sur des hypothèses

Le fait que le modèle s'attende à ce que les caractéristiques soient indépendantes est appelé une hypothèse de modèle. Quand les hypothèses du modèle se révèlent fausses, le modèle peut effectuer des prédictions trompeuses.

Par exemple, l’âge permet de prédire l’état de santé des chiens, dans la mesure où les chiens âgés sont de plus en plus malades. De même, il permet de prédire que les chiens ont appris à jouer au frisbee dans la mesure où les chiens âgés savent probablement tous jouer au frisbee. Si nous avions inclus age et knows_frisbee (sait jouer au frisbee) dans notre modèle en tant que caractéristiques, celui-ci nous indiquerait probablement que knows_frisbee est un bon prédicteur de maladie, et sous-estimerait l’importance de age. Cela est un peu absurde, car le fait de savoir jouer au frisbee ne rend pas malade. En revanche, dog_breed (race du chien) peut également être un bon prédicteur de maladie. Toutefois, dans la mesure où il n’existe aucune raison de croire que age permet de prédire dog_breed, il est plus prudent d’inclure ces deux caractéristiques dans un modèle.

Qualité de l'ajustement : R²

Nous savons que les fonctions de coût peuvent être utilisées pour évaluer l’ajustement d’un modèle par rapport aux données à partir desquelles il a été entraîné. Les modèles de régression linéaire disposent d’une mesure associée spéciale appelée R² (R-carré). Le R² est une valeur comprise entre 0 et 1 qui nous indique dans quelle mesure un modèle de régression linéaire convient aux données. Lorsque l'on parle de corrélations fortes, cela signifie généralement que la valeur R² est élevée.

Le R² utilise des calculs mathématiques non couverts dans ce cours, mais nous pouvons y penser de manière intuitive. Prenons l’exercice précédent, où nous avons examiné la relation entre age et core_temperature (température corporelle interne). Un R² de 1 signifie que le nombre d’années permet de prédire avec précision qui a eu une température élevée, et qui a eu une température basse. En revanche, 0 signifie qu’il n’existe tout simplement aucune relation entre les années et la température.

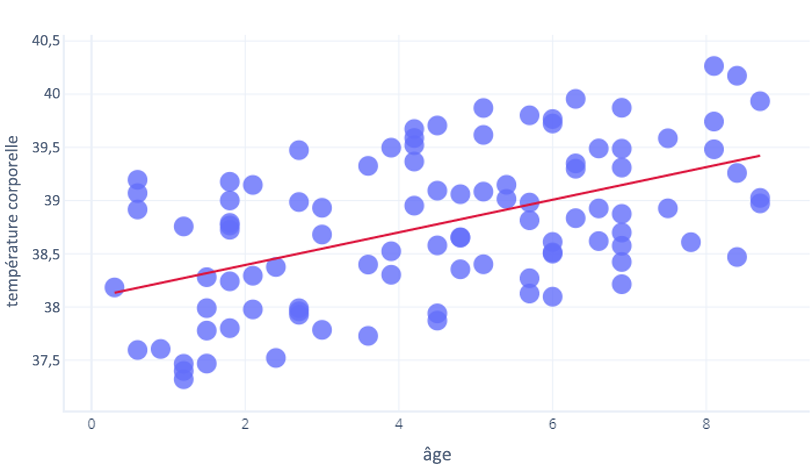
La réalité se situe entre les deux. Notre modèle peut prédire la température dans une certaine mesure (il est donc meilleur que R² = 0), mais les points ont quelque peu varié par rapport à cette prédiction (il est donc moins bon que R²=1).

R² n’indique pas tout.

Les valeurs R² sont largement acceptées, mais elles ne constituent pas une mesure parfaite que nous pouvons utiliser de manière isolée. Elles présentent quatre inconvénients :

• En raison de la façon dont le R² est calculé, plus nous avons d'échantillons, plus le R² est élevé. Cela peut nous amener à penser qu'un modèle est meilleur qu'un autre modèle (identique), simplement parce que les valeurs R² ont été calculées en utilisant des quantités différentes de données.
• Les valeurs R² ne nous permettent pas de savoir si un modèle fonctionnera avec des données nouvelles, inédites. Les statisticiens surmontent ce problème en calculant une mesure supplémentaire, appelée valeur p, que nous n’aborderons pas ici. Dans le cadre du Machine Learning, nous testons souvent explicitement notre modèle sur un autre jeu de données.
• Les valeurs R² ne nous indiquent pas la direction de la relation. Par exemple, une valeur R² de 0,8 ne nous indique pas si la droite est inclinée vers le haut ou vers le bas. Elle ne nous indique pas non plus le degré d'inclinaison de la droite.

Il convient également de garder à l’esprit qu’il n’existe aucun critère universel permettant de déterminer ce qui rend une valeur R² « assez bonne ». Par exemple, dans la plupart des domaines de la physique, les corrélations qui ne sont pas très proches de 1 sont peu susceptibles d’être considérées comme utiles. Toutefois, pour la modélisation de systèmes complexes, des valeurs R² aussi basses que 0,3 peuvent être considérées comme excellentes.