Qu’est-ce que la régression ?
La régression est une technique d’analyse des données simple, courante et très utile, souvent appelée familièrement « ajustement de ligne ». Dans sa forme la plus simple, la régression ajuste une ligne droite entre une variable (caractéristiques) et une autre variable (étiquette). Dans ses formes plus complexes, la régression peut trouver des relations non linéaires entre une étiquette et plusieurs caractéristiques.
Régression linéaire simple
La régression linéaire simple modélise une relation linéaire entre une caractéristique et une étiquette généralement continue, ce qui permet à la caractéristique de prédire l’étiquette. Visuellement, cela peut se présenter sous la forme suivante :
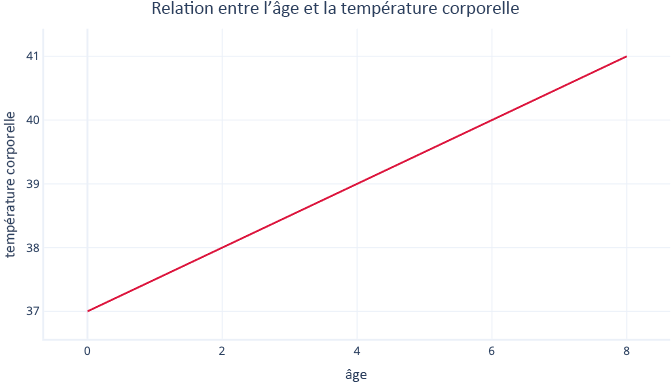
La régression linéaire simple a deux paramètres : un point d’intersection (c), qui indique la valeur de l’étiquette quand la caractéristique a la valeur zéro, et une pente (m), qui indique l’augmentation de l’étiquette pour chaque hausse d’un point de la caractéristique.
Mathématiquement, cela correspond à l'équation suivante :
y = mx + c
Sachant que y désigne votre étiquette, et x votre caractéristique.
Par exemple, dans notre scénario, si nous voulions essayer de prédire quels patients auront de la fièvre en fonction de leur âge, nous aurions le modèle suivant :
température = m * âge + c
Vous devez trouver les valeurs de m et c durant la procédure d’ajustement. Si nous trouvions m = 0,5 et c = 37, nous obtiendrions la visualisation suivante :
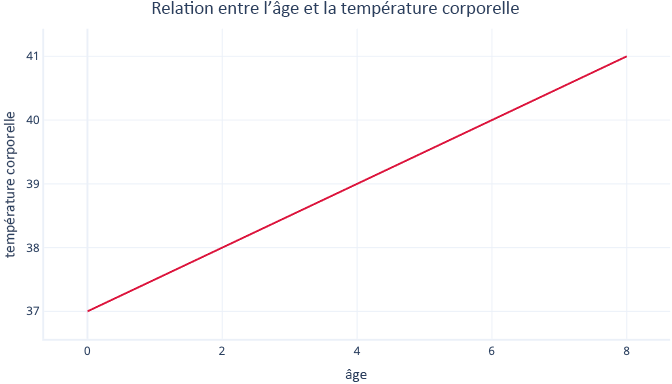
Cela signifierait que chaque année d'âge est associée à une augmentation de la température corporelle de 0,5°C, avec un point de départ de 37°C.
Ajustement de la régression linéaire
En règle générale, nous utilisons des bibliothèques existantes pour ajuster les modèles de régression. La régression vise généralement à trouver la ligne qui produit le moins d’erreurs. Le terme « erreur » signifie ici la différence entre la valeur réelle du point de données et la valeur prédite. Par exemple, dans l’image suivante, la ligne noire indique l’erreur entre la prédiction, la ligne rouge et une valeur réelle, le point.
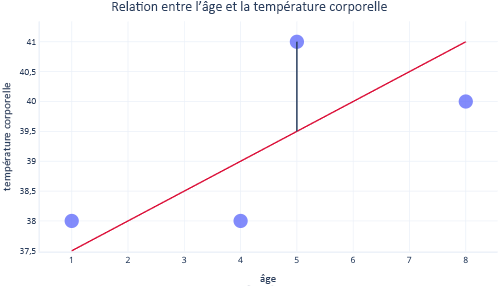
En observant ces deux points sur l'axe des ordonnées, nous pouvons voir que la prédiction était de 39,5, mais que la valeur réelle était de 41.
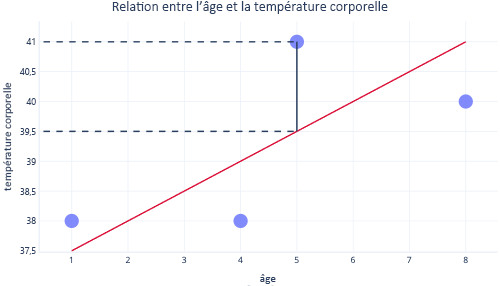
Par conséquent, le modèle présentait une erreur de 1,5 pour ce point de données.
Le plus souvent, nous ajustons un modèle en minimisant la somme résiduelle de carrés. Cela signifie que la fonction de coût est calculée comme suit :
- Calcul de la différence entre les valeurs réelles et prédites (comme ci-dessus) pour chaque point de données.
- Élévation de ces valeurs au carré.
- Somme (ou moyenne) de ces valeurs au carré.
Cette étape d’élévation au carré signifie que tous les points ne contribuent pas de manière égale à la ligne : les valeurs hors norme, qui sont des points non conformes au modèle attendu, présentent une erreur beaucoup plus importante, ce qui peut influencer la position de la ligne.
Points forts de la régression
Les techniques de régression présentent de nombreux atouts que n'ont pas les modèles plus complexes.
Prévisibles et faciles à interpréter
Les régressions sont faciles à interpréter car elles correspondent à des équations mathématiques simples, que nous pouvons souvent représenter graphiquement. Les modèles plus complexes sont souvent qualifiés de solutions de type boîte noire, car il est difficile de comprendre la façon dont ils effectuent les prédictions ou la façon dont ils se comportent avec certaines entrées.
Extrapolation aisée
Les régressions facilitent l’extrapolation, en d’autres termes, la génération de prédictions pour les valeurs situées en dehors de la plage de notre jeu de données. Ainsi, dans notre exemple précédent, on peut facilement estimer qu’un chien de neuf ans aura une température de 40,5 °C. Vous devez toujours faire preuve de prudence en ce qui concerne l’extrapolation : ce modèle prédit qu’une personne de 90 ans aura une température quasiment équivalente à celle du point d’ébullition de l’eau.
Un ajustement optimal est généralement garanti
La plupart des modèles Machine Learning utilisent la Descente de Gradient pour optimiser les modèles, ce qui implique d'ajuster l'algorithme de la Descente de Gradient et ne garantit pas qu'une solution optimale sera trouvée. En revanche, la régression linéaire qui utilise la somme des carrés en tant que fonction de coût ne nécessite pas de procédure itérative telle que la descente de gradient. Au lieu de cela, des calculs mathématiques astucieux peuvent être utilisés pour déterminer l'emplacement optimal de la droite à placer. Ces calculs mathématiques sortent du cadre de ce module. Toutefois, sachez que (tant que la taille de l’échantillon n’est pas trop grande) la régression linéaire ne nécessite pas d’attention particulière pour le processus d’ajustement, et qu’une solution optimale est garantie.