Évaluation d’un modèle de classification

4 minutes

L’apprentissage automatique consiste principalement à évaluer le fonctionnement des modèles. Cette évaluation a lieu au cours de l’apprentissage, pour faciliter la mise en forme du modèle, et après l’apprentissage, pour nous aider à juger si le modèle est utilisable dans le monde réel. Les modèles de classification doivent être évalués, tout comme les modèles de régression, même si la manière dont nous procédons à cette évaluation peut parfois être un peu plus complexe.

Rappel sur les coûts

Rappelez-vous que, pendant l’apprentissage, nous calculons le niveau de performance d’un modèle, que nous appelons coût ou perte. Par exemple, dans la régression linéaire, nous utilisons souvent une métrique appelée erreur carrée moyenne (MSE). La MSE est calculée en comparant l’étiquette prédite et l’étiquette réelle, en élevant la différence au carré et en prenant la moyenne du résultat. Nous pouvons utiliser la MSE pour ajuster notre modèle et rendre compte de son efficacité.

Fonctions de coût pour la classification

Les modèles de classification sont jugés d’après les probabilités en sortie, comme 40 % de risques d’avalanche, ou d’après leurs étiquettes finales – no avalanche ou avalanche. L’utilisation des probabilités de sortie peut être avantageuse pendant l’entraînement. Les légères modifications du modèle affectent les probabilités, même si elles ne suffisent pas à modifier la décision finale. L’utilisation des étiquettes finales d’une fonction de coût est plus utile si nous souhaitons estimer les performances réelles de notre modèle. Par exemple, sur le jeu de test. En effet, pour une utilisation réelle, nous utilisons les étiquettes finales, et non les probabilités.

Perte du journal

La perte logarithmique est l’une des fonctions de coût les plus populaires pour la classification simple. La perte logarithmique est appliquée aux probabilités de sortie. Comme pour l’erreur carrée moyenne, de faibles quantités d’erreurs entraînent un faible coût, tandis que des quantités modérées d’erreurs entraînent des coûts importants. Nous avons produit un tracé de la perte logarithmique dans le graphique suivant pour une étiquette où la réponse correcte était 0 (false).

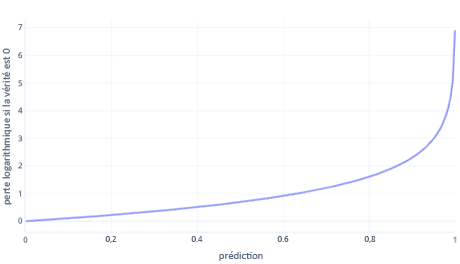
Diagramme représentant un exemple de graphique de perte logarithmique.

L’axe des x montre les sorties possibles du modèle (des probabilités de 0 à 1) et l’axe des y le coût. Si un modèle est tout à fait sûr que la réponse correcte est 0 (par exemple en prédisant 0,1), le coût est faible, car dans ce cas la réponse correcte est 0. Si le modèle est sûr de prédire le résultat de manière erronée (par exemple, en prédisant 0,9), le coût devient élevé. En fait, en x=1, le coût est si élevé que nous rognons ici l’axe des x à 0,999 pour que le graphique reste lisible.

Pourquoi pas l’erreur carrée moyenne ?

La valeur et la perte logarithmique sont des mesures similaires. La perte logarithmique est privilégiée à la régression logistique pour certaines situations complexes mais aussi des situations plus simples. Par exemple, la perte logarithmique pénalise les mauvaises réponses beaucoup plus fortement que l’erreur carrée moyenne. Ainsi, dans le graphique suivant, où la réponse correcte est 0, les prédictions supérieures à 0,8 ont un coût plus élevé pour la perte logarithmique que pour la valeur de MSE.

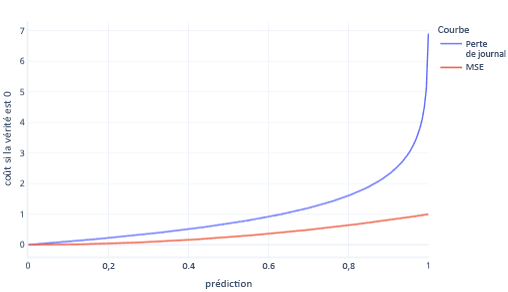
Diagramme représentant une perte logarithmique par rapport à une erreur carrée moyenne.

Le fait d’avoir un coût plus élevé de cette manière aide le modèle à apprendre plus rapidement car la pente de la ligne est plus forte. De même, la perte logarithmique garantit une meilleure probabilité que les modèles donnent la bonne réponse. Remarquez dans le graphique ci-dessus que le coût MSE pour les valeurs inférieures à 0,2 est faible et que la pente est presque plate. Cette relation ralentit l’apprentissage pour les modèles qui sont presque corrects. La perte logarithmique a une pente plus forte pour ces valeurs, ce qui aide le modèle à apprendre plus rapidement.

Limites des fonctions de coût

L’utilisation d’une seule fonction de coût pour l’évaluation humaine du modèle est toujours limitée car elle ne vous indique pas le type d’erreur commis par votre modèle. Par exemple, considérons notre scénario de prévision des avalanches. Une valeur élevée de perte logarithmique pourrait signifier que le modèle prédit de manière répétée des avalanches alors qu’il n’y en a pas. Ou cela peut signifier qu’il ne parvient pas à prédire à plusieurs reprises les avalanches qui se produisent.