Qu’est-ce que la régression ?
La régression fonctionne en établissant une relation entre des variables dans les données qui représentent des caractéristiques de l’élément observé, et la variable que nous essayons de prédire, appelée étiquette.
Rappel : Notre entreprise loue des bicyclettes et veut prédire le nombre de locations attendues pour un jour donné. Dans ce cas, les caractéristiques incluent des éléments comme le jour de la semaine, le mois, etc., et l’étiquette est le nombre de locations de vélos.
Pour effectuer la formation du modèle, nous commençons par un exemple de données contenant des caractéristiques, ainsi que des valeurs connues pour l’étiquette. Ici, nous avons donc besoin de données d’historique contenant les dates, les conditions météorologiques et le nombre de locations de vélos.
Nous allons ensuite fractionner cet exemple de données en deux sous-ensembles :
- Un jeu de données d’apprentissage auquel nous allons appliquer un algorithme qui détermine une fonction encapsulant la relation entre les valeurs de fonctionnalité et les valeurs d’étiquette connues.
- Un jeu de données de validation ou de test que nous pouvons utiliser pour évaluer le modèle en l’utilisant pour générer des prédictions pour l’étiquette et en les comparant aux valeurs d’étiquette connues réelles.
L’utilisation de données historiques avec des valeurs d’étiquette connues pour effectuer l’apprentissage d’un modèle fait de la régression un exemple d’apprentissage automatique supervisé.
Un exemple simple
Prenons un exemple simple pour voir le fonctionnement théorique du processus d’apprentissage et d’évaluation. Supposons que nous simplifions le scénario de manière à n’utiliser qu’une seule caractéristique, la température journalière moyenne, pour prédire l’étiquette de locations de vélos.
Nous commençons avec des données qui incluent des valeurs connues pour la fonctionnalité de température quotidienne moyenne et l’étiquette de locations de vélos.
| Température | Locations |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
À présent, nous allons sélectionner aléatoirement cinq de ces observations et les utiliser pour entraîner un modèle de régression. Quand nous parlons « d’entraîner un modèle », nous voulons dire trouver une fonction (une équation mathématique, appelons-la f) qui peut utiliser la caractéristique « température » (que nous appelons x) pour calculer le nombre de locations (que nous appelons y). En d’autres termes, nous devons définir la fonction suivante : f(x) = y.
Notre jeu de données d’apprentissage se présente comme suit :
| x | y |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
Commençons par tracer les valeurs d’apprentissage pour x et y sur un graphique :
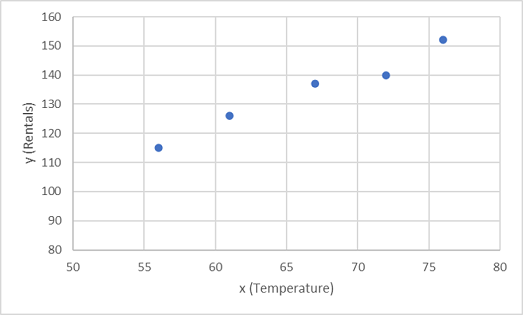
Nous devons à présent ajuster ces valeurs à une fonction, autorisant ainsi une variation aléatoire. Vous pouvez probablement constater que les points tracés forment une ligne diagonale presque droite. En d’autres termes, il existe une relation linéaire apparente entre x et y. Nous devons donc trouver une fonction linéaire qui correspond le mieux à l’exemple de données. Il existe différents algorithmes que nous pouvons utiliser pour déterminer cette fonction, pour trouver au final une ligne droite avec une variance globale minimale des points tracés semblable à ceci :
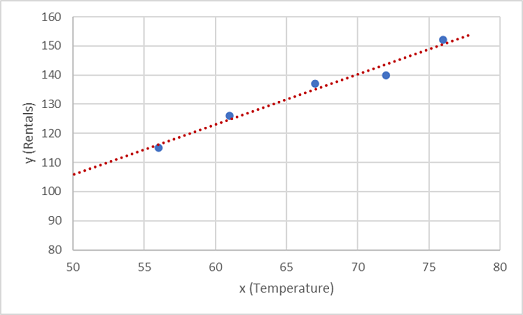
La ligne représente une fonction linéaire qui peut être utilisée avec n’importe quelle valeur de x pour appliquer la pente de la ligne et son point d’intersection (où la ligne croise l’axe y quand x est égal à 0) pour calculer y. Dans ce cas, si nous avions étendu la ligne à gauche, nous aurions constaté que lorsque x est égal à 0, y est d’environ 20 et la pente de la ligne est telle que, pour chaque unité de x que vous déplacez vers la droite, y augmente d’environ 1,7. Nous pouvons donc calculer notre fonction f comme 20 + 1,7x.
Maintenant que nous avons défini notre fonction prédictive, nous pouvons l’utiliser pour prédire des étiquettes pour les données de validation que nous avons conservées et comparer les valeurs prédites (que nous indiquons généralement par le symbole ŷ, ou « y-hat ») avec les valeurs de y connues réelles.
| x | y | ŷ |
|---|---|---|
| 82 | 156 | 159,4 |
| 54 | 114 | 111,8 |
| 62 | 129 | 125,4 |
Examinons les valeurs de y et ŷ en comparaison dans un tracé :
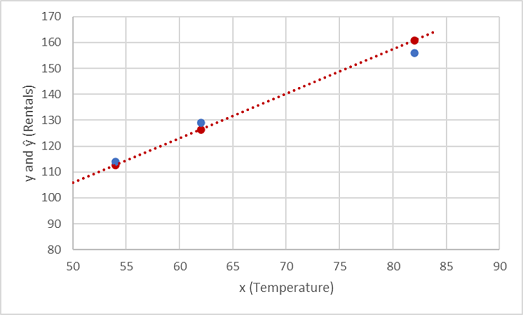
Les points tracés sur la ligne de la fonction correspondent aux valeurs de ŷ prédites calculées par la fonction, tandis que les autres points tracés sont les valeurs réelles de y.
Il existe plusieurs façons de mesurer la variance entre les valeurs prédites et réelles, et nous pouvons utiliser ces métriques pour évaluer le degré de prédiction du modèle.
Notes
L’apprentissage automatique est basé sur des statistiques et des mathématiques, et il est important de connaître les termes spécifiques utilisés par les statisticiens et les mathématiciens (et par conséquent les scientifiques de données). Vous pouvez considérer que la différence entre une valeur d’étiquette prédite et la valeur d’étiquette réelle comme la mesure de l’erreur. Toutefois, dans la pratique, les valeurs « réelles » sont basées sur des observations d’échantillons (qui peuvent elles-mêmes être sujettes à un certain écart aléatoire). Pour clarifier le fait que nous comparons une valeur prédite (ŷ) à une valeur observée (y) , nous appelons la différence entre elles les valeurs résiduelles. Nous pouvons faire la somme des valeurs résiduelles de toutes les prédictions des données de validation afin de calculer la perte globale dans le modèle comme mesure de sa performance prédictive.
L’une des méthodes les plus courantes pour mesurer la perte consiste à calculer le carré des valeurs résiduelles individuelles, à additionner les carrés et à calculer la moyenne. Le calcul du carré des valeurs résiduelles a comme effet de baser le calcul sur des valeurs absolues (en ignorant le fait que la différence est négative ou positive) et donne plus de poids aux différences plus grandes. Cette métrique est appelée l’erreur carrée moyenne.
Pour nos données de validation, le calcul se présente comme suit :
| y | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159,4 | -3,4 | 11,56 |
| 114 | 111,8 | 2.2 | 4,84 |
| 129 | 125,4 | 3.6 | 12,96 |
| Sum | ∑ | 29,36 | |
| Moyenne | x̄ | 9,79 |
La perte de notre modèle basé sur la métrique MSE est donc de 9,79.
Est-ce correct ? C’est difficile à dire, car la valeur de l’erreur carrée moyenne n’est pas exprimée dans une unité de mesure significative. Nous savons que plus la valeur est faible, plus la perte est faible dans le modèle et, par conséquent, meilleure est la prédiction. Cela en fait une métrique utile pour comparer deux modèles et trouver le plus performant.
Il est parfois plus utile d’exprimer la perte dans la même unité de mesure que la valeur de l’étiquette prédite (ici, le nombre de locations). Il est possible de faire cela en calculant la racine carrée de l’erreur quadratique moyenne, ce qui donne une métrique connue sous le nom de racine de l’erreur quadratique moyenne (RMSE).
√9,79 = 3,13
L’erreur quadratique moyenne de notre modèle indique ainsi que la perte est tout juste supérieure à 3, ce que vous pouvez interpréter comme signifiant des prédictions erronées en moyenne d’environ trois locations.
De nombreuses autres métriques peuvent être utilisées pour mesurer la perte dans une régression. Par exemple, R2 (R carré) (parfois appelé coefficient de détermination) est la corrélation entre x et y au carré. Cela produit une valeur comprise entre 0 et 1 qui mesure la quantité de variance pouvant être expliquée par le modèle. En règle générale, plus cette valeur est proche de 1, meilleure sera la prédiction du modèle.