Concepts du réseau neuronal profond

Effectué

Avant d’étudier comment former un modèle de Machine Learning DNN (Deep neuronal Network), examinons ce que nous essayons d’atteindre. Le Machine Learning concerne la prédiction d’une étiquette en fonction de certaines fonctionnalités d’une observation particulière. En termes simples, un modèle de Machine Learning est une fonction qui calcule y (l’étiquette) à partir de x (les caractéristiques) : f(x)=y.

Exemple de classification simple

Supposons, par exemple, que votre observation se compose de mesures d’un manchot.

Plus précisément, les mesures sont les suivantes :

• La longueur du bec du manchot.
• La profondeur du bec du manchot.
• La longueur de la nageoire du manchot.
• Le poids du manchot.

Dans ce cas, les caractéristiques (x) sont un vecteur de quatre valeurs, ou mathématiquement, x=[x₁,x₂,x₃,x₄].

Supposons que l’étiquette que nous essayons de prédire (y) soit l’espèce du manchot et qu’il y ait trois espèces possibles :

0. Adélie
1. Manchot papou
2. Manchot à jugulaire

Il s’agit d’un exemple de problème de classification dans lequel le modèle de machine learning doit prédire la classe la plus probable à laquelle l’observation appartient. Un modèle de classification effectue cela en prédisant une étiquette qui se compose de la probabilité pour chaque classe. En d’autres termes, y est un vecteur de trois valeurs de probabilité, une pour chacune des classes possibles : y=[P(0),P(1),P(2)].

Vous pouvez former le modèle de Machine Learning à l’aide d’observations pour lesquelles vous connaissez déjà la véritable étiquette. Par exemple, vous pouvez avoir les mesures de fonctionnalités suivantes pour un spécimen Adélie :

x=[37,3, 16,8, 19,2, 30,0]

Vous savez déjà qu’il s’agit d’un exemple de type Adélie (classe 0). Par conséquent, une fonction de classification parfaite doit générer une étiquette qui indique une probabilité de 100 % pour la classe 0 et une probabilité de 0 % pour les classes 1 et 2 :

y=[1, 0, 0]

Un modèle de réseau neuronal profond

Donc, comment pouvons-nous utiliser le Deep Learning pour créer un modèle de classification pour le modèle de classification des manchots ? Prenons un exemple :

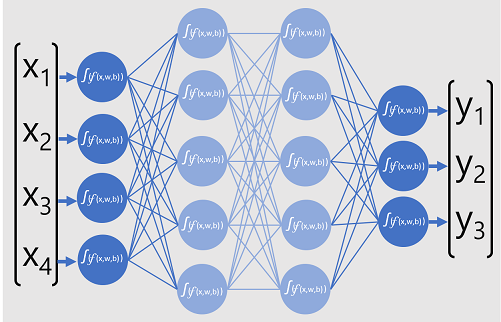
Le modèle de réseau neuronal profond pour le classifieur est constitué de plusieurs couches de neurones artificiels. Dans cet exemple, il y en a quatre :

• Couche d’entrée avec un neurone pour chaque valeur d’entrée (x) attendue.
• Deux couches cachées, appelées couches masquées , chacune contenant cinq neurones.
• Couche de sortie contenant trois neurones : un pour chaque valeur de probabilité de classe (y) devant être prédite par le modèle.

En raison de l’architecture en couches du réseau, ce type de modèle est parfois appelé Perceptron multicouche. En outre, Notez que tous les neurones des couches d’entrée et masquées sont connectés à tous les neurones des couches suivantes : il s’agit d’un exemple de réseau entièrement connecté.

Lorsque vous créez un modèle comme celui-ci, vous devez définir une couche d’entrée qui prend en charge le nombre de fonctionnalités que votre modèle traitera, et une couche de sortie qui reflète le nombre de sorties que vous prévoyez de produire. Vous pouvez choisir le nombre de couches masquées que vous souhaitez inclure et le nombre de neurones dans chacun d’eux. Mais vous n’avez aucun contrôle sur les valeurs d’entrée et de sortie pour ces couches. Celles-ci sont déterminées par le processus d’apprentissage du modèle.

Apprentissage d’un réseau neuronal profond

Le processus d’apprentissage d’un réseau neuronal profond est constitué de plusieurs itérations, appelées époques. Pour la première époque, vous commencez par assigner des valeurs d’initialisation aléatoires pour les valeurs poids (w) et biais b. Le processus est alors le suivant :

1. Les fonctionnalités pour les observations de données avec des valeurs d’étiquette connues sont soumises à la couche d’entrée. En règle générale, ces observations sont regroupées en lots (souvent appelés mini-lots).
2. Les neurones appliquent ensuite leur fonction et, s’ils sont activés, passent le résultat sur la couche suivante jusqu’à ce que la couche de sortie génère une prédiction.
3. La prédiction est comparée à la valeur connue réelle, et la quantité d’écart entre les valeurs prédites et vraies (que nous appelons la perte) est calculée.
4. En fonction des résultats, les valeurs révisées pour les valeurs de poids et de biais sont calculées pour réduire la perte, et ces ajustements sont propagés vers les neurones dans les couches réseau.
5. L’époque suivante répète la passe de formation par lot avec les valeurs de poids et de biais révisées, en améliorant l’exactitude du modèle (en réduisant la perte).

Notes

Le traitement des fonctionnalités de formation en tant que lot améliore l’efficacité du processus de formation en traitant plusieurs observations simultanément sous la forme d’une matrice de caractéristiques avec des vecteurs de poids et de biais. Les fonctions algébriques linéaires qui exploitent les matrices et les vecteurs sont également intégrées au traitement graphique 3D, c’est pourquoi les ordinateurs dotés d’unités de traitement graphique (GPU) offrent de meilleures performances pour l’apprentissage du modèle Deep Learning que les ordinateurs à processeurs uniquement.

Présentation détaillée des fonctions de perte et de la rétropropagation

La description précédente du processus d’apprentissage approfondi a mentionné que la perte du modèle est calculée et utilisée pour ajuster les valeurs de poids et de biais. Comment ceci fonctionne-t-il ?

Calcul de la perte

Supposons que l’un des exemples passés par le processus d’apprentissage contient les fonctionnalités d’un spécimen Adélie (classe 0). La sortie correcte du réseau serait [1, 0, 0]. Supposons à présent que la sortie produite par le réseau soit [0,4, 0,3, 0,3]. En comparant ceux-ci, nous pouvons calculer une variance absolue pour chaque élément (en d’autres termes, la part de chaque valeur prédite à partir de ce qu’elle devrait être) en tant que [0,6, 0,3, 0,3].

En réalité, étant donné que nous sommes en train de traiter plusieurs observations, nous regroupons généralement la variance. Par exemple, en élevant au carré les valeurs de variance individuelles et en calculant la moyenne, nous recherchons une valeur de perte moyenne unique, comme 0,18.

Optimiseurs

Voici maintenant l’astuce. La perte est calculée à l’aide d’une fonction, qui opère sur les résultats de la couche finale du réseau, qui est également une fonction. La couche finale du réseau opère sur les sorties des couches précédentes, qui sont également des fonctions. En effet, l’ensemble du modèle de la couche d’entrée directement dans le calcul de la perte n’est qu’une seule fonction volumineuse imbriquée. Les fonctions ont quelques caractéristiques vraiment utiles, notamment :

• Vous pouvez conceptualiser une fonction comme une ligne tracée en comparant sa sortie à chacune de ses variables.
• Vous pouvez utiliser le calcul différentiel pour calculer la dérivée de la fonction à tout moment par rapport à ses variables.

Prenons la première de ces fonctionnalités. Nous pouvons tracer la ligne de la fonction pour montrer comment une valeur de pondération individuelle est comparée à la perte et marquer sur cette ligne le point où la valeur de poids actuelle correspond à la valeur de perte actuelle.

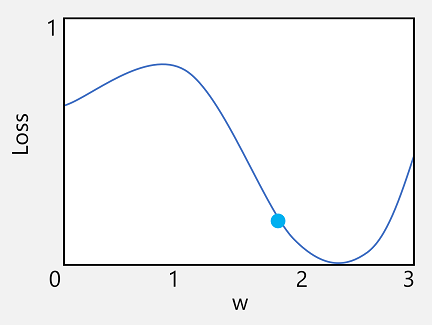
À présent, nous allons appliquer la deuxième caractéristique d’une fonction. La dérivée d’une fonction pour un point donné indique si la pente (ou le dégradé) de la sortie de la fonction (dans ce cas, la perte) est augmentée ou diminuée par rapport à une variable de fonction (dans ce cas, la valeur de poids). Un dérivé positif indique que la fonction est en augmentation, et une dérivée négative indique qu’elle diminue. Dans ce cas, au point tracé pour la valeur de poids actuelle, la fonction a un dégradé vers le bas. En d’autres termes, l’augmentation du poids aura pour effet de réduire la perte.

Nous utilisons un optimiseur pour appliquer cette même astuce pour toutes les variables de poids et de biais dans le modèle et déterminer dans quelle direction nous devons les ajuster (haut ou bas) pour réduire la quantité totale de perte dans le modèle. Il existe plusieurs algorithmes d’optimisation couramment utilisés, y compris la descente de gradient stochastique (SGD), le taux d’apprentissage adaptatif (ADADELTA), l’évaluation de la dynamique adaptative (Adam), et d’autres ; tous sont conçus pour déterminer comment ajuster les poids et les biais pour réduire la perte.

Taux d’apprentissage

À présent, la question suivante évidente est, d’après combien de temps l’optimiseur ajuste-t-il les valeurs de poids et de biais ? Si vous examinez le tracé de notre valeur de poids, vous pouvez constater que l’augmentation de la pondération d’une petite quantité suit la ligne de fonction vers le haut (ce qui réduit la perte), mais si nous l’augmentons trop rapidement, la ligne de fonction recommence à s’afficher, ce qui peut entraîner une augmentation de la perte ; après l’époque suivante, nous pourrions avoir besoin de réduire le poids.

La taille de l’ajustement est contrôlée par un paramètre que vous définissez pour l’apprentissage, appelé taux d’apprentissage. Un faible taux d’apprentissage entraîne des ajustements minimes (par conséquent, il peut prendre plus d’époques pour réduire la perte), tandis qu’un taux d’apprentissage élevé entraîne des ajustements importants (vous risquez donc de manquer le minimum).