Évaluer les différents types de clustering

Effectué

Apprentissage d'un modèle de clustering

Il existe plusieurs algorithmes que vous pouvez utiliser pour le clustering. L’un des algorithmes les plus couramment utilisés est le clustering K-Means, qui, dans sa forme la plus simple, comprend les étapes suivantes :

1. Les valeurs de caractéristique sont vectorisées pour définir des coordonnées à n dimensions (où n est le nombre de caractéristiques). L’exemple de fleur comprend deux caractéristiques : le nombre de pétales et le nombre de feuilles. Le vecteur de caractéristique a donc deux coordonnées que nous pouvons utiliser pour tracer de manière conceptuelle les points de données dans un espace à deux dimensions.
2. Vous devez déterminer le nombre de clusters à utiliser pour regrouper les fleurs. Appelez cette valeur k. Par exemple, pour créer trois clusters, vous devez utiliser une valeur k de 3. Ensuite, les points k sont tracés sur des coordonnées aléatoires. Ces points deviennent les points centraux de chaque cluster et sont donc appelés centroïdes.
3. Chaque point de données (chaque fleur, dans ce cas) est attribué à son centroïde le plus proche.
4. Chaque centroïde est déplacé vers le centre des points de données qui lui sont attribués en fonction de la distance moyenne entre les points.
5. Après le déploiement du centroïde, les points de données peuvent se rapprocher d’un autre centroïde. Les points de données sont donc réattribués aux clusters en fonction du centroïde le plus proche.
6. Les étapes de déplacement du centroïde et de réattribution de cluster se répètent jusqu’à ce que les clusters deviennent stables ou qu’un nombre maximal d’itérations prédéterminé soit atteint.

L’animation suivante illustre ce processus :

Clustering hiérarchique

Le clustering hiérarchique est un autre type d’algorithme de clustering dans lequel les clusters appartiennent à des groupes plus grands, eux-mêmes appartenant à des groupes encore plus grands, etc. Il en résulte que les points de données peuvent être des clusters avec des degrés de précision différents : avec un grand nombre de groupes très petits et précis, ou un petit nombre de groupes de plus grande taille.

Par exemple, si nous appliquons un clustering aux significations des mots, nous pouvons obtenir un groupe contenant des adjectifs spécifiques aux émotions (en colère, heureux, etc.). Ce groupe fait partie d’un groupe contenant tous les adjectifs liés à l’être humain (« heureux », « beau », « jeune »), lui-même appartenant à un groupe encore plus élevé contenant tous les adjectifs (« heureux », « vert », « beau », « dur », etc.).

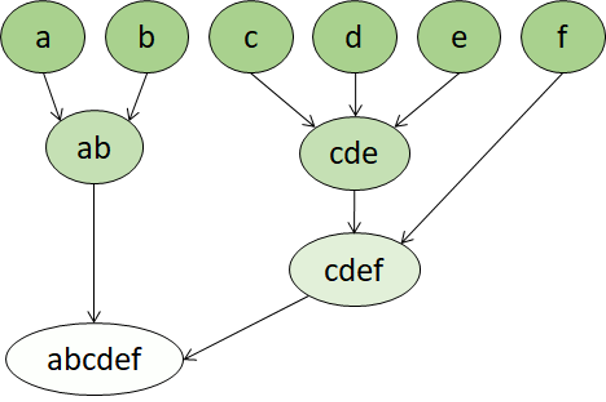
Le clustering hiérarchique permet non seulement de fractionner les données en groupes, mais aussi de comprendre les relations entre ces groupes. L’un des principaux avantages du clustering hiérarchique est qu’il ne nécessite pas de définir le nombre de clusters à l’avance. En outre, cette méthode peut parfois fournir des résultats plus interprétables que les approches non hiérarchiques. Le principal inconvénient est que le calcul de ces approches peut durer plus longtemps que pour les approches plus simples, et qu’elles ne sont parfois pas adaptées aux grands jeux de données.