Qu’est-ce que la classification ?
La classification binaire est la classification avec deux catégories. Par exemple, nous pouvons étiqueter les patients comme non-diabétiques ou diabétiques.
La prédiction de classe est effectuée en déterminant la probabilité pour chaque classe possible comme une valeur comprise entre 0 (impossible) et 1 (certain). La probabilité totale pour toutes les classes est toujours 1, car le patient est définitivement diabétique ou non diabétique. Par conséquent, si la probabilité prédite qu’un patient soit diabétique est de 0,3, il existe une probabilité correspondante de 0,7 que le patient soit non diabétique.
Une valeur de seuil, souvent 0,5, est utilisée pour déterminer la classe prédite. Si la classe positive (dans notre exemple, diabétique) a une probabilité prédite supérieure au seuil, une classification « diabétique » est prédite.
Apprentissage et évaluation d’un modèle de classification
La classification est un exemple de technique de machine learning supervisée, ce qui signifie qu’elle s’appuie sur des données qui comprennent des valeurs de caractéristiques connues et des valeurs d’étiquettes connues. Dans cet exemple, les valeurs de caractéristiques sont des mesures de diagnostic pour des patients, et les valeurs d’étiquettes correspondent à une classification en non diabétique ou diabétique. Un algorithme de classification est utilisé pour faire correspondre un sous-ensemble des données à une fonction qui peut calculer la probabilité pour chaque étiquette de classe à partir des valeurs des caractéristiques. Les données restantes sont utilisées pour évaluer le modèle en comparant les prédictions qu’il génère des caractéristiques aux étiquettes de classe connues.
Un exemple simple
Explorons un exemple pour expliquer les principes clés. Supposons que nous avons les données de patients suivantes, qui se composent d’une seule caractéristique (le niveau de glycémie) et d’une étiquette de classe : 0 pour non diabétique, 1 pour diabétique.
| Glycémie | Diabétique |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
Nous utilisons les huit premières observations pour entraîner un modèle de classification, et nous commençons par tracer la caractéristique glycémie (x) et l’étiquette « diabétique » prédite (y).
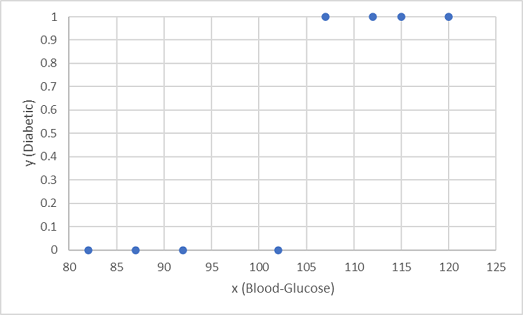
Nous avons besoin d’une fonction qui calcule une valeur de probabilité pour y en fonction de x (en d’autres termes, nous avons besoin de la fonction f(x) = y). Vous pouvez voir à partir du graphique que les patients dont le niveau de glycémie est faible sont tous non-diabétiques, tandis que les patients dont le niveau de glycémie est plus élevé sont diabétiques. Il apparaît que plus le niveau de glycémie est élevé, plus il est probable qu’un patient est diabétique, le point d’inflexion étant quelque part entre 100 et 110. Nous devons ajuster une fonction qui calcule une valeur comprise entre 0 et 1 pour y à ces valeurs.
Une fonction de ce type est une fonction logistique, qui forme une courbe sigmoïde (en forme de S).
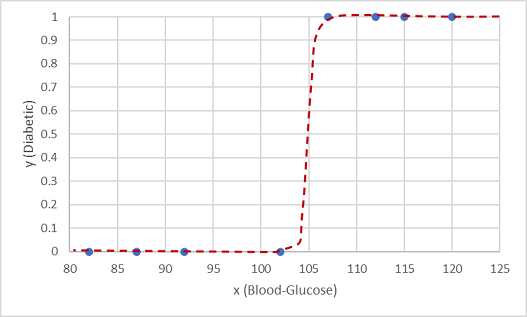
Nous pouvons maintenant utiliser la fonction pour calculer une valeur de probabilité que y soit positif, ce qui signifie que le patient est diabétique, à partir de n’importe quelle valeur de x en recherchant le point sur la ligne de caractéristique pour x. Nous pouvons définir une valeur de seuil de 0,5 comme point de coupure pour la prédiction de l’étiquette de la classe.
Testons-la avec les deux valeurs de données que nous avons retenues.
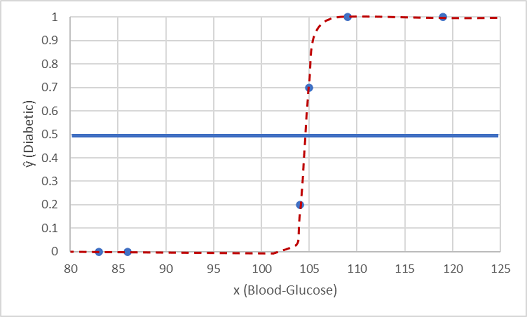
Les points tracés sous la ligne du seuil vont produire une classe prédite de 0 (non diabétique) et les points au-dessus de la ligne seront prédites comme étant 1 (diabétique).
Nous pouvons à présent comparer les prédictions d’étiquette (ŷ ou « y chapeau ») effectuées d’après la fonction logistique encapsulée dans le modèle aux étiquettes de classe réelles (y).
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |