Normalisation et standardisation
La mise à l’échelle des caractéristiques est une technique qui modifie la plage de valeurs d’une caractéristique. Elles aident les modèles à apprendre plus rapidement et de manière plus robuste.
La différence entre normalisation et standardisation
La normalisation signifie que les valeurs sont mises à l’échelle de façon à entrer dans une certaine plage, comprise en général entre 0 et 1. Supposons par exemple que vous disposiez d’une liste de personnes âgées de 0, 50 et 100 ans. Vous pouvez la normaliser en divisant les âges par 100, de sorte que vos valeurs deviennent 0, 0,5 et 1.
La standardisation est similaire, à ceci près qu’elle soustrait la moyenne des valeurs, puis divise le résultat par l’écart type. Si vous ne connaissez pas le concept d’écart type, ne vous inquiétez pas. Cela signifie que, après standardisation, notre valeur moyenne est égale à zéro, et qu’environ 95 % des valeurs sont comprises entre -2 et 2.
Il existe d’autres façons de mettre à l’échelle les données, mais elles présentent des nuances qui dépassent ce que nous avons besoin de savoir pour le moment. Voyons pourquoi appliquer la normalisation ou la standardisation.
Pourquoi avons-nous besoin d’une mise à l’échelle ?
De nombreuses raisons justifient de normaliser ou de standardiser les données avant l’apprentissage. Vous pouvez les comprendre plus facilement avec un exemple. Supposons que nous souhaitions effectuer l’apprentissage d’un modèle pour prédire si un chien sera performant dans la neige. Nos données apparaissent dans le graphique ci-dessous sous forme de points. La courbe de tendance que nous essayons de trouver se présente comme une droite pleine :
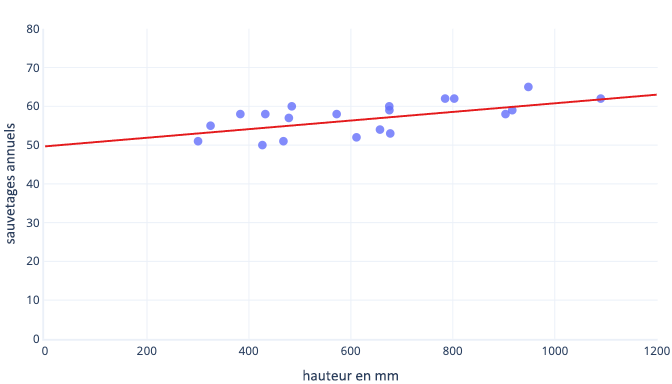
Un meilleur point de départ pour l’apprentissage
La ligne optimale du graphique précédent présente deux paramètres : le point d’intersection, 50 (la ligne à x = 0) et la pente, 0,01, les sauvetages augmentent de 10 tous les 1 000 millimètres. Supposons que nous commencions l’apprentissage avec une estimation initiale de 0 pour ces deux paramètres.
Si nos itérations de formation modifient les paramètres d’environ 0,01 en moyenne par itération, il faut au moins 5 000 itérations (50/0,01) pour trouver le point d’intersection. La standardisation permet de ramener ce point d’intersection optimal plus près de zéro, et donc de le trouver beaucoup plus rapidement. Par exemple, si l’on soustrait la moyenne de notre étiquette (le nombre de sauvetages annuels) et de notre caractéristique (la taille), le point d’intersection est -0,5, et non 50. On peut donc le trouver environ 100 fois plus vite.
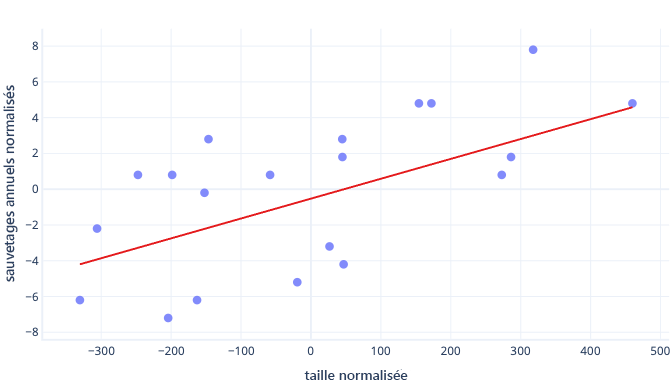
Il existe d’autres raisons pour lesquelles l’apprentissage des modèles complexes peut se révéler très lent lorsque l’estimation initiale se trouve loin du compte, mais la solution reste toujours la même : décaler les caractéristiques de façon à les rapprocher de l’estimation initiale.
La même vitesse d’entraînement des paramètres
Les données présentent maintenant un décalage idéal de -0,5 et une pente idéale de 0,01. Bien que ce décalage permette d’accélérer les choses, sa formation reste beaucoup plus lente que celle de la pente. Cela risque de la rendre longue et instable.
Dans notre exemple, les hypothèses initiales sont égales à zéro pour le décalage et la pente. Modifier les paramètres d’environ 0,1 à chaque itération permet de trouver rapidement le décalage. Il est cependant très difficile de détecter la bonne pente, car elle augmente trop vite (0+0,1 > 0,01) et risque de dépasser la valeur idéale. Or, réduire les ajustements aurait pour effet de ralentir la recherche du point d’intersection.
Que se passe-t-il si l’on met à l’échelle la caractéristique de taille ?
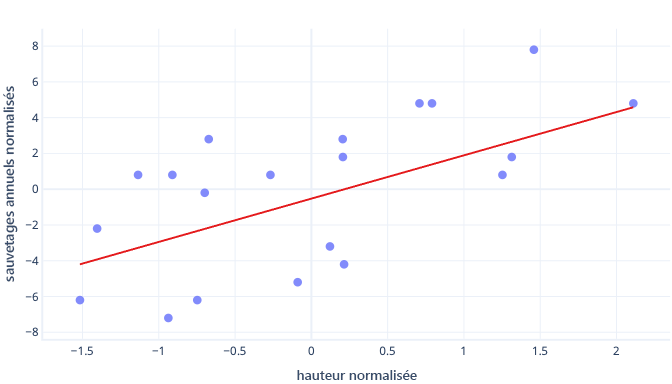
La pente de la droite devient 0,5. Regardez bien l’axe X. Le point d’intersection optimal de -0,5 et la pente de 0,5 présentent la même échelle ! Il est maintenant facile de choisir une taille de pas raisonnable, qui correspond à la vitesse à laquelle la descente de gradient met à jour les paramètres.
L’utilisation de plusieurs caractéristiques
Lorsque l’on travaille avec de nombreuses caractéristiques, leur mise à l’échelle peut entraîner des problèmes d’ajustement, comme avec les cas précédents de point d’intersection et de pente. Prenons l’exemple de l’apprentissage d’un modèle qui accepte à la fois la taille en mm et le poids en tonnes. De nombreux types de modèles ont du mal à apprécier l’importance de la caractéristique de poids, simplement parce qu’elle est petite par rapport aux caractéristiques de taille.
Dois-je toujours effectuer une mise à l’échelle ?
Il n’est pas toujours nécessaire de mettre à l’échelle. Certains types de modèles, notamment les modèles précédents avec des lignes droites, peuvent être ajustés sans procédure itérative comme une descente de gradient. Que les caractéristiques ne soient pas de la bonne taille ne constitue donc pas un problème. D’autres modèles ont besoin d’une mise à l’échelle pour que l’entraînement soit correct, mais leurs bibliothèques effectuent souvent une mise à l’échelle automatique des caractéristiques.
En règle générale, les seuls inconvénients réels de la normalisation ou de la standardisation sont qu’elles peuvent compliquer l’interprétation des modèles et obliger à écrire un peu plus de code. C’est la raison pour laquelle la mise à l’échelle des caractéristiques constitue une partie standard de la création de modèles Machine Learning.